円に内接する四角形

円に内接する四角形と対角線の長さ
問題解説：円に内接する四角形
今回のまとめ

円に内接する四角形と対角線の長さ

Point：円に内接する四角形円に内接する四角形 ${\rm ABCD}$ において、

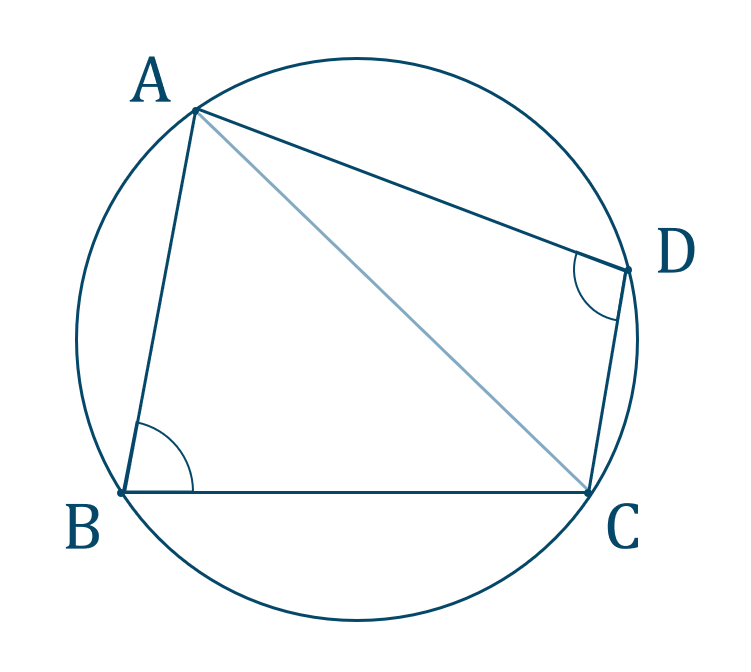
対角の和が $180^\circ$ となることより、$\angle{\rm ABC}=\theta$ とすると、$$~~~\angle {\rm ADC}=180^\circ-\theta$$となります。
これより、$\triangle {\rm ABC}$ について余弦定理を用いると、$$~~~{\rm AC}^2={\rm BA}^2+{\rm BC}^2-2{\rm BA}\cdot{\rm BC}\cos{\theta}~~\cdots{\Large ①}$$
また、$\triangle {\rm ADC}$ について余弦定理を用いると、$$~~~{\rm AC}^2={\rm DA}^2+{\rm DC}^2$$$$\hspace{ 60 pt}-2{\rm DA}\cdot{\rm DC}\cos{(180^\circ-\theta)}$$ここで、補角の公式$$~~~\cos{(180^\circ-\theta)}=-\cos{\theta}$$を用いると、$$~~~{\rm AC}^2={\rm DA}^2+{\rm DC}^2-2{\rm DA}\cdot{\rm DC}(-\cos{\theta})$$$$~~~{\rm AC}^2={\rm DA}^2+{\rm DC}^2+2{\rm DA}\cdot{\rm DC}\cos{\theta}~~\cdots{\Large ②}$$
よって、①と②を連立することより、対角線 ${\rm AC}$ と $\cos{\theta}$ の値を求めることができます。

問題解説：円に内接する四角形

問題解説(1)

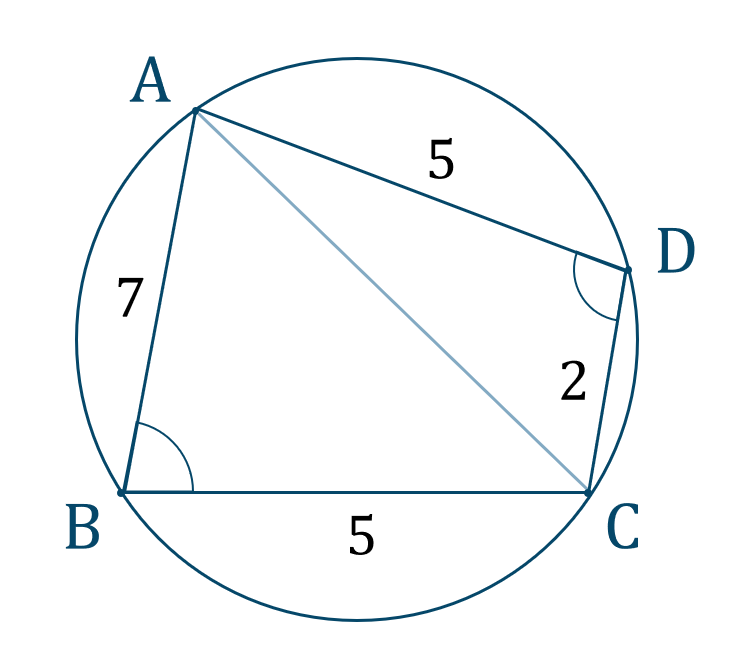
問題円に内接する四角形 ${\rm ABCD}$ についてわ以下の条件のとき、次の問いに答えよ。$$~~~{\rm AB}=7~,~{\rm BC}=5~,~{\rm CD}=2~,~{\rm DA}=5$$${\small (1)}$ $\angle{\rm ABC}$ の値

与えられた図形は次のようになります。

${\rm AC}=x~,~\angle{\rm ABC}=\theta$ とすると、四角形 ${\rm ABCD}$ は円に内接しており、対角の和が $180^\circ$ となることより、$$~~~\angle {\rm ADC}=180^\circ-\theta$$となります。
$\triangle {\rm ABC}$ について、余弦定理を用いると、$$\hspace{ 10 pt}x^2=5^2+7^2-2\cdot5\cdot7\cdot\cos{\theta}$$$$\hspace{ 10 pt}x^2=25+49-70\cos{\theta}$$$$\hspace{ 10 pt}x^2=74-70\cos{\theta}~~\cdots{\Large ①}$$
また、$\triangle {\rm ADC}$ について、余弦定理を用いると、$$\hspace{ 10 pt}x^2=2^2+5^2-2\cdot2\cdot5\cdot\cos{(180^\circ-\theta)}$$ここで、補角の公式$$~~~\cos{(180^\circ-\theta)}=-\cos{\theta}$$を用いると、$$\hspace{ 10 pt}x^2=4+25-20(-\cos{\theta})$$$$\hspace{ 10 pt}x^2=29+20\cos{\theta}~~\cdots{\Large ②}$$

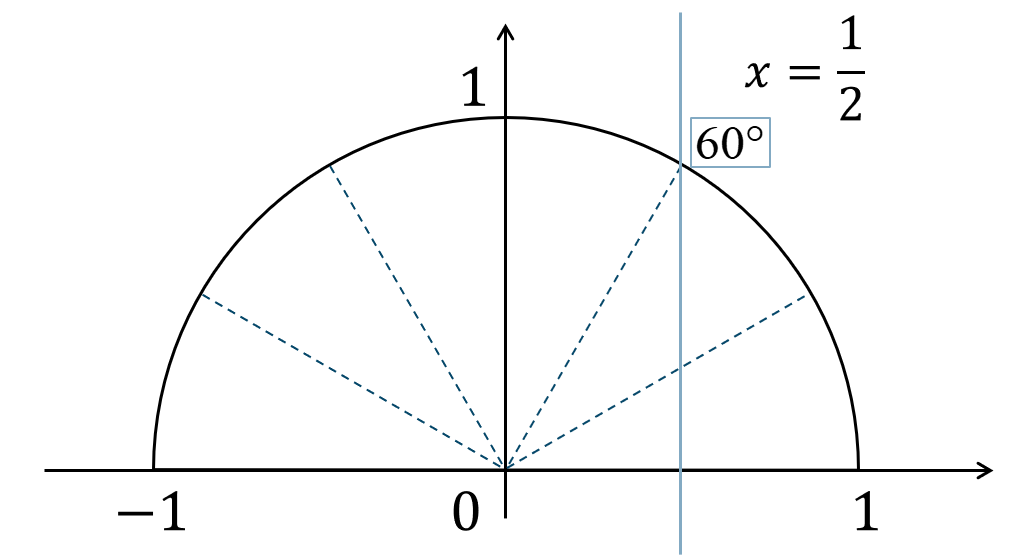
したがって、①と②連立し $x^2$ を消去すると、$$\hspace{ 10 pt}74-70\cos{\theta}=29+20\cos{\theta}$$移項すると、$$\hspace{ 10 pt}-70\cos{\theta}-20\cos{\theta}=29-74$$$$\hspace{ 54 pt}-90\cos{\theta}=-45$$両辺を $-90$ で割ると、$$\hspace{ 10 pt}\cos{\theta}=\frac{-45}{-90}$$$$\hspace{ 10 pt}\cos{\theta}=\frac{1}{2}$$これより、単位円上に表すと、
$$~~~\theta=60^\circ$$よって、答えは$$~~~\angle{\rm ABC}=60^\circ$$となります。

問題解説(2)

問題円に内接する四角形 ${\rm ABCD}$ についてわ以下の条件のとき、次の問いに答えよ。$$~~~{\rm AB}=7~,~{\rm BC}=5~,~{\rm CD}=2~,~{\rm DA}=5$$${\small (2)}$ 対角線 ${\rm AC}$

②の式より、$$\hspace{ 10 pt}x^2=29+20\cos{\theta}$$$\theta=60^\circ$ であるので、$$\hspace{ 10 pt}x^2=29+20\cos{60^\circ}$$$$\hspace{ 10 pt}x^2=29+20\cdot\frac{1}{2}$$$$\hspace{ 10 pt}x^2=29+10$$$$\hspace{ 10 pt}x^2=39$$ここで、$x>0$ であることより、$$\hspace{ 10 pt}x=\sqrt{39}$$よって、答えは$$~~~{\rm AC}=\sqrt{39}$$となります。

問題解説(3)

問題円に内接する四角形 ${\rm ABCD}$ についてわ以下の条件のとき、次の問いに答えよ。$$~~~{\rm AB}=7~,~{\rm BC}=5~,~{\rm CD}=2~,~{\rm DA}=5$$${\small (3)}$ 四角形 ${\rm ABCD}$ の面積

与えられた図形に値を書き入れると、

円に内接する四角形より、内角の和が $180^\circ$ となるので、$$\hspace{ 10 pt}\angle{\rm ADC}=180^\circ-\angle{\rm ABC}$$$$\hspace{ 43 pt}=180^\circ-60^\circ$$$$\hspace{ 43 pt}=120^\circ$$となります。
$\triangle {\rm ABC}$ の面積を $S_1$ とすると、$$\hspace{ 10 pt}S_1=\frac{1}{2}\cdot7\cdot5\cdot\sin{60^\circ}$$$$\hspace{ 23 pt}=\frac{35}{2}\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 23 pt}=\frac{35\sqrt{3}}{4}$$
また、$\triangle {\rm ADC}$ の面積を $S_2$ とすると、$$\hspace{ 10 pt}S_2=\frac{1}{2}\cdot5\cdot2\cdot\sin{120^\circ}$$$$\hspace{ 23 pt}=5\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 23 pt}=\frac{5\sqrt{3}}{2}$$
したがって、四角形 ${\rm ABCD}$ の面積は$$~~~~~~S_1+S_2$$$$~=\frac{35\sqrt{3}}{4}+\frac{5\sqrt{3}}{2}$$$$~=\frac{35\sqrt{3}+10\sqrt{3}}{4}$$$$~=\frac{45\sqrt{3}}{4}$$よって、答えは$$~~~\frac{45\sqrt{3}}{4}$$となります。