2次不等式の解(交点がない)
② 左辺が因数分解できない場合
左辺=0の2次方程式の解の判別式 \(D\) を考えます。
\(D>0\) となるとき、左辺を \(y\) としたグラフは \(x\) 軸と交わりません。
③ グラフを描き、2次不等式の解を求めます。
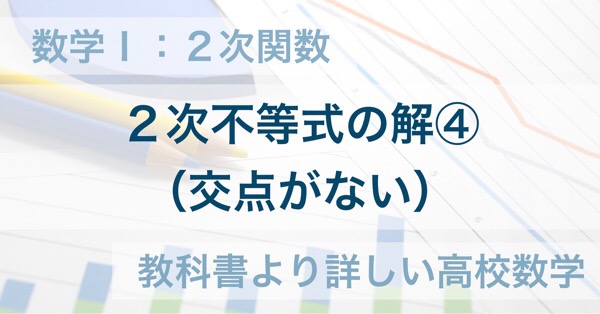
(1) \(ax^2+bx+c≧0\) のとき
グラフが範囲内にすべて含まれるので、答えは
となります。
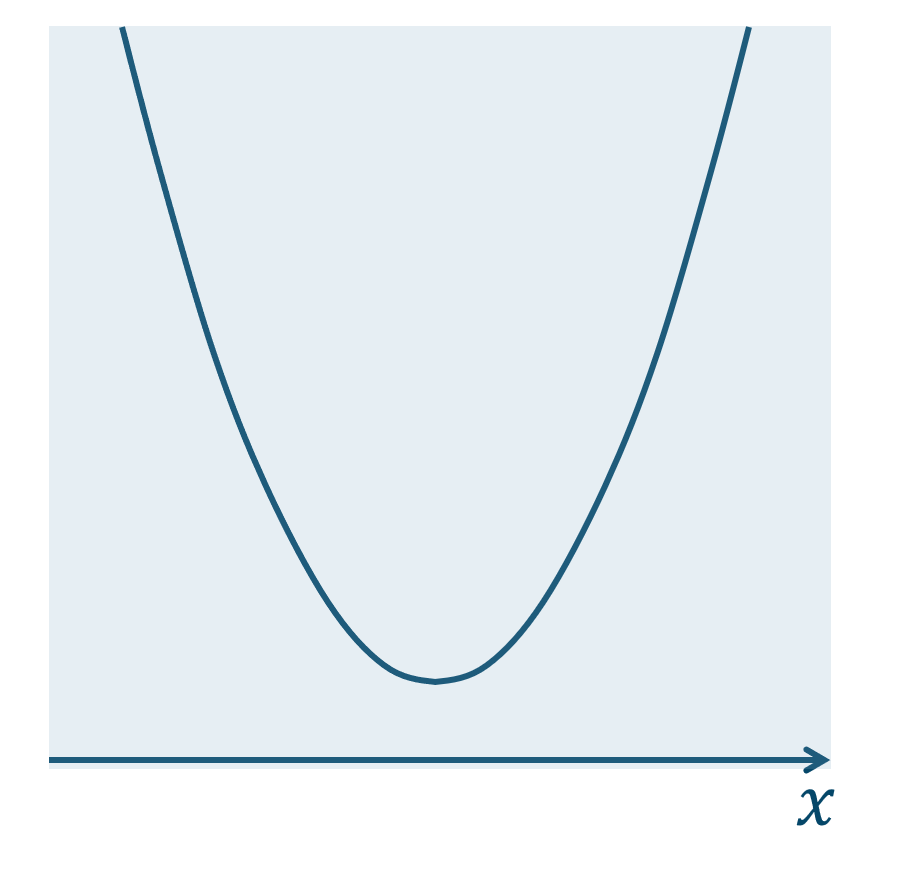
(2) \(ax^2+bx+c>0\) のとき
グラフが範囲内にすべて含まれるので、答えは
となります。
(3) \(ax^2+bx+c≦0\) のとき

グラフが範囲内にないので、答えは
となります。
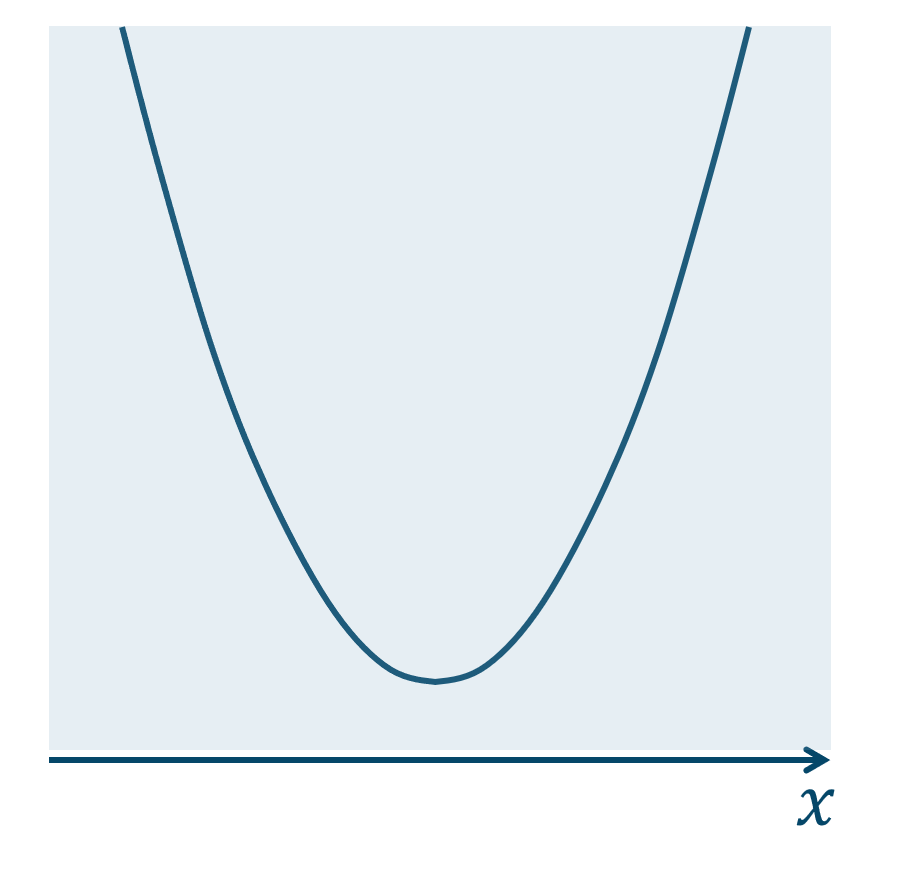
(4) \(ax^2+bx+c<0\) のとき
グラフが範囲内にないので、答えは
となります。
問題解説:2次不等式の解④(交点がない)
問題解説(1)
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=4^2-4\cdot1\cdot9$$$$\hspace{ 20 pt}=16-36$$$$\hspace{ 20 pt}=-20<0$$よって、\(x\) 軸と交わらないので、左辺を \(y\) としたグラフは次のようになります。

このグラフより \(y≧0\) となるような範囲が解となり、グラフのすべてが範囲内にあるので、
答えは、「すべての実数」となります。
問題解説(2)
\(x^2\) の係数が負の数であるので、両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$~~~x^2-4x+9<0$$となります。
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=4^2-4\cdot1\cdot9$$$$\hspace{ 20 pt}=16-36$$$$\hspace{ 20 pt}=-20<0$$よって、\(x\) 軸と交わらないので、左辺を \(y\) としたグラフは次のようになります。

このグラフより \(y<0\) となるような範囲が解となりますが、範囲内にグラフがないので、
答えは、「解なし」となります。
問題解説(3)
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=4^2-4\cdot1\cdot9$$$$\hspace{ 20 pt}=16-36$$$$\hspace{ 20 pt}=-20<0$$よって、\(x\) 軸と交わらないので、左辺を \(y\) としたグラフは次のようになります。

このグラフより \(y≦0\) となるような範囲が解となりますが、範囲内にグラフがないので、
答えは、「解なし」となります。
問題解説(4)
\(x^2\) の係数が負の数であるので、両辺に \(-1\) をかけると、不等号の向きが逆になるので、$$~~~x^2-4x+9>0$$となります。
左辺が因数分解できないので、(左辺)=0の2次方程式の判別式 \(D\) を考えると、$$\hspace{ 10 pt}D=4^2-4\cdot1\cdot9$$$$\hspace{ 20 pt}=16-36$$$$\hspace{ 20 pt}=-20<0$$よって、\(x\) 軸と交わらないので、左辺を \(y\) としたグラフは次のようになります。

このグラフより \(y>0\) となるような範囲が解となり、グラフのすべてが範囲内にあるので、
答えは、「すべての実数」となります。
今回のまとめ
全4回で2次不等式の解について解説していきました。因数分解できるパターンでもできないパターンでも、最終的にグラフを描いて視覚的に解くことを覚えておきましょう。