【教科書レベルの問題一覧と解答】数学Ⅲ｜複素数平面

このページは「高校数学Ⅲ：複素数平面」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。

【問題一覧】数学Ⅲ：複素数平面

複素数平面上の点

問題次の問いに答えよ。
${\small (1)}~$下の図において、点Ａ〜Ｅはそれぞれどのような複素数を表すか答えよ。

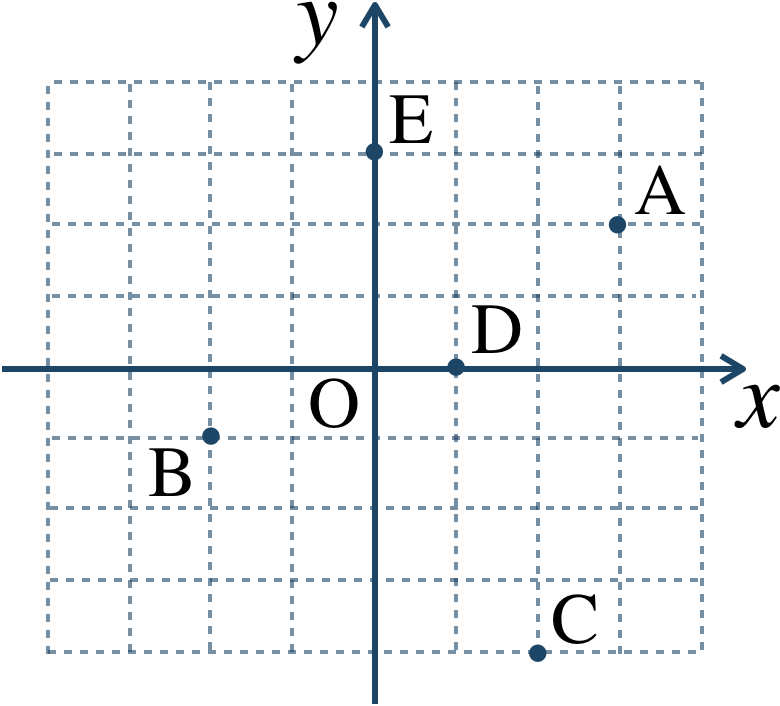
${\small (2)}~$次の点を複素数平面上に表せ。$$~{\large ①}~{\rm F}(-3+i)~~~~{\large ②}~{\rm G}(4-i)$$$$~{\large ③}~{\rm H}(-1)~~~~~~~~~{\large ④}~{\rm I}(-3i)$$

[ 解答を見る ]

【解答】
${\small (1)}~$${\rm A}(3+2i)~,~{\rm B}(-2-i)$
$~~~~{\rm C}(2-4i)~,~{\rm D}(1)~,~{\rm E}(3i)$
${\small (2)}~$略

詳しい解説ページはこちらから↓

複素数平面上の点

今回は複素数平面上の点について解説していきます。複素数を座標平面上に表す方法を覚えていきましょう。

複素数平面上の複素数の和・差

問題次の図の複素数平面上の２点 ${\rm A}(\alpha)~,~{\rm B}(\beta)$ について、次の複素数を求め図示せよ。

$${\small (1)}~\alpha+\beta~~~~~{\small (2)}~\alpha-\beta$$$${\small (3)}~\beta-\alpha~~~~~{\small (4)}~\alpha+2\beta$$

[ 解答を見る ]

【解答】$${\small (1)}~5+2i$$$${\small (2)}~-1+4i$$$${\small (3)}~1-4i$$$${\small (4)}~8+i$$図は省略

詳しい解説ページはこちらから↓

複素数平面上の複素数の和・差

今回は複素数平面上の複素数の和・差の求め方について解説していきます。計算だけでなく、図形的な意味も理解しておきましょう。

複素数平面上の対称移動

問題複素数 $z=3+2i$ を次のものに関して対称移動した点を複素数で表せ。また、その複素数を $z$ を用いて表せ。
${\small (1)}~$実軸に関して対称な点
${\small (2)}~$虚軸に関して対称な点
${\small (3)}~$原点に関して対称な点

[ 解答を見る ]

【解答】$${\small (1)}~3-2i~,~\overline {z}$$$${\small (2)}~-3+2i~,~-\overline {z}$$$${\small (3)}~-3-2i~,~-z$$

詳しい解説ページはこちらから↓

複素数平面上の対称移動

今回は複素数平面上の点の対称移動について解説していきます。共役な複素数を用いて表す方法もおさえておきましょう。

複素数の絶対値

問題次の問いに答えよ。
${\small (1)}~$次の複素数の絶対値を求めよ。$$~{\large ①}~1+2i~~~~~~~~{\large ②}~3-4i$$$$~{\large ③}~-3i~~~~~~~~~~{\large ④}~5$$${\small (2)}~$複素数 $z$ について、次のことを証明せよ。$$~{\large ①}~|z|=|-z|=|\overline {z}|$$$$~{\large ②}~|z|^2=z\overline {z}$$

[ 解答を見る ]

【解答】$${\small (1)}~{\large ①}~\sqrt{5}~~~~~{\large ②}~5$$$$~~~~~{\large ③}~3~~~~~~~{\large ④}~5$$${\small (2)}~$略

詳しい解説ページはこちらから↓

複素数の絶対値

今回は複素数の絶対値について解説していきます。絶対値の求め方と性質を覚えていきましょう。

複素数平面上の２点間の距離

問題次の２点間の距離を求めよ。$${\small (1)}~\alpha=-1+2i~,~\beta=3+5i$$$${\small (2)}~\alpha=-5-6i~,~\beta=1-2i$$

[ 解答を見る ]

【解答】$${\small (1)}~5~~~~~{\small (2)}~2\sqrt{13}$$

詳しい解説ページはこちらから↓

複素数平面上の２点間の距離

今回は複素数平面上の２点間の距離について解説していきます。複素数の差を求めて、絶対値を求める手順を覚えていきましょう。

複素数の極形式

問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (1)}~1+i~~~~~~~~~{\small (2)}~-1+i$$$${\small (3)}~\sqrt{3}-i~~~~~~{\small (4)}~-3-\sqrt{3}i$$$${\small (5)}~-3~~~~~~~~~~{\small (6)}~-3i$$

[ 解答を見る ]

【解答】$${\small (1)}~\sqrt{2}\left(\cos{\frac{\,\pi\,}{\,4\,}}+i\sin{\frac{\,\pi\,}{\,4\,}}\right)$$$${\small (2)}~\sqrt{2}\left(\cos{\frac{\,3\,}{\,4\,}\pi}+i\sin{\frac{\,3\,}{\,4\,}\pi}\right)$$$${\small (3)}~2\left(\cos{\frac{\,11\,}{\,6\,}\pi}+i\sin{\frac{\,11\,}{\,6\,}\pi}\right)$$$${\small (4)}~2\sqrt{3}\left(\cos{\frac{\,7\,}{\,6\,}\pi}+i\sin{\frac{\,7\,}{\,6\,}\pi}\right)$$$${\small (5)}~3\left(\cos{\pi}+i\sin{\pi}\right)$$$${\small (6)}~3\left(\cos{\frac{\,3\,}{\,2\,}\pi}+i\sin{\frac{\,3\,}{\,2\,}\pi}\right)$$

詳しい解説ページはこちらから↓

複素数の極形式

今回は複素数の極形式を求める方法を解説していきます。複素数の絶対値と偏角を求めて、極形式を導けるようにしましょう。

極形式の積と商

問題$\alpha=-1+\sqrt{3}i~,~\beta=2-2i$ のとき、次の式を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt2\pi$ とする。$${\small (1)}~\alpha\beta~~~~~~~~~~~~{\small (2)}~\frac{\,\alpha\,}{\,\beta\,}$$

[ 解答を見る ]

【解答】$${\small (1)}~4\sqrt{2}\left(\cos{\frac{\,5 \,}{\,12 \,}\pi}+i\sin{\frac{\,5 \,}{\,12 \,}\pi}\right)$$$${\small (2)}~\frac{\,\sqrt{2} \,}{\,2 \,}\left(\cos{\frac{\,11 \,}{\,12 \,}\pi}+i\sin{\frac{\,11 \,}{\,12 \,}\pi}\right)$$

詳しい解説ページはこちらから↓

極形式の積と商

今回は極形式の積と商を求める方法を解説していきます。それぞれの絶対値と偏角をどのように計算するかを覚えていきましょう。

複素数の回転移動

問題次の問いに答えよ。
${\small (1)}~$$z=1+\sqrt{3}i$ とするとき、点 $z$ を原点を中心に次の角だけ回転した点の複素数を求めよ。$$~{\large ①}~\frac{\, \pi\,}{\,3 \,}~~~~~~~~~~{\large ②}~-\frac{\,\pi \,}{\,6 \,}$$${\small (2)}~$次の複素数は点 $z$ をどのように移動した点か答えよ。$$~{\large ①}~(1+i)z~~~~~~~~~~{\large ②}~(\sqrt{3}-i)z$$

[ 解答を見る ]

【解答】
$${\small (1)}~{\large ①}~-1+\sqrt{3}i~~~~~{\large ②}~\sqrt{3}+i$$${\small (2)}$
$~~~{\large ①}~$点 $z$ を原点を中心に ${\large \frac{\,\pi\,}{\,4\,}}$ だけ回転して、原点からの距離を $\sqrt{2}$ 倍した点
$~~~{\large ②}~$点 $z$ を原点を中心に $-{\large \frac{\,\pi\,}{\,6\,}}$ だけ回転して、原点からの距離を $2$ 倍した点

詳しい解説ページはこちらから↓

複素数の回転移動

今回は複素数の回転移動を求める方法を解説していきます。複素数をかけ算すると、どのように回転移動するかをおさえておきましょう。

点を中心とする回転

問題複素数平面上の点について、次の問いに答えよ。
${\small (1)}~$点 ${\rm A}(1+i)$ を中心として、点 ${\rm B}(3+2i)$ を ${\large \frac{\,\pi\,}{\,6\,}}$ 回転させた点 ${\rm C}$ を複素数で表せ。
${\small (2)}~$点 ${\rm A}(1+2i)$ を中心として、点 ${\rm B}(5+4i)$ を ${\large \frac{\,\pi\,}{\,2\,}}$ 回転させた点 ${\rm C}$ を複素数で表せ。

[ 解答を見る ]

【解答】$${\small (1)}~\frac{\,2\sqrt{3}+1 \,}{\,2 \,}+\frac{\, \sqrt{3}+4\,}{\,2 \,}i$$$${\small (2)}~-1+6i$$

詳しい解説ページはこちらから↓

点を中心とする回転

今回は原点以外の点を中心とする回転移動を求める方法を解説していきます。原点に平行移動させる方法を覚えていきましょう。

三角形の頂点と点の回転

問題複素数平面上の点について、次の問いに答えよ。
${\small (1)}~$３点 ${\rm A}(2+i)~,~{\rm B}(4+5i)~,~{\rm C}$ について、$\triangle {\rm ABC}$ が正三角形となるとき、点 ${\rm C}$ を表す複素数を求めよ。
${\small (2)}~$３点 ${\rm O}(0)~,~{\rm A}(2+i)~,~{\rm B}$ について、$\triangle {\rm OAB}$ が $\angle {\rm AOB}$ が直角である直角二等辺三角形となるとき、点 ${\rm B}$ を表す複素数を求めよ。

[ 解答を見る ]

【解答】
$${\small (1)}~\left(3-2\sqrt{3}\right)+\left(3+\sqrt{3}\right)i$$$$~~~~,~\left(3+2\sqrt{3}\right)+\left(3-\sqrt{3}\right)i$$まとめて、$$~~~\left(3\pm2\sqrt{3}\right)+\left(3\mp\sqrt{3}\right)i$$ただし、符号同順
$${\small (2)}~-1+2i~,~1-2i$$まとめて、$$~~~\pm1\mp2i$$ただし、符号同順

詳しい解説ページはこちらから↓

三角形の頂点と点の回転

今回は複素数平面上の三角形の頂点を求める方法を解説していきます。三角形の条件より、点をどのように回転させればよいかを読み取りましょう。

ド・モアブルの定理

問題次の計算をせよ。$${\small (1)}~\left(\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i\right)^6$$$${\small (2)}~\left(\sqrt{3}-i\right)^9$$$${\small (3)}~(-1+i)^{-4}$$

[ 解答を見る ]

【解答】$${\small (1)}~1~~~~~{\small (2)}~512i~~~~~{\small (3)}~-\frac{\,1 \,}{\,4 \,}$$

詳しい解説ページはこちらから↓

ド・モアブルの定理

今回は複素数のド・モアブルの定理について解説していきます。絶対値と偏角のそれぞれの計算方法をおさえておきましょう。

１のn乗根

問題次の問いに答えよ。
${\small (1)}~$１の $4$ 乗根を方程式 $z^4=1$ より求めよ。
${\small (2)}~$１の $6$ 乗根を方程式 $z^6=1$ より求めよ。

[ 解答を見る ]

【解答】
$${\small (1)}~z=1~,~-1~,~i~,~-i$$まとめて、$$~~~~z=\pm1~,~\pm i$$
$${\small (2)}~z=1~,~-1$$$$~~~~~~~~,~\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i~,~-\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i$$$$~~~~~~~~,~\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i~,~-\frac{\,1 \,}{\,2 \,}-\frac{\,\sqrt{3} \,}{\,2 \,}i$$まとめて、$$~~~z=\pm1~,~\pm \frac{\,1 \,}{\,2 \,}\pm\frac{\,\sqrt{3} \,}{\,2 \,}i$$

詳しい解説ページはこちらから↓

１のn乗根

今回は１のn乗根の求め方について解説していきます。ド・モアブルの定理を用いて方程式を解く方法を覚えていきましょう。

複素数を含む方程式の解

問題次の方程式の解を求めよ。$${\small (1)}~z^4=9$$$${\small (2)}~z^4=-2+2\sqrt{3}i$$$${\small (3)}~z^3=-8i$$

[ 解答を見る ]

【解答】
$${\small (1)}~z=\sqrt{3}~,~-\sqrt{3}~,~\sqrt{3}i~,~-\sqrt{3}i$$まとめて、$$~~~z=\pm\sqrt{3}~,~\pm \sqrt{3}i$$$${\small (2)}~z=\frac{\,\sqrt{6} \,}{\,2 \,}+\frac{\,\sqrt{2} \,}{\, 2\,}i~,~-\frac{\,\sqrt{2} \,}{\,2 \,}+\frac{\,\sqrt{6} \,}{\, 2\,}i$$$$~~~~~~~,~-\frac{\,\sqrt{6} \,}{\,2 \,}-\frac{\,\sqrt{2} \,}{\, 2\,}i~,~\frac{\,\sqrt{2} \,}{\,2 \,}-\frac{\,\sqrt{6} \,}{\, 2\,}i$$まとめて、$$~~~z=\pm\frac{\,\sqrt{6} \,}{\,2 \,}\pm\frac{\,\sqrt{2} \,}{\, 2\,}i~,~\mp\frac{\,\sqrt{2} \,}{\,2 \,}\pm\frac{\,\sqrt{6} \,}{\, 2\,}i$$ただし、符号同順$${\small (3)}~z=2i~,~-\sqrt{3}-i~,~\sqrt{3}-i$$まとめて、$$~~~z=2i~,~\pm\sqrt{3}-i$$

詳しい解説ページはこちらから↓

複素数を含む方程式の解

今回は複素数を含む方程式の解の求め方について解説していきます。１のn乗根の求め方と同様に解法の手順をおさえておきましょう。

複素数平面上の内分点・外分点・重心

問題複素数平面上の３点 ${\rm A}(4+i)$ 、${\rm B}(2+3i)$ 、${\rm C}(-1+2i)$ について、次の点を表す複素数を求めよ。
${\small (1)}~$線分 ${\rm AB}$ の中点 ${\rm M}$
${\small (2)}~$線分 ${\rm BC}$ を $1\,:\,2$ に内分する点 ${\rm P}$
${\small (3)}~$線分 ${\rm AC}$ を $3\,:\,2$ に外分する点 ${\rm Q}$
${\small (4)}~$$\triangle {\rm ABC}$ の重心 ${\rm G}$

[ 解答を見る ]

【解答】$${\small (1)}~{\rm M}(3+2i)$$$${\small (2)}~{\rm P}\left(1+{ \frac{\,8\,}{\,3\,}}i\right)$$$${\small (3)}~{\rm Q}(-11+4i)$$$${\small (4)}~{\rm G}\left({ \frac{\,5\,}{\,3\,}}+2i\right)$$

詳しい解説ページはこちらから↓

複素数平面上の内分点・外分点・重心

今回は複素数平面上の内分点・外分点・重心の求め方について解説していきます。複素数を含むそれぞれの公式をおさえておきましょう。

複素数の表す図形

問題次の方程式を満たす点 $z$ の全体はどのような図形を表すか答えよ。$${\small (1)}~|z-2|=|z-1+2i|$$$${\small (2)}~|2z-1|=|2z-i|$$$${\small (3)}~|z-2+3i|=3$$$${\small (4)}~\left(2z+3i\right)\left(2\overline {z}-3i\right)=16$$

[ 解答を見る ]

【解答】
${\small (1)}~$２点 ${\rm A}(2)$ 、${\rm B}(1-2i)$ を結ぶ線分 ${\rm AB}$ の垂直二等分線
${\small (2)}~$２点 ${\rm A}\left({\large \frac{\,1\,}{\,2\,}}\right)$ 、${\rm B}\left({\large \frac{\,1\,}{\,2\,}}i\right)$ を結ぶ線分 ${\rm AB}$ の垂直二等分線
${\small (3)}~$点 ${\rm A}(2-3i)$ を中心とする半径 $3$ の円
${\small (4)}~$点 ${\rm A}\left(-{\large \frac{3}{2}}i\right)$ を中心とする半径 $2$ の円

詳しい解説ページはこちらから↓

複素数の表す図形

今回は複素数の表す図形の求め方について解説していきます。垂直二等分線と円を表す複素数の方程式の形をおさえておきましょう。

単位円上の点と複素数の表す図形

問題点 $z$ が単位円上を動くとき、次の方程式を満たす点 $w$ はどのような図形か答えよ。$${\small (1)}~w=z+i$$$${\small (2)}~w=i(3z-2)$$

[ 解答を見る ]

【解答】
${\small (1)}~$点 ${\rm A}(i)$ を中心とする半径 $1$ の円
${\small (2)}~$点 ${\rm A}(-2i)$ を中心とする半径 $3$ の円

詳しい解説ページはこちらから↓

単位円上の点と複素数の表す図形

今回は単位円上の点と複素数の表す図形の求め方について解説していきます。式変形の方法と単位円上にある条件を利用しましょう。

アポロニウスの円

問題複素数平面上の点について、次の問いに答えよ。
${\small (1)}~$次の方程式を表す点 $z$ 全体はどのような図形か答えよ。$$~~~2|z-1|=|z+2|$$${\small (2)}~$２点 ${\rm A}(2i)~,~{\rm B}(-2i)$ からの距離の比が $1\,:\,3$ である点 ${\rm P}(z)$ 全体はどのような図形か答えよ。

[ 解答を見る ]

【解答】
${\small (1)}~$点 $(2)$ を中心とする半径 $2$ の円
${\small (2)}~$点 $\left({\large \frac{\,5\,}{\,2\,}}i\right)$ を中心とする半径 ${\large \frac{\,3\,}{\,2\,}}$ の円

詳しい解説ページはこちらから↓

アポロニウスの円

今回は複素数平面上のアポロニウスの円の求め方について解説していきます。式変形が少し特殊ですので、解法の手順をしっかりとおさえておきましょう。

複素数平面上の直線のなす角

問題複素数平面上の点について、次の問いに答えよ。
${\small (1)}~$２点 ${\rm A}\left(1-\sqrt{3}i\right)~,~{\rm B}\left(4+2\sqrt{3}i\right)$ において、直線 ${\rm AB}$ と実軸との正の向きとのなす角を求めよ。
${\small (2)}~$３点 ${\rm A}(-3+2i)~,~{\rm B}(2i)~,~{\rm C}(-9+8i)$ において、$\angle{\rm BAC}$ を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~{ \frac{\,\pi\,}{\,3\,}}~~~~~~{\small (2)}~{ \frac{\,3\,}{\,4\,}}\pi$$

詳しい解説ページはこちらから↓

複素数平面上の直線のなす角

今回は複素数平面上の直線のなす角の求め方について解説していきます。条件より複素数を求めて、その偏角がなす角となることを覚えていきましょう。

複素数平面上の一直線・垂直条件

問題複素数平面上の３点 ${\rm A}(-2+3i)$$~,~$${\rm B}(i)$$~,~$${\rm C}(2+ai)$ について、次の問いに答えよ。ただし、$a$ は実数の定数とする。
${\small (1)}~$３点 ${\rm A~,~B~,~C}$ が一直線上にあるとき、定数 $a$ の値を求めよ。
${\small (2)}~$２直線 ${\rm AB~,~AC}$ が垂直であるとき、定数 $a$ の値を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~a=-1~~~~~{\small (2)}~a=7$$

詳しい解説ページはこちらから↓

複素数平面上の一直線・垂直条件

今回は複素数平面上の一直線・垂直条件について解説していきます。３点が一直線上にある条件と２直線が垂直である条件を、それぞれおさえておきましょう。

複素数平面上の三角形の形状

問題複素数平面上の３点 ${\rm A}(\alpha)$$~,~$${\rm B}(\beta)$$~,~$${\rm C}(\gamma)$ について、次の条件を満たす $\triangle {\rm ABC}$ はどのような三角形となるか答えよ。$${\small (1)}~\beta-\alpha=(\gamma-\alpha)i$$$${\small (2)}~\alpha-\beta=\left(1+\sqrt{3}i\right)(\gamma-\beta)$$

[ 解答を見る ]

【解答】
${\small (1)}~$$\angle{\rm CAB}={\large \frac{\,\pi\,}{\,2\,}}$ 、${\rm AB=AC}$ の直角二等辺三角形
${\small (2)}~$$$~~~{\rm BC\,:\,BA\,:\,AC}=1\,:\,2\,:\,\sqrt{3}$$$$~~~\angle{\rm A}=\frac{\,\pi \,}{\,6 \,}~,~\angle{\rm B}=\frac{\,\pi \,}{\,3 \,}~,~\angle{\rm C}=\frac{\,\pi \,}{\,2 \,}$$　の直角三角形

詳しい解説ページはこちらから↓