このページは「高校数学Ⅰ:2次関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします!
- 【問題一覧】数学Ⅰ:2次関数
- 関数の値と象限
- 関数の値域と最大値・最小値
- 2次関数のグラフ
- 2次関数の平方完成
- 2次関数のグラフの平行移動
- 平行移動後のグラフ
- グラフの対称移動
- 2次関数の決定①(頂点)
- 2次関数の決定②(3点を通る)
- 2次関数の最大値・最小値
- 2次関数の決定③(最大値・最小値)
- 最大値・最小値の文章問題
- 文字係数を含む2次関数の最大値・最小値
- 定義域が変化する2次関数の最大値・最小値
- 2次方程式の解
- 2次方程式の解の個数
- 2次方程式の解の条件
- 解が与えられた2次方程式
- 2次方程式の文章問題
- 2次関数とx軸との交点
- 2次関数とx軸との交点の条件
- 放物線と直線の交点
- 2次不等式の解①(因数分解)
- 2次不等式の解②(x軸と接する)
- 2次不等式の解③(解の公式)
- 2次不等式の解④(交点がない)
- 連立2次不等式の解
- 絶対不等式
- 2次不等式の文章問題
- 2次方程式の解の符号(2次関数)
【問題一覧】数学Ⅰ:2次関数
関数の値と象限
\({\small (1)}~\)関数 \(f(x)=2x-3\) について、次の関数の値を求めよ。$$~~~{\large ①}~f(2)~~~~~~{\large ②}~f(3a)~~~~~~{\large ③}~f(a-1)$$\({\small (2)}~\)次の点は第何象限の点か答えよ。$$~~~{\large ①}~(-2,-3)~~~~{\large ②}~(-5,1)~~~~{\large ③}~(1,-4)$$
[ 解答を見る ]
【解答】$${\small (1)}~{\large ①}~f(2)=1~~~~~~{\large ②}~f(3a)=6a-3$$$$~~~~~{\large ③}~f(a-1)=2a-5$$\({\small (2)}~\)\({\large ①}~\)第3象限 \({\large ②}~\)第2象限
\(~{\large ③}~\)第4象限
詳しい解説ページはこちらから↓

関数の値域と最大値・最小値
[ 解答を見る ]
【解答】
\({\small (1)}~\)値域は \(-1≦y\)
最大値はなし、
\(x=1\) のとき、最小値は \(-1\)
\({\small (2)}~\)値域は \(-7≦y≦5\)
\(x=-1\) のとき、最大値は \(5\)
\(x=5\) のとき、最小値は \(-7\)
\({\small (3)}~\)値域は \(-5≦y≦7\)
\(x=5\) のとき、最大値は \(7\)
\(x=-1\) のとき、最小値は \(-5\)
\({\small (4)}~\)値域は \(-1<y≦9\)
\(x=-3\) のとき、最大値は \(9\)
最小値はなし
詳しい解説ページはこちらから↓

2次関数のグラフ
[ 解答を見る ]
【解答】
\({\small (1)}~\)
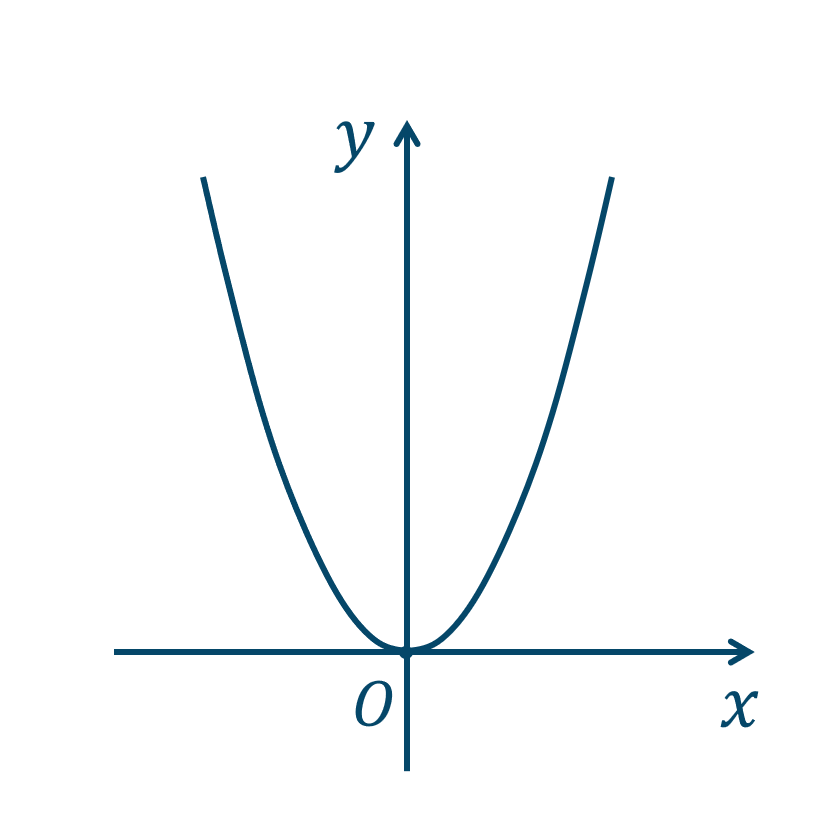
\({\small (2)}~\)
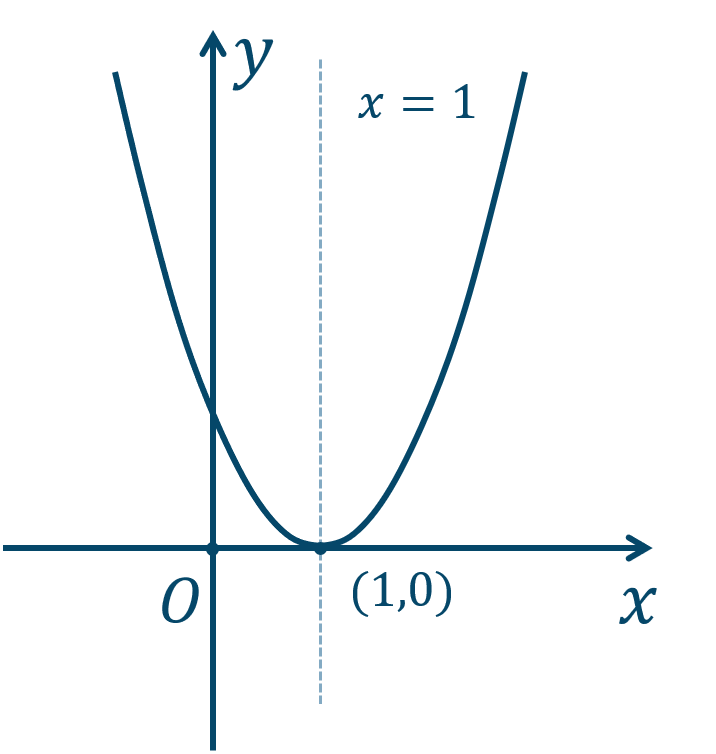
\({\small (3)}~\)

\({\small (4)}~\)

詳しい解説ページはこちらから↓


2次関数の平方完成
[ 解答を見る ]
【解答】
\({\small (1)}~\)頂点と軸は、$$~~~(2,-1)~~,~~x=2$$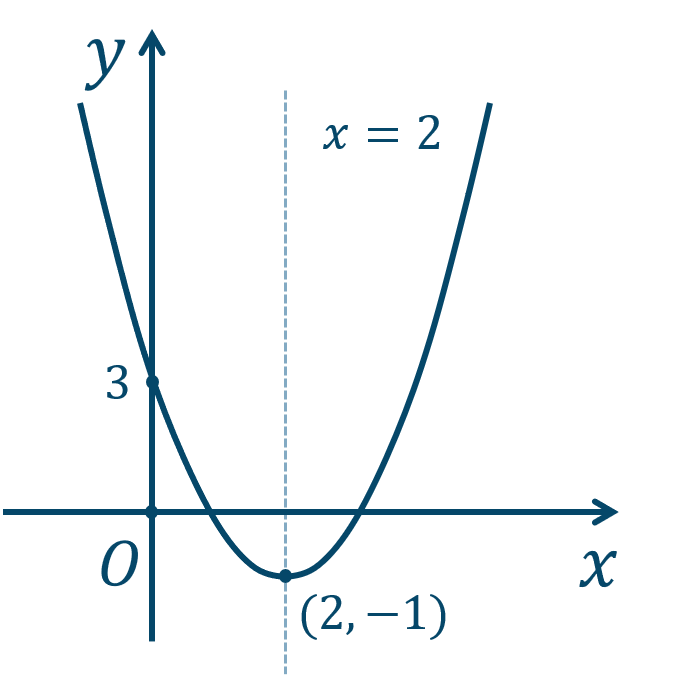
\({\small (2)}~\)頂点と軸は、$$~~~(-3,-5)~~,~~x=-3$$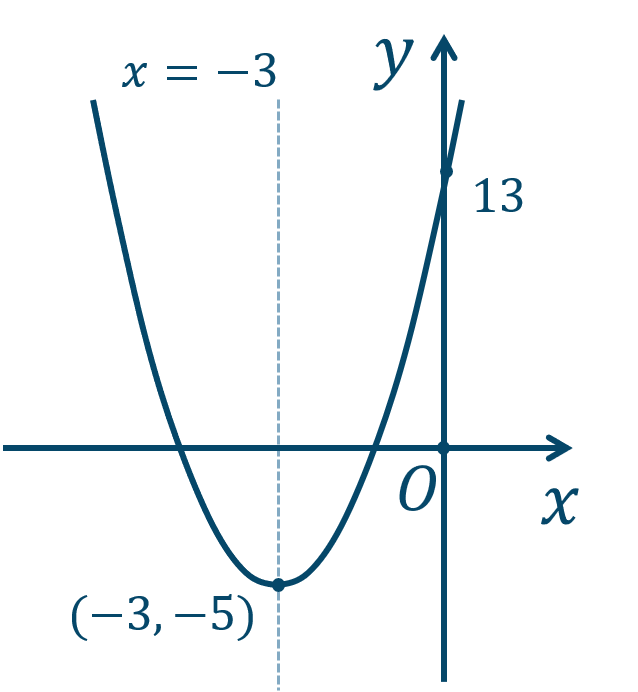
\({\small (3)}~\)頂点と軸は、$$~~~\left( \frac{1}{3},\frac{4}{3} \right)~~,~~x=\frac{1}{3}$$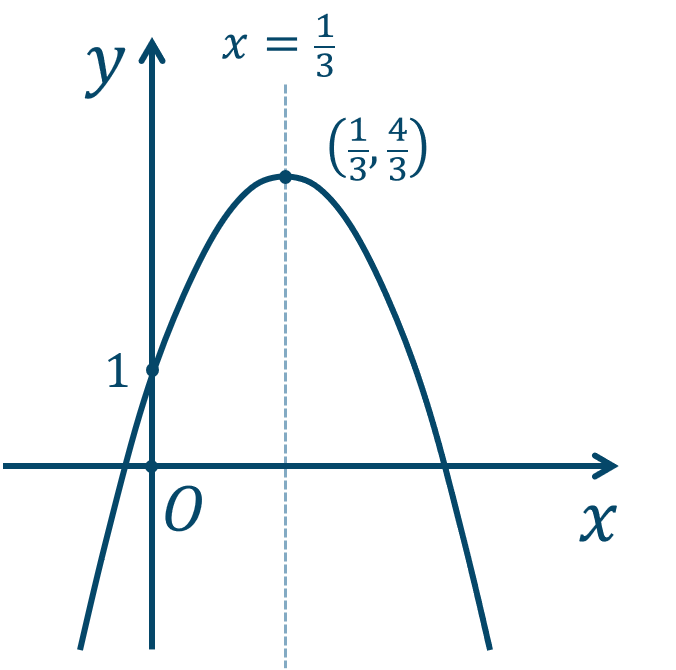
詳しい解説ページはこちらから↓


2次関数のグラフの平行移動
[ 解答を見る ]
【解答】
\(x\) 軸方向に \(-2\)、\(y\) 軸方向に \(10\) だけ平行移動
詳しい解説ページはこちらから↓


平行移動後のグラフ
[ 解答を見る ]
【解答】$$~~~~y=2x^2-9x+5$$
詳しい解説ページはこちらから↓


グラフの対称移動
\({\small (1)}~\)\(x\) 軸に対して対称移動
\({\small (2)}~\)\(y\) 軸に対して対称移動
\({\small (3)}~\)原点に対して対称移動
[ 解答を見る ]
【解答】$${\small (1)}~y=-2x^2+5x-1$$$${\small (2)}~y=2x^2+5x+1$$$${\small (3)}~y=-2x^2-5x-1$$
詳しい解説ページはこちらから↓


2次関数の決定①(頂点)
\({\small (1)}~\)頂点が \((2,3)\) で、点 \((1,5)\) を通る。
\({\small (2)}~\)軸が \(x=1\) で、2点 \((2,4)~,~(-1,1)\) を通る。
[ 解答を見る ]
【解答】$${\small (1)}~y=2(x-2)^2+3$$$${\small (2)}~y=-(x-1)^2+5$$
詳しい解説ページはこちらから↓


2次関数の決定②(3点を通る)
[ 解答を見る ]
【解答】$$~~~~y=-x^2+3x+1$$
詳しい解説ページはこちらから↓

2次関数の最大値・最小値
[ 解答を見る ]
【解答】
\({\small (1)}\) 最大値なし
最小値は、$$~~~-\frac{25}{4}~~~\left(x=-\frac{5}{2}\right)$$\({\small (2)}\) 最大値が$$~~~9~~~(x=3)$$最小値が$$~~~5~~~(x=1)$$\({\small (3)}\) 最大値が$$~~~5~~~(x=3)$$最小値が$$~~~-11~~~(x=-1)$$
詳しい解説ページはこちらから↓


2次関数の決定③(最大値・最小値)
\({\small (1)}\) 次の2次関数の最大値が \(5\) のとき、\(k\) の値を求めよ。$$~~~y=-x^2+4x+k$$\({\small (2)}\) 次の2次関数の最大値が \(3\) のとき、\(k\) の値とこの関数の最小値を求めよ。$$~~~y=x^2+2x+k~~~(-2≦x≦2)$$
[ 解答を見る ]
【解答】$${\small (1)}~k=1$$$${\small (2)}~k=-5$$最小値は、$$~~~-6~~~(x=-1)$$
詳しい解説ページはこちらから↓


最大値・最小値の文章問題
\({\small (1)}\) この針金で長方形を作り面積を最大にするとき、その面積の最大値を求めよ。
\({\small (2)}\) この針金を2つに分けて、2つの正方形を作る。このとき、2つの正方形の面積の和を最小にするにはどのように針金を分ければよいか答えよ。
[ 解答を見る ]
【解答】
\({\small (1)}\) 面積の最大値 \(9\)
\({\small (2)}\) 針金を \(6\) cmずつに分ければよい
詳しい解説ページはこちらから↓


文字係数を含む2次関数の最大値・最小値
[ 解答を見る ]
【解答】
最大値が
( ⅰ ) \(a<2\) のとき$$~~~21-8a~~~(x=4)$$( ⅱ ) \(a=2\) のとき$$~~~5~~~(x=0~,~4)$$( ⅲ ) \(a>2\) のとき$$~~~5~~~(x=0)$$最小値が
( ⅰ ) \(a<0\) のとき$$~~~5~~~(x=0)$$( ⅱ ) \(0≦a≦4\) のとき$$~~~-a^2+5~~~(x=a)$$( ⅲ ) \(a>4\) のとき$$~~~21-8a~~~(x=4)$$
詳しい解説ページはこちらから↓

定義域が変化する2次関数の最大値・最小値
[ 解答を見る ]
【解答】
最大値が
( ⅰ ) \(0 < a < 4\) のとき$$~~~3~~~(x=0)$$( ⅱ ) \(a=4\) のとき$$~~~3~~~(x=0~,~a)$$( ⅲ ) \(a>4\) のとき$$~~~a^2-4a+3~~~(x=a)$$最小値が
( ⅰ ) \(0 < a < 2\) のとき$$~~~a^2-4a+3~~~(x=a)$$( ⅱ ) \(a≧2\) のとき$$~~~-1~~~(x=2)$$
詳しい解説ページはこちらから↓


2次方程式の解
[ 解答を見る ]
【解答】$${\small (1)}~x=-1~,~5$$$${\small (2)}~x=\frac{1}{2}~,~-3$$$${\small (3)}~x=\frac{5\pm\sqrt{17}}{4}$$$${\small (4)}~x=2\pm\sqrt{3}$$
詳しい解説ページはこちらから↓


2次方程式の解の個数
[ 解答を見る ]
【解答】
\({\small (1)}\) 解なし
\({\small (2)}\) 重解
\({\small (3)}\) 異なる2つの実数解
詳しい解説ページはこちらから↓


2次方程式の解の条件
\({\small (1)}\) 次の2次方程式が2つの実数解をもつとき、\(k\) の値の範囲を求めよ。$$~~~x^2-2x+k-2=0$$\({\small (2)}\) 次の2次方程式が重解をもつとき、\(k\) の値を求めよ。$$~~~4x^2-12x+2k+5=0$$
[ 解答を見る ]
【解答】$${\small (1)}~k<3$$$${\small (2)}~k=2$$
詳しい解説ページはこちらから↓


解が与えられた2次方程式
[ 解答を見る ]
【解答】$$~~~k=-3~,~x=-\frac{3}{2}$$
詳しい解説ページはこちらから↓


2次方程式の文章問題
[ 解答を見る ]
【解答】$$~~~x=6$$
詳しい解説ページはこちらから↓


2次関数とx軸との交点
[ 解答を見る ]
【解答】
\({\small (1)}\) \(x\) 軸と異なる2点で交わる。$$~~~\left(\frac{1}{3}~,~0\right)~,~(2~,~0)$$
\({\small (2)}\) \(x\) 軸と交わらない。
\({\small (3)}\) \(x\) 軸と異なる1点で交わる。(\(x\) 軸と接する。)$$~~~(3~,~0)$$
詳しい解説ページはこちらから↓


2次関数とx軸との交点の条件
\({\small (1)}\) 次の2次関数が \(x\) 軸と2点で交わるとき、\(k\) の値の範囲を求めよ。$$~~~y=x^2-(2k-1)x+k^2$$\({\small (2)}\) 次の2次関数が \(x\) 軸と接するとき、\(k\) の値と接点の座標を求めよ。$$~~~y=x^2-2kx+7k-6$$
[ 解答を見る ]
【解答】$${\small (1)}~k<\frac{1}{4}$$$${\small (2)}~k=1~,~x=1$$または$$~~~k=6~,~x=6$$
詳しい解説ページはこちらから↓


放物線と直線の交点
\({\small (1)}\) 次の放物線と直線との交点の座標を求めよ。$$~~~\biggl\{ \begin{eqnarray} y=x^2+5x-5 \\ y=2x+5 \end{eqnarray}$$\({\small (2)}\) 次の放物線と直線が接するとき、\(k\) の値と接点の座標を求めよ。$$~~~\biggl\{ \begin{eqnarray} y=x^2+5x-5 \\ y=x-k \end{eqnarray}$$
[ 解答を見る ]
【解答】$${\small (1)}~(-5~,~-5)~,~(2~,~9)$$$${\small (2)}~k=9~,~(-2~,~-11)$$
詳しい解説ページはこちらから↓

2次不等式の解①(因数分解)
[ 解答を見る ]
【解答】$${\small (1)}~-1<x<2$$$${\small (2)}~x≦-3~,~5≦x$$$${\small (3)}~x<-6~,~-1<x$$$${\small (4)}~-7≦x≦0$$
詳しい解説ページはこちらから↓


2次不等式の解②(x軸と接する)
[ 解答を見る ]
【解答】
\({\small (1)}\) 解なし
\({\small (2)}\) すべての実数
\({\small (3)}\) \(x=2\)
\({\small (4)}\) \(x=2\) 以外のすべての実数
詳しい解説ページはこちらから↓


2次不等式の解③(解の公式)
[ 解答を見る ]
【解答】$${\small (1)}~-1-\sqrt{3}<x<-1+\sqrt{3}$$$${\small (2)}~x≦\frac{3-\sqrt{17}}{4}~,~\frac{3+\sqrt{17}}{4}≦x$$$${\small (3)}~\frac{3-\sqrt{5}}{2}< x < \frac{3+\sqrt{5}}{2}$$
詳しい解説ページはこちらから↓


2次不等式の解④(交点がない)
[ 解答を見る ]
【解答】
\({\small (1)}\) すべての実数
\({\small (2)}\) 解なし
\({\small (3)}\) 解なし
\({\small (4)}\) すべての実数
詳しい解説ページはこちらから↓

連立2次不等式の解
[ 解答を見る ]
【解答】$${\small (1)}~-5≦x<-3~,~0< x≦1$$$${\small (2)}~-\frac{3}{2}≦x<1~,~1< x≦3$$
詳しい解説ページはこちらから↓


絶対不等式
[ 解答を見る ]
【解答】$$~~~-2<k<6$$
詳しい解説ページはこちらから↓


2次不等式の文章問題
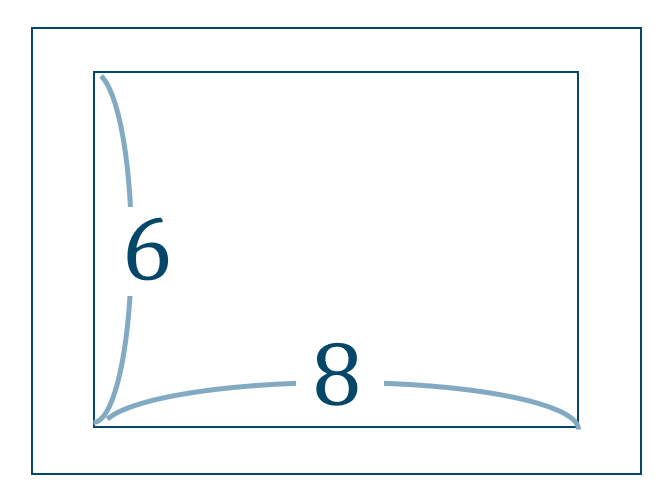

このとき、道を含めた全体の面積が \(80~m^2\) 以上 \(168~m^2\) 以下になるためには道の幅を何 \(m\) の範囲にすればよいか答えよ。
[ 解答を見る ]
【解答】
\(1~m\) 以上、\(3~m\) 以下にすればよい
詳しい解説ページはこちらから↓


2次方程式の解の符号(2次関数)
\({\small (1)}~\) 2つの解がともに正
\({\small (2)}~\) 2つの解がともに負
\({\small (3)}~\) 異符号の解
[ 解答を見る ]
【解答】$${\small (1)}~1<k<\frac{5}{4}$$$${\small (2)}~k<-5$$$${\small (3)}~k>\frac{5}{4}$$
詳しい解説ページはこちらから↓