このページは「高校数学Ⅱ:三角関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう!
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします!
【問題一覧】数学Ⅱ:三角関数
動径と一般角
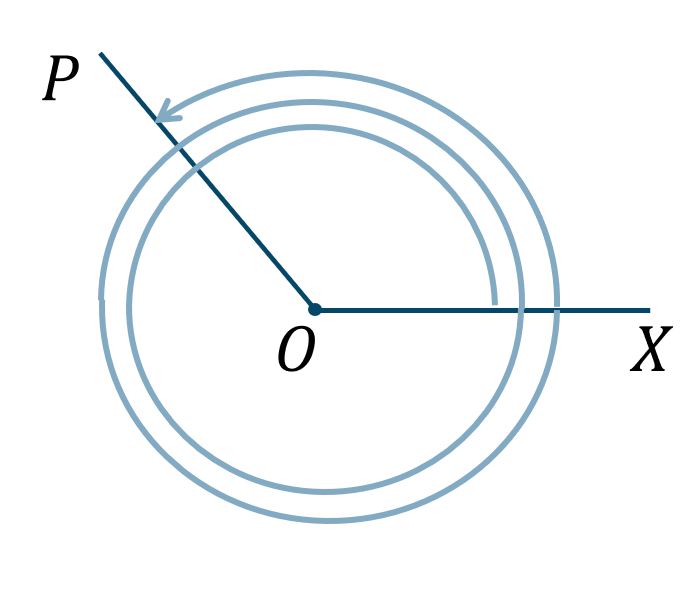
問題次の角の動径を図示せよ。また、この角の動径を表す最小の正の角を求めよ。$${\small (1)}~400^\circ$$$${\small (2)}~850^\circ$$$${\small (3)}~-600^\circ$$
[ 解答を見る ]
【解答】\({\small (1)}\)

また、この動径の最小の正の角は \(40^\circ\)
\({\small (2)}\)

また、この動径の最小の正の角は \(130^\circ\)
\({\small (3)}\)

また、この動径の最小の正の角は \(120^\circ\)
詳しい解説ページはこちらから↓

動径と一般角
今回は360°以上の角や負の角を考えるための一般角とその表し方の動径について解説していきます。それぞれ覚えておきましょう。
弧度法と扇形
問題次の問いに答えよ。
\({\small (1)}\) 次の角を弧度法で表せ。$$~{\large ①}~120^\circ~~~~~{\large ②}~750^\circ~~~~~{\large ③}~-72^\circ$$\({\small (2)}\) 次の角を度数法で表せ。$$~{\large ①}~\frac{3}{4}\pi~~~~~{\large ②}~\frac{7}{2}\pi~~~~~{\large ③}~-\frac{11}{5}\pi$$\({\small (3)}\) 半径 \(2\)、中心角 \({\large \frac{\pi}{4}}\) である扇形の弧の長さと面積を求めよ。
\({\small (4)}\) 半径 \(3\)、弧の長さ \({\large \frac{6}{5}}\pi \) である扇形の中心角と面積を求めよ。
[ 解答を見る ]
【解答】$${\small (1)}~{\large ①}~\frac{2}{3}\pi~~~{\large ②}~\frac{25}{6}\pi~~~{\large ③}~-\frac{2}{5}\pi$$$${\small (2)}~{\large ①}~135^\circ~~~{\large ②}~630^\circ~~~{\large ③}~-396^\circ$$$${\small (3)}~l=\frac{\pi}{2}~,~S=\frac{\pi}{2}$$$${\small (4)}~x=\frac{2}{5}\pi~,~S=\frac{9}{5}\pi$$
詳しい解説ページはこちらから↓

弧度法と扇形
今回は角の新しい表し方の弧度法と扇形の弧の長さと面積について解説していきます。三角関数では今後弧度法を用いて表していきますので、しっかりと理解しておきましょう。
三角関数の値(単位円)
問題\(\theta\) が次の角のとき、\(\sin{\theta}\) \(,\) \(\cos{\theta}\) \(,\) \(\tan{\theta}\) の値を求めよ。$${\small (1)}~\frac{5}{6}\pi\hspace{ 20 pt}{\small (2)}~\frac{5}{3}\pi\hspace{ 25 pt}{\small (3)}~\frac{5}{4}\pi$$$${\small (4)}~\frac{3}{2}\pi\hspace{ 20 pt}{\small (5)}~\frac{13}{6}\pi\hspace{ 20 pt}{\small (6)}~-\frac{4}{3}\pi$$
[ 解答を見る ]
【解答】左から順に \(\sin{}~,~\cos{}~,~\tan{}\) とします。$${\small (1)}~\frac{1}{2}~,~-\frac{\sqrt{3}}{2}~,~-\frac{1}{\sqrt{3}}$$$${\small (2)}~-\frac{\sqrt{3}}{2}~,~\frac{1}{2}~,~-\sqrt{3}$$$${\small (3)}~-\frac{1}{\sqrt{2}}~,~-\frac{1}{\sqrt{2}}~,~1$$$${\small (4)}~-1~,~0~,~×$$$${\small (5)}~\frac{1}{2}~,~\frac{\sqrt{3}}{2}~,~\frac{1}{\sqrt{3}}$$$${\small (6)}~\frac{\sqrt{3}}{2}~,~-\frac{1}{2}~,~-\sqrt{3}$$
詳しい解説ページはこちらから↓

三角関数の値(単位円)
弧度法で角が与えられたときの三角関数の値の求め方を解説していきます。単位円を用いて求めることができるようになりましょう。また、
三角関数の相互関係の公式
問題次の問いに答えよ。
\({\small (1)}\) \(\cos{\theta}={\large \frac{3}{5}}\) のとき、\(\sin{\theta}~,~\tan{\theta}\) の値をそれぞれ求めよ。
\({\small (2)}\) \(\tan{\theta}=-3\) のとき、\(\sin{\theta}~,~\cos{\theta}\) の値をそれぞれ求めよ。
[ 解答を見る ]
【解答】$${\small (1)}~\sin{\theta}=\frac{4}{5}~,~\tan{\theta}=\frac{4}{3}$$ または、$$~~~\sin{\theta}=-\frac{4}{5}~,~\tan{\theta}=-\frac{4}{3}$$$${\small (2)}~\cos{\theta}=\frac{1}{\sqrt{10}}~,~\sin{\theta}=-\frac{3}{\sqrt{10}}$$ または、$$~~~\cos{\theta}=-\frac{1}{\sqrt{10}}~,~\sin{\theta}=\frac{3}{\sqrt{10}}$$
詳しい解説ページはこちらから↓

三角関数の相互関係の公式
三角関数の相互関係の公式について解説していきます。与えられた三角関数の種類によって公式を使い分けましょう。
三角関数の式の値
問題\(\sin{\theta}+\cos{\theta}={\large \frac{\sqrt{2}}{2}}\) のとき、次の式の値を求めよ。$${\small (1)}~\sin{\theta}\cos{\theta}$$$${\small (2)}~\sin^3{\theta}+\cos^3{\theta}$$
[ 解答を見る ]
【解答】$${\small (1)}~\sin{\theta}\cos{\theta}=-\frac{1}{4}$$$${\small (2)}~\sin^3{\theta}+\cos^3{\theta}=\frac{5\sqrt{2}}{8}$$
詳しい解説ページはこちらから↓

三角関数の式の値
三角関数で与えられた式の値を求める問題について解説していきます。条件式の式変形の方法を覚えておきましょう。
三角関数の等式の証明
問題次の等式を証明せよ。$${\small (1)}~\frac{\cos{\theta}}{1+\sin{\theta}}+\tan{\theta}=\frac{1}{\cos{\theta}}$$$${\small (2)}~\frac{\sin^2{\theta}-\cos^2{\theta}}{1+2\sin{\theta}\cos{\theta}}=\frac{\tan{\theta}-1}{\tan{\theta}+1}$$
[ 解答を見る ]
【解答】証明の解答は解説ページにて↓

三角関数の等式の証明
三角関数の等式の証明パターンの解説していきます。よく用いる計算パターンを覚えておきましょう。
三角関数の性質①
問題次の式の値を求めよ。$${\small (1)}~\sin{\theta}\cos{(-\theta)}+\sin{(\pi-\theta)}\cos{(\pi+\theta)}$$$${\small (2)}~\frac{\cos{(\pi-\theta)}\tan{(-\theta)}\tan{(\pi+\theta)}}{\sin{(\pi+\theta)}\tan{(\pi-\theta)}}$$
[ 解答を見る ]
【解答】$${\small (1)}~0~~~~~~{\small (2)}~1$$
詳しい解説ページはこちらから↓

三角関数の性質①
三角関数の性質の1つである負角や補角などの三角関数について解説していきます。それぞれの公式は導きだせるようになりましょう。
三角関数の性質②
問題次の式の値を求めよ。$${\small (1)}~\sin{\left(\frac{\pi}{2}-\theta\right)}\cos{\theta}-\sin{\theta}\cos{\left(\frac{\pi}{2}+\theta\right)}$$$${\small (2)}~\frac{\tan{\theta}\tan{\left({\large \frac{\pi}{2}}-\theta\right)}\sin{\left({\large \frac{\pi}{2}}+\theta\right)}}{\tan{\left({\large \frac{\pi}{2}}+\theta\right)}\cos{\left({\large \frac{\pi}{2}}-\theta\right)}}$$
[ 解答を見る ]
【解答】$${\small (1)}~1~~~~~~{\small (2)}~-1$$
詳しい解説ページはこちらから↓

三角関数の性質②
前回に続いて今回は余角の公式などの三角関数の公式を解説していきます。単位円より公式を導きだせるようになりましょう。
三角関数のグラフ①
問題次の関数のグラフを描き、周期を答えよ。$${\small (1)}~y=\sin{\theta}$$$${\small (2)}~y=\cos{\theta}$$$${\small (3)}~y=\tan{\theta}$$
[ 解答を見る ]
【解答】グラフの解答は解説ページにて↓

三角関数のグラフ①
今回からは三角関数のグラフについて解説していきます。グラフの基本的な形と周期について見ていきましょう。
三角関数のグラフ②(縦幅の変化)
問題次の関数のグラフを描き、周期を答えよ。$${\small (1)}~y=\frac{1}{2}\sin{\theta}$$$${\small (2)}~y=2\cos{\theta}$$$${\small (3)}~y=-\tan{\theta}$$
[ 解答を見る ]
【解答】グラフの解答は解説ページにて↓

三角関数のグラフ②(縦幅の変化)
前回に続いて三角関数のグラフについて解説していきます。今回は縦幅の変化について見ていきましょう。
三角関数のグラフ③(周期の変化)
問題次の関数のグラフを描き、周期を答えよ。$${\small (1)}~y=\sin{2\theta}$$$${\small (2)}~y=\cos{\frac{\theta}{2}}$$$${\small (3)}~y=\tan{\frac{\theta}{2}}$$
[ 解答を見る ]
【解答】グラフの解答は解説ページにて↓

三角関数のグラフ③(周期の変化)
今回は三角関数の横の変化について解説していきます。どのように変化するかと周期の変化に注意しましょう。
三角関数のグラフ④(平行移動)
問題次の関数のグラフを描き、周期を答えよ。$${\small (1)}~y=\sin{\left(\theta-\frac{\pi}{2}\right)}$$$${\small (2)}~y=\cos{\left(\theta+\frac{\pi}{6}\right)}$$$${\small (3)}~y=\tan{\left(\theta-\frac{\pi}{4}\right)}$$
[ 解答を見る ]
【解答】グラフの解答は解説ページにて↓

三角関数のグラフ④(平行移動)
今回は三角関数のグラフの平行移動について解説していきます。どのように移動するかを確認してグラフを描きましょう。
三角関数のグラフ⑤(式変形)
問題次の関数のグラフを描き、周期を答えよ。$${\small (1)}~y=\sin{\left( \frac{1}{2}\theta-\frac{\pi}{6} \right)}$$$${\small (2)}~y=\cos{(2\theta+\pi)}$$
[ 解答を見る ]
【解答】グラフの解答は解説ページにて↓

三角関数のグラフ⑤(式変形)
今回は式変形の必要な三角関数のグラフについて解説していきます。式変形の方法を覚えておきましょう。
三角関数を含む方程式①
問題次の方程式の解を求めよ。ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~\sin{\theta}=-\frac{\sqrt{3}}{2}$$$${\small (2)}~\sqrt{2} \cos{\theta}-1=0$$$${\small (3)}~\tan{\theta}+1=0$$
[ 解答を見る ]
【解答】$${\small (1)}~\theta=\frac{4}{3}\pi~,~\frac{5}{3}\pi$$$${\small (2)}~\theta=\frac{\pi}{4}~,~\frac{7}{4}\pi$$$${\small (3)}~\theta=\frac{3}{4}\pi~,~\frac{7}{4}\pi$$
詳しい解説ページはこちらから↓

三角関数を含む方程式①
三角関数を含む方程式について解説していきます。範囲に注意して単位円を用いて解いていきましょう。
三角関数を含む方程式②(範囲変化)
問題次の方程式を求めよ。ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~\sin{\left(\theta+\frac{\pi}{4}\right)}=\frac{1}{2}$$$${\small (2)}~\cos{\left(\theta-\frac{\pi}{4}\right)}=\frac{\sqrt{3}}{2}$$
[ 解答を見る ]
【解答】$${\small (1)}~\theta=\frac{7}{12}\pi~,~\frac{23}{12}\pi$$$${\small (2)}~\theta=\frac{\pi}{12}~,~\frac{5}{12}\pi$$
詳しい解説ページはこちらから↓

三角関数を含む方程式②(範囲変化)
θの値の範囲が変化するパターンの三角関数を含む方程式について解説していきます。
三角関数を含む不等式①
問題次の不等式の解を求めよ。ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~\sin{\theta}≦-\frac{\sqrt{3}}{2}$$$${\small (2)}~\cos{\theta}>\frac{1}{2}$$$${\small (3)}~\tan{\theta}≧-1$$
[ 解答を見る ]
【解答】$${\small (1)}~\frac{4}{3}\pi≦\theta≦\frac{5}{3}\pi$$$${\small (2)}~0≦\theta<\frac{\pi}{3}~,~\frac{5}{3}\pi<\theta<2\pi$$$${\small (3)}~0≦\theta<\frac{\pi}{2}~,~\frac{3}{4}\pi≦\theta<\frac{3}{2}\pi~,~\frac{7}{4}\pi≦\theta<2\pi$$
詳しい解説ページはこちらから↓

三角関数を含む不等式①
三角関数を含む不等式について解説していきます、方程式のときと同様に単位円を用いて視覚的に解きましょう。
三角関数を含む不等式②(範囲変化)
問題次の不等式の解を求めよ。ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~\sin{\left(\theta+\frac{\pi}{4}\right)}≧\frac{1}{2}$$$${\small (2)}~\cos{\left(\theta-\frac{\pi}{3}\right)}>\frac{1}{\sqrt{2}}$$$${\small (3)}~\tan{\left(\theta-\frac{\pi}{4}\right)}≦\sqrt{3}$$
[ 解答を見る ]
【解答】$${\small (1)}~ 0≦\theta≦\frac{7}{12}\pi~,~ \frac{23}{12}\pi≦\theta<2\pi$$$${\small (2)}~\frac{\pi}{12}<\theta<\frac{7}{12}\pi$$$${\small (3)}~ 0≦\theta≦\frac{7}{12}\pi~,~ \frac{3}{4}\pi<\theta≦\frac{19}{12}\pi$$$$~~~~~\frac{7}{4}\pi<\theta<2\pi$$
詳しい解説ページはこちらから↓

三角関数を含む不等式②(範囲変化)
今回は範囲が変化するパターンの三角関数を含む不等式について解説していきます。
三角関数を含む2次方程式
問題次の2次方程式の解を求めよ。ただし、\(0≦\theta<2\pi\) とする。$${\small (1)}~2\sin{\theta}\cos{\theta}+2\sin{\theta}-\cos{\theta}-1=0$$$${\small (2)}~2\sin^2{\theta}-3\cos{\theta}-3=0$$
[ 解答を見る ]
【解答】$${\small (1)}~\theta=\frac{\pi}{6}~,~\frac{5}{6}\pi~,~\pi$$$${\small (2)}~\theta=\frac{2}{3}\pi~,~\pi~,~\frac{4}{3}\pi$$
詳しい解説ページはこちらから↓

三角関数を含む2次方程式
今回からは三角関数を含む2次式について解説していきます。2次方程式となるときは、三角関数の値を別の文字に置き換えて考えましょう。
三角関数を含む2次不等式
問題次の不等式の解を求めよ。ただし、\(0≦\theta<2\pi\) とする。$$~~~2\cos^2{\theta}-\sin{\theta}-1≧0$$
[ 解答を見る ]
【解答】$$~~~0≦\theta≦\frac{\pi}{6}~,~\frac{5}{6}\pi≦\theta<2\pi$$
詳しい解説ページはこちらから↓

三角関数を含む2次不等式
今回は三角関数を含む2次不等式について解説していきます。方程式のときと同様に文字に置き換えて解いていきましょう。
三角関数を含む2次関数
問題次の関数の最大値と最小値を求め、そのときの \(\theta\) の値も求めよ。ただし、\(0≦\theta<2\pi\) とする。$$~~~y=\sin^2{\theta}+\cos{\theta}+1$$
[ 解答を見る ]
【解答】
最大値が$$~~~\frac{9}{4}~~~\left(\theta=\frac{\pi}{3}~,~\frac{5}{3}\pi\right)$$最小値が$$~~~0~~~(\theta=\pi)$$
詳しい解説ページはこちらから↓

三角関数を含む2次関数
三角関数を含む2次関数の最大値・最小値についての問題を解説していきます。三角関数を文字で置き換えるとき、値の範囲に注意しましょう。
加法定理
問題次の三角関数の値を求めよ。$${\small (1)}~\sin{75^\circ}$$$${\small (2)}~\cos{165^\circ}$$$${\small (3)}~\tan{15^\circ}$$$${\small (4)}~\sin{\frac{\pi}{12}}$$$${\small (5)}~\cos{\frac{7}{12}\pi}$$$${\small (6)}~\tan{\frac{5}{12}\pi}$$
[ 解答を見る ]
【解答】$${\small (1)}~\frac{\sqrt{6}+\sqrt{2}}{4}$$$${\small (2)}~-\frac{\sqrt{6}+\sqrt{2}}{4}$$$${\small (3)}~ 2-\sqrt{3}$$$${\small (4)}~ \frac{\sqrt{6}-\sqrt{2}}{4}$$$${\small (5)}~ \frac{\sqrt{2}-\sqrt{6}}{4}$$$${\small (6)}~ 2+\sqrt{3}$$
詳しい解説ページはこちらから↓

加法定理
今回は加法定理について解説していきます。三角関数の重要公式となりますので、しっかりと覚えておきましょう。また、有名角以外の角の導き方も押さえておきましょう。
加法定理と式の値
問題下の条件のとき、次の式の値を求めよ。ただし、\(\alpha\) は第3象限、\(\beta\) は第4象限の角とする。$$~~~~~\sin{\alpha}=-\frac{3}{5}~,~\cos{\beta}=\frac{1}{3}$$$${\small (1)}~\sin{(\alpha+\beta)}$$$${\small (2)}~\cos{(\alpha-\beta)}$$
[ 解答を見る ]
【解答】$${\small (1)}~ \frac{8\sqrt{2}-3}{15}$$$${\small (2)}~ \frac{6\sqrt{2}-4}{15}$$
詳しい解説ページはこちらから↓

加法定理と式の値
今回は加法定理を用いて式の値を計算する問題について解説していきます。αとβの表を用いて解いていきましょう。
2直線のなす角
問題次の2直線のなす角を求めよ。ただし、\(\theta\) は鋭角とする。$$~~~y=-\frac{\sqrt{3}}{5}x+2~,~y=\frac{\sqrt{3}}{2}x+1$$
[ 解答を見る ]
【解答】$$~~~\frac{\pi}{3}$$
詳しい解説ページはこちらから↓

2直線のなす角
今回は座標平面上における2直線のなす角について解説していきます。傾きの値と正接の加法定理より、なす角を求めましょう。
2倍角の公式
問題下の条件のとき、次の式の値を求めよ。$$~~~\sin{\alpha}=\frac{3}{5}~~~\left(\frac{\pi}{2}<\alpha<\pi\right)$$$${\small (1)}~\sin{2\alpha}$$$${\small (2)}~\cos{2\alpha}$$$${\small (3)}~\tan{2\alpha}$$
[ 解答を見る ]
【解答】$${\small (1)}~ -\frac{24}{25}$$$${\small (2)}~ \frac{7}{25}$$$${\small (3)}~ -\frac{24}{7}$$
詳しい解説ページはこちらから↓

2倍角の公式
今回は2倍角の公式について解説していきます。公式を覚えるだけでなく、公式の作り方と使い方も合わせて覚えておきましょう。
半角の公式
問題下の条件のとき、次の式の値を求めよ。$$~~~\sin{\alpha}=\frac{3}{5}~~~\left(\frac{\pi}{2}<\alpha<\pi\right)$$$${\small (1)}~\sin{\frac{\alpha}{2}}$$$${\small (2)}~\cos{\frac{\alpha}{2}}$$$${\small (3)}~\tan{\frac{\alpha}{2}}$$
[ 解答を見る ]
【解答】$${\small (1)}~ \frac{3}{\sqrt{10}}$$$${\small (2)}~ \frac{1}{\sqrt{10}}$$$${\small (3)}~ 3$$
詳しい解説ページはこちらから↓

半角の公式
今回は半角の公式について解説していきます。公式の導き方だけでなく、公式を使う上での注意点と答え方も押さえておきましょう。
2倍角を含む方程式・不等式
問題次の方程式、不等式の解を求めよ。ただし、\(0≦x<2\pi\) とする。$${\small (1)}~\sin{2x}-\cos{x}=0$$$${\small (2)}~\cos{2x}-3\cos{x}+2≦0$$
[ 解答を見る ]
【解答】$${\small (1)}~x=\frac{\pi}{6}~,~\frac{\pi}{2}~,~\frac{5}{6}\pi~,~\frac{3}{2}\pi$$$${\small (2)}~ 0≦x≦\frac{\pi}{3}~,~\frac{5}{3}\pi≦x<2\pi$$
詳しい解説ページはこちらから↓

2倍角を含む方程式・不等式
今回は2倍角を含む方程式・不等式について解説していきます。公式の使い方からその後の計算方法まで押さえておきましょう。
三角関数の合成
問題次の式を合成せよ。$${\small (1)}~\sin{\theta}+\sqrt{3}\cos{\theta}$$$${\small (2)}~\sqrt{3}\sin{\theta}-\cos{\theta}$$$${\small (3)}~\cos{\theta}-\sin{\theta}$$
[ 解答を見る ]
【解答】$${\small (1)}~ 2\sin{\left(\theta+\frac{\pi}{3}\right)}$$$${\small (2)}~ 2\sin{\left(\theta-\frac{\pi}{6}\right)}$$$${\small (3)}~ \sqrt{2}\sin{\left(\theta+\frac{3}{4}\pi\right)}$$
詳しい解説ページはこちらから↓

三角関数の合成
三角関数の合成について解説していきます。公式として覚えるのではなく、手順として計算方法と角度の求め方を覚えておきましょう。
合成を用いる方程式・不等式
問題次の方程式・不等式の解を求めよ。ただし、\(0≦x<2\pi\) とする。$${\small (1)}~\sin{x}+\sqrt{3}\cos{x}=\sqrt{3}$$$${\small (2)}~\sqrt{2}\sin{x}-\sqrt{6}\cos{x}≦2$$
[ 解答を見る ]
【解答】$${\small (1)}~x=0~,~\frac{\pi}{3}$$$${\small (2)}~ 0≦x≦\frac{7}{12}\pi~,~\frac{13}{12}\pi≦x<2\pi$$
詳しい解説ページはこちらから↓

合成を用いる方程式・不等式
今回は三角関数の合成を用いて方程式・不等式を解く問題について解説していきます。合成後の範囲に注意して計算しましょう。
三角関数の最大値・最小値
問題次の関数の最大値と最小値を求めよ。ただし、\(0≦x<2\pi\) とする。$${\small (1)}~y=-\cos{2x}+2\sin{x}-1$$$${\small (2)}~y=2\sin{x}+2\cos{x}$$
[ 解答を見る ]
【解答】
\({\small (1)}\) 最大値は、$$~~~~2~~~\left(x=\frac{\pi}{2}\right)$$最小値は、$$~~~-\frac{5}{2}~~~\left(x=\frac{7}{6}\pi~,~\frac{11}{6}\pi\right)$$\({\small (2)}\) 最大値は、$$~~~~2\sqrt{2}~~~\left(x=\frac{\pi}{4}\right)$$最小値は、$$~~~-2\sqrt{2}~~~\left(x=\frac{5}{4}\pi\right)$$
詳しい解説ページはこちらから↓

三角関数の最大値・最小値
三角関数の最大値・最小値について解説していきます。2倍角の公式を用いるパターンと合成を用いるパターンをそれぞれの解法を覚えておきましょう。