【問題一覧】数学Ⅱ：図形と方程式

このページは「高校数学Ⅱ：図形と方程式」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。

教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします！

【問題一覧】数学Ⅱ：図形と方程式

【問題一覧】数学Ⅱ：図形と方程式

直線上の線分の長さ・内分点・外分点

問題直線上の３点 $A(-3)~,~B(1)~,~C(5)$ について次の値を求めよ。
${\small (1)}~$線分 $AB$ の長さ
${\small (2)}~$線分 $BC$ の長さ
${\small (3)}~$線分 $AB$ の中点の座標 $M$
${\small (4)}~$線分 $AC$ を $2:1$ に内分する点の座標 $P$
${\small (5)}~$線分 $BC$ を $3:1$ に外分する点の座標 $Q$

[ 解答を見る ]

【解答】$${\small (1)}~4~~~~~~{\small (2)}~4~~~~~~{\small (3)}~M(-1)$$$${\small (4)}~P\left( \frac{7}{3} \right)~~~~~~{\small (5)}~Q(7)$$

詳しい解説ページはこちらから↓

直線上の線分の長さ・内分点・外分点

数直線上の２点間の距離や内分点、外分点の座標について解説していきます。それぞれの解法を覚えておきましょう。

平面上の線分の長さ

問題４点 $A(2,3)~,~B(1,-1)~,~C(-2,1)~,~$ $D(k,-1)$ について、次の問いに答えよ。
${\small (1)}~$線分 $AB$ の長さ
${\small (2)}~$線分 $BC$ の長さ
${\small (3)}~$線分 $AC$ の長さ
${\small (4)}~$線分 $AD$ の長さが $5$ となるような $k$ の値

[ 解答を見る ]

【解答】$${\small (1)}~\sqrt{17}~~~~~~{\small (2)}~\sqrt{13}$$$${\small (3)}~2\sqrt{5}~~~~~~{\small (4)}~k=-1~,~5$$

詳しい解説ページはこちらから↓

平面上の線分の長さ

座標平面上の２点間の距離について解説していきます。基本は三平方の定理を用いて計算していきます。公式として覚えておきましょう。

平面上の三角形の形状

問題次の３点を頂点とする三角形はどのような三角形となるか答えよ。$${\small (1)}~A(1,4)~,~B(0,-1)~,~C(3,1)$$$${\small (2)}~A(-1,0)~,~B(2,\sqrt{3})~,~C(-1,2\sqrt{3})$$

[ 解答を見る ]

【解答】
${\small (1)}~$$BC=AC$ で $\angle {C}=90^\circ$ の直角二等辺三角形
${\small (2)}~$正三角形

詳しい解説ページはこちらから↓

平面上の三角形の形状

平面上の３点がどのような三角形になるかを調べる問題を解説していきます。２点間の距離の公式を使って考えていきましょう。

線分の長さの条件

問題３点 $A(2,3)~,~B(1,-1)~,~C(-2,1)$ について、次の点の座標を求めよ。
${\small (1)}~$２点 $A~,~B$ から等距離にある $x$ 軸上の点 $P$ の座標
${\small (2)}~$２点 $B~,~C$ から等距離にある $y=-2x+1$ 上の点 $Q$ の座標

[ 解答を見る ]

【解答】$${\small (1)}~P\left( \frac{11}{2},0\right)~~~~~~{\small (2)}~Q\left( \frac{1}{14}, \frac{6}{7}\right)$$

詳しい解説ページはこちらから↓

線分の長さの条件

２点から等距離にある点の座標を求める問題について解説していきます。解法の手順と条件の使い方。覚えておきましょう。

平面上の内分点・外分点・重心

問題３点 $A(2,3)~,~B(1,-1)~,~C(-2,1)$ について、次の点の座標を求めよ。
${\small (1)}~$線分 $AB$ の中点
${\small (2)}~$線分 $BC$ を $2:1$ に内分する点
${\small (3)}~$線分 $CA$ を $3:1$ に外分する点
${\small (4)}~$三角形 $ABC$ の重心

[ 解答を見る ]

【解答】$${\small (1)}~\left(\frac{3}{2},1\right)~~~~~~{\small (2)}~\left( -1,\frac{1}{3}\right)$$$${\small (3)}~(4,4)~~~~~~~~~~~~{\small (4)}~\left( \frac{1}{3},1\right)$$

詳しい解説ページはこちらから↓

平面上の内分点・外分点・重心

座標平面上の内分点と外分点と重心について解説していきます。直線上のときの内分点と外分点が基本となります。

点に対して対称な点

問題点 $A(2,3)$ に対して、次の点と対称な点の座標を求めよ。$${\small (1)}~(1,-1)$$$${\small (2)}~(-2,1)$$

[ 解答を見る ]

【解答】$${\small (1)}~~(3,7)$$$${\small (2)}~~(6,5)$$

詳しい解説ページはこちらから↓

点に対して対称な点

点に対して対称な点の座標を求める問題を解説していきます。点の位置関係を考えて条件式を作って解いていきましょう。

平行四辺形を作る点の座標

問題３点 $A(2,3)~,~B(1,-1)~,~C(-2,1)$ と点 $D$ の４点を結ぶと平行四辺形となるとき、点 $D$ の座標を求めよ。

[ 解答を見る ]

【解答】$$~~~~(-1,5)~,~(-3,-3)~,~(5,1)$$

詳しい解説ページはこちらから↓

平行四辺形を作る点の座標

４点が平行四辺形を作るときの問題について解説していきます。平行四辺形の性質の１つである「対角線は中点で交わる」条件を用いて解いていきましょう。

座標を利用した等式の証明

問題三角形 $ABC$ と辺 $BC$ の中点 $M$ において、次の等式が成り立つことを証明せよ。$$~~~AB^2+AC^2=2(AM^2+BM^2)$$

[ 解答を見る ]

【解答】
[証明]
線分 $BC$ の中点 $M$ を原点におき、３点 $A,B,C$ を次のように座標平面上に表します。
$$~~~A(a,b)~,~B(-c,0)~,~C(c,0)~,~M(0,0)$$
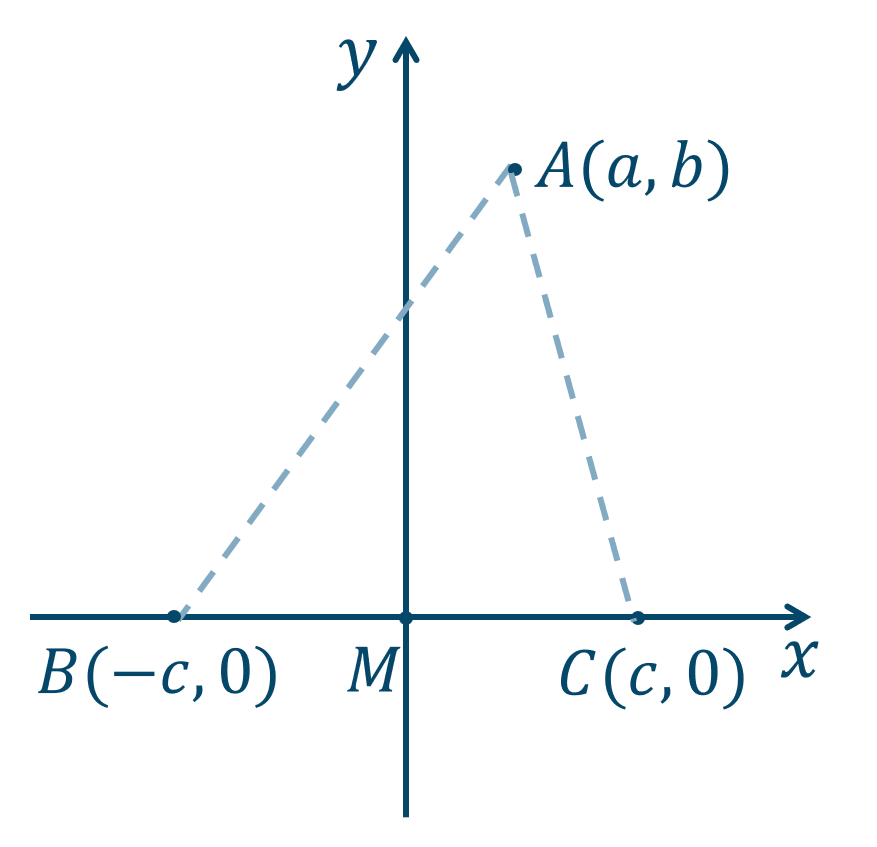
$AB$ と $AC$ の２点間の距離の公式より、$$~~~~~~AB^2$$$$~=(-c-a)^2+(0-b)^2$$$$~=c^2+2ac+a^2+b^2$$$$~=a^2+b^2+c^2+2ac$$また、$$~~~~~~AC^2$$$$~=(c-a)^2+(0-b)^2$$$$~=c^2-2ac+a^2+b^2$$$$~=a^2+b^2+c^2-2ac$$よって、$$~~~~~~AB^2+AC^2$$$$~=(a^2+b^2+c^2+2ac)$$$$\hspace{40pt}+(a^2+b^2+c^2-2ac)$$$$~=2a^2+2b^2+2c^2$$$$~=2(a^2+b^2+c^2)~\cdots①$$次に、$AM$ と $BM$ の２点間の距離の公式より、$$~~~~~~AM^2$$$$~=(0-a)^2+(0-b)^2$$$$~=a^2+b^2$$また、$$~~~~~~BM^2$$$$~=\{0-(-c)\}^2$$$$~=c^2$$よって、$$~~~~~~2(AM^2+BM^2)$$$$~=2(a^2+b^2+c^2)~\cdots②$$したがって、①と②より、$$~~~AB^2+AC^2=2(AM^2+BM^2)$$[終]

詳しい解説ページはこちらから↓

座標を利用した等式の証明

座標を利用して図形の性質を証明する問題を解説していきます。今回の「中線定理」と呼ばれる定理の証明は有名なのでそのまま証明方法を覚えておきましょう。

直線の方程式

問題次の直線の方程式を求めよ。また、一般形で表せ。
${\small (1)}~$点 $(2,3)$ を通り、$x$ 軸に平行な直線
${\small (2)}~$点 $(2,3)$ を通り、$y$ 軸に平行な直線
${\small (3)}~$傾きが $3$ で $y$ 切片が $-2$ の直線
${\small (4)}~$傾きが $3$ で、点 $(2,3)$ を通る直線

[ 解答を見る ]

【解答】$${\small (1)}~y=3~~,~~y-3=0$$$${\small (2)}~x=2~~,~~x-2=0$$$${\small (3)}~y=3x-2~~,~~3x-y-2=0$$$${\small (4)}~y=3x-3~~,~~3x-y-3=0$$

詳しい解説ページはこちらから↓

直線の方程式

今回は直線の方程式について解説していきます。条件別に直線の方程式を求めることができるようになりましょう。

２点を通る直線の方程式

問題次の直線の方程式を求めよ。
${\small (1)}~$２点 $(2,3)~,~(-2,1)$ を通る直線
${\small (2)}~$２点 $(2,3)~,~(2,-5)$ を通る直線
${\small (3)}~$２点 $(3,1)~,~(-2,1)$ を通る直線
${\small (4)}~$２点 $(2,0)~,~(0,1)$ を通る直線

[ 解答を見る ]

【解答】$${\small (1)}~y=\frac{1}{2} x+2~~~~~~{\small (2)}~x=2$$$${\small (3)}~y=1~~~~~~~~~~~~~~~~~{\small (4)}~y=-\frac{1}{2}x+1$$

詳しい解説ページはこちらから↓

２点を通る直線の方程式

前回の続きで直線の方程式について解説していきます。今回は２点を通る直線の方程式となるので、求め方を覚えておきましょう。

平行な直線と垂直な直線

問題次の直線の方程式を求めよ。
${\small (1)}~$点 $(-2,1)$ を通り、直線 $y=-3x+9$ に平行な直線と垂直な直線
${\small (2)}~$点$(2,3)$ を通り、直線 $x-5y+1=0$ に平行な直線と垂直な直線

[ 解答を見る ]

【解答】
${\small (1)}~$平行な直線の方程式は、$$~~~~~~~~y=-3x-5$$　　垂直な直線の方程式は、$$~~~~~~~~y=\frac{1}{3}x+\frac{5}{3}$$${\small (2)}~$平行な直線の方程式は、$$~~~~~~~~x-5y+13=0$$　　垂直な直線の方程式は、$$~~~~~~~~5x+y-13=0$$

詳しい解説ページはこちらから↓

平行な直線と垂直な直線

与えられた直線に対して平行な直線と垂直な直線の方程式を求める問題を解説していきます。それぞれの傾きの条件を覚えておきましょう。

直線に対して対称な点

問題直線 $l:~x-2y+7=0$ に対して点 $A(1,-1)$ と対称な点 $B$ の座標を求めよ。

[ 解答を見る ]

【解答】$$~~~~B(-3,7)$$

詳しい解説ページはこちらから↓

直線に対して対称な点

今回は直線に対して対称な点の座標を求める問題の解説をしていきます。頻出問題ですので解法の手順をしっかりと覚えておきましょう。

垂直二等分線の方程式

問題２点 $A(2,3)~,~B(-2,1)$ を結ぶ線分 $AB$ の垂直二等分線の方程式を求めよ。

[ 解答を見る ]

【解答】$$~~~~y=-2x+2$$

詳しい解説ページはこちらから↓

垂直二等分線の方程式

線分に対する垂直二等分線の方程式を求める問題について解説していきます。条件をしっかりと覚えておきましょう。

３直線が１点で交わる

問題次の３直線が１点で交わるとき、定数 $k$ の値を求めよ。$$~~~~~x+y-1=0$$$$~~~2x-y+7=0$$$$~~~kx+y+3=0$$

[ 解答を見る ]

【解答】$$~~~~k=3$$

詳しい解説ページはこちらから↓

３直線が１点で交わる

３直線が１点で交わるときの問題を解説していきます。、２直線の交点がもう１つの直線も通ることを利用して解きましょう。

２直線の交点を通る直線

問題２直線 $x+y-1=0$ $,$ $2x-3y+3=0$ の交点と点 $P(4,-1)$ を通る直線の方程式を求めよ。

[ 解答を見る ]

【解答】$$~~~~x+2y-2=0$$

詳しい解説ページはこちらから↓

２直線の交点を通る直線

２直線の交点を通る直線の方程式の求め方について解説していきます。２通りの解法をそれぞれ覚えておきましょう。

点と直線との距離

問題次の点と直線との距離を求めよ。$${\small (1)}~x-2y+4=0~,~(0,0)$$$${\small (2)}~x-2y+4=0~,~(1,5)$$$${\small (3)}~y=-\frac{3}{4}x+1~,~(2,3)$$

[ 解答を見る ]

【解答】$${\small (1)}~\frac{4\sqrt{5}}{5}~~~~~~{\small (2)}~\sqrt{5}~~~~~~{\small (3)}~\frac{14}{5}$$

詳しい解説ページはこちらから↓

点と直線との距離

座標平面上の点と直線との距離を求める問題について解説していきます。公式の使い方をしっかりと覚えておきましょう。

定点を通る直線の方程式

問題$k$ を定数とするとき、次の直線の方程式が $k$ の値が変化しても必ず定点を通る。この定点の座標を求めよ。$$~~~(k+2)x+(k-1)y-5k-1=0$$

[ 解答を見る ]

【解答】$$~~~~(2,3)$$

詳しい解説ページはこちらから↓

定点を通る直線の方程式

今回は定点を通る直線の方程式についての問題の解説していきます。パターン問題として解法の手順を覚えておきましょう。

円の方程式

問題次の問いに答えよ。
${\small (1)}~$次の円の方程式を求めよ。
　① 原点が中心で、半径 $2$ の円
　② 中心が $(1,-2)$ で、半径 $3$ の円
${\small (2)}~$次の円の中心の座標と半径を求めよ。
　① $x^2+y^2+2x-6y+6=0$
　② $x^2+y^2+4x+10y+2=0$

[ 解答を見る ]

【解答】$${\small (1)}~{\large ①}~x^2+y^2=4$$$$~~~~~{\large ②}~(x-1)^2+(y+2)^2=9$$${\small (2)}~$${\large ①}~$中心 $(-1,3)$ 、半径 $2$

$~~~~~{\large ②}~$中心 $(-2,-5)$ 、半径 $3\sqrt{3}$

詳しい解説ページはこちらから↓

円の方程式

座標平面上の円を方程式で表す問題について解説していきます。円の方程式の２つの形を覚えておきましょう。

円の方程式の決定①（点の条件）

問題次の円の方程式を求めよ。
${\small (1)}~$２点 $A(-3,6)~,~B(3,-2)$ が直径
${\small (2)}~$３点 $(0,1)~,~(-2,-1)~,~(-4,1)$ を通る

[ 解答を見る ]

【解答】$${\small (1)}~x^2+(y-2)^2=25$$$${\small (2)}~x^2+y^2+4x-2y+1=0$$

詳しい解説ページはこちらから↓

円の方程式の決定①（点の条件）

通る点が条件として与えられたときの円の方程式の求め方を解説していきます。それぞれのパターンを覚えておきましょう。

円の方程式の決定②（接する条件）

問題次の円の方程式を求めよ。
${\small (1)}~$点 $(1,-2)$ を中心として、$x$ 軸に接する円
${\small (2)}~$点 $(1,-2)$ を中心として、$y$ 軸に接する円
${\small (3)}~$点 $(2,1)$ を中心として、直線 $2x-y+2=0$ に接する円

[ 解答を見る ]

【解答】$${\small (1)}~(x-1)^2+(y+2)^2=4$$$${\small (2)}~(x-1)^2+(y+2)^2=1$$$${\small (3)}~(x-2)^2+(y-1)^2=5$$

詳しい解説ページはこちらから↓

円の方程式の決定②（接する条件）

円と接する条件があるときの円の方程式を求める問題を解説していきます。それぞれの場合の条件を考えて半径を求めましょう。

円の方程式を表す条件

問題次の方程式が円の方程式を表すような、実数 $k$ の値の範囲を求めよ。$$~~~x^2+y^2+4x-2y+k+3=0$$

[ 解答を見る ]

【解答】$$~~~~k<2$$

詳しい解説ページはこちらから↓

円の方程式を表す条件

円の方程式となるかの条件について解説していきます。条件に合わないときはどうなるかも含めて覚えておきましょう。

円と直線との共有点

問題次の円と直線との共有点の個数と、その共有点の座標を求めよ。$${\small (1)}~\biggl\{ \begin{eqnarray} ~x^2+y^2=5 \\ ~3x-y+5=0\end{eqnarray}$$$${\small (2)}~\biggl\{ \begin{eqnarray} ~x^2+y^2=5 \\ ~2x-y-5=0\end{eqnarray}$$

[ 解答を見る ]

【解答】
${\small (1)}~$異なる２点で交わり、その座標は、$$~~~(x,y)=(-1,2)~,~(-2,-1)$$${\small (2)}~$接して、その座標は、$$~~~(x,y)=(2,-1)$$

詳しい解説ページはこちらから↓

円と直線との共有点

円と直線との共有点について解説していきます。共有点の個数の調べ方と共有点の座標の求め方を覚えておきましょう。

円と直線との位置関係

問題次の問いに答えよ。
${\small (1)}~$円 $x^2+y^2=10$ と直線 $y=3x+k$ が２点で交わるとき、実数 $k$ の値の範囲を求めよ。
${\small (2)}~$円 $x^2+y^2=r^2$ と直線 $y=-2x+1$ が接するとき、実数 $r$ の値を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~-10<k<10$$$${\small (2)}~r=\frac{\sqrt{5}}{5}$$

詳しい解説ページはこちらから↓

円と直線との位置関係

円と直線との位置関係の条件についての問題を解説していきます。解法が２つあり、１つは前回の判別式を利用して解きますので復習しておきましょう。

円によって切り取られる線分

問題直線 $x-y-1=0$ が円 $x^2+y^2=4$ によって切り取られてできた線分の長さを求めよ。

[ 解答を見る ]

【解答】$$~~~~\sqrt{14}$$

詳しい解説ページはこちらから↓

円によって切り取られる線分

直線が円によって切り取られる線分すなわち弦の長さの求め方について解説していきます。点と直線との距離の公式と三平方の定理を用いて解いていきましょう。

円の接線の方程式

問題次の問いに答えよ。
${\small (1)}~$円 $x^2+y^2=5$ 上の点 $(-1,2)$ における接線の方程式を求めよ。
${\small (2)}~$円 $x^2+y^2=10$ に点 $(5,5)$ から引いた接線の方程式を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~x-2y+5=0$$$${\small (2)}~x-3y+10=0~,~3x-y-10=0$$

詳しい解説ページはこちらから↓

円の接線の方程式

円に対して接する直線の方程式について解説していきます。公式を用いて求めることができるので、まずは公式を覚えておきましょう。

２つの円の位置関係

問題下の２つの円 $C_1$ と円 $C_2$ が次の位置関係のとき、$r$ の値または範囲を求めよ。$$~~~\biggl\{ \begin{eqnarray} ~(x-3)^2+(y-4)^2=4~\cdots {\small (C_1)} \\ ~x^2+y^2=r^2~\cdots{\small (C_2)} \end{eqnarray}$$${\small (1)}~$外接する
${\small (2)}~$内接する
${\small (3)}~$離れている
${\small (4)}~$内部にある
${\small (5)}~$２点で交わる

[ 解答を見る ]

【解答】$${\small (1)}~r=3~~~~~~{\small (2)}~r=7~~~~~~{\small (3)}~r<3$$$${\small (4)}~r>7~~~~~~{\small (5)}~3<r<7$$

詳しい解説ページはこちらから↓

２つの円の位置関係

２つの円の位置関係について解説していきます。５つの位置関係とその条件を覚えておきましょう。

２つの円の共有点の座標

問題次の２つの円の共有点の座標を求めよ。$$~~~\biggl\{ \begin{eqnarray} ~x^2+y^2+x-2y-5=0 \\~x^2+y^2=10 \end{eqnarray}$$

[ 解答を見る ]

【解答】$$~~~~(x,y)=(-3,1)~,~(1,3)$$

詳しい解説ページはこちらから↓

２つの円の共有点の座標

２つの共有点の座標の求め方を解説していきます。そのまま連立するだけでは解けないので、解法の手順を覚えておきましょう。

２つの円の交点を通る円・直線

問題次の２つの円の交点を通り、点 $(2,3)$ を通る円の方程式を求めよ。また、この２つの円の交点を通る直線の方程式を求めよ。$$~~~\biggl\{ \begin{eqnarray} ~x^2+y^2=5 \\~x^2+y^2-2x-6y+1=0 \end{eqnarray}$$

[ 解答を見る ]

【解答】$$~~~~x+3y-3=0$$

詳しい解説ページはこちらから↓

２つの円の交点を通る円・直線

２つの円の交点を通る円の方程式と直線の方程式について解説していきます。交点の座標を求めなくても円の方程式を求めることができます。その方法を覚えておきましょう。

軌跡①

問題２点 $A(-2,0)~,~B(3,0)$ からの距離の比が $3:2$ である点 $P$ の軌跡を求めよ。

[ 解答を見る ]

【解答】
　中心 $(7,0)$、半径 $6$ の円

詳しい解説ページはこちらから↓

軌跡①

与えられた条件を満たす点が動いてできる図形を軌跡といいます。この軌跡を求める手順を解説していきます。

軌跡②（動点を含む）

問題ある点 $Q$ が放物線 $y=x^2+1$ 上を動くとき、点 $A(2,-3)$ と点 $Q$ を結ぶ線分の中点 $P$ の軌跡を求めよ。

[ 解答を見る ]

【解答】
　放物線 $y=2x^2-4x+1$

詳しい解説ページはこちらから↓

軌跡②（動点を含む）

今回は軌跡の問題について、条件に別の動点を含む問題を解説していきます。今回のパターンも手順を覚えておきましょう。

不等式の表す領域

問題次の不等式の表す領域を求めよ。$${\small (1)}~y≦-2x+3$$$${\small (2)}~x<3$$$${\small (3)}~y≦-1$$$${\small (4)}~x^2+y^2≧5$$$${\small (5)}~y<-x^2+2x$$

[ 解答を見る ]

【解答】
${\small (1)}~$下の図の斜線部分となり、境界線を含む。

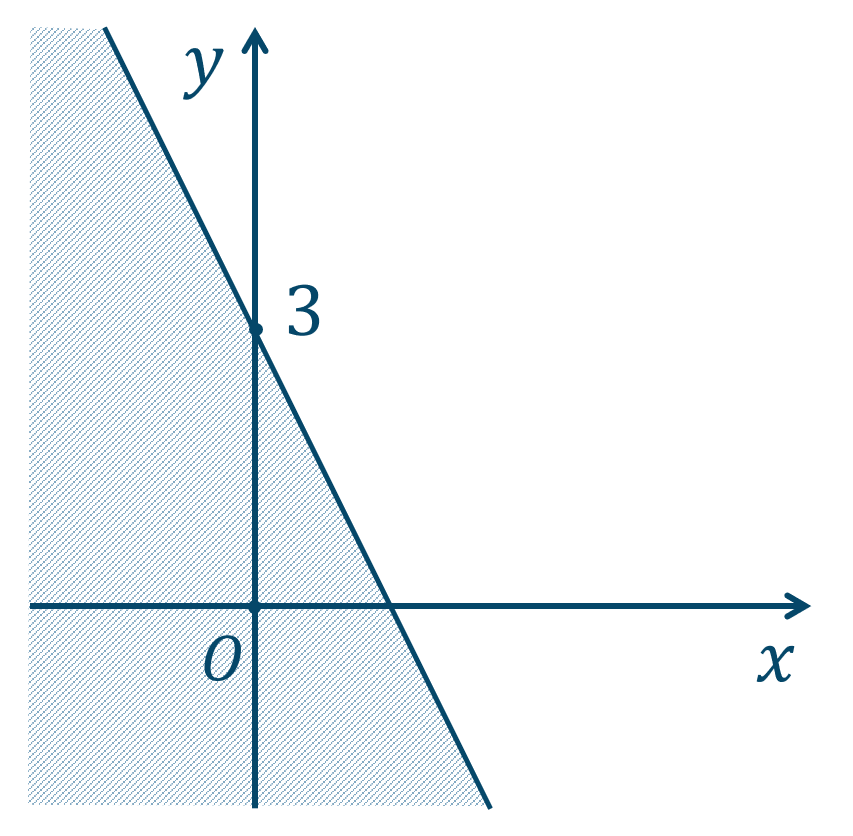
${\small (2)}~$下の図の斜線部分となり、境界線を含まない。

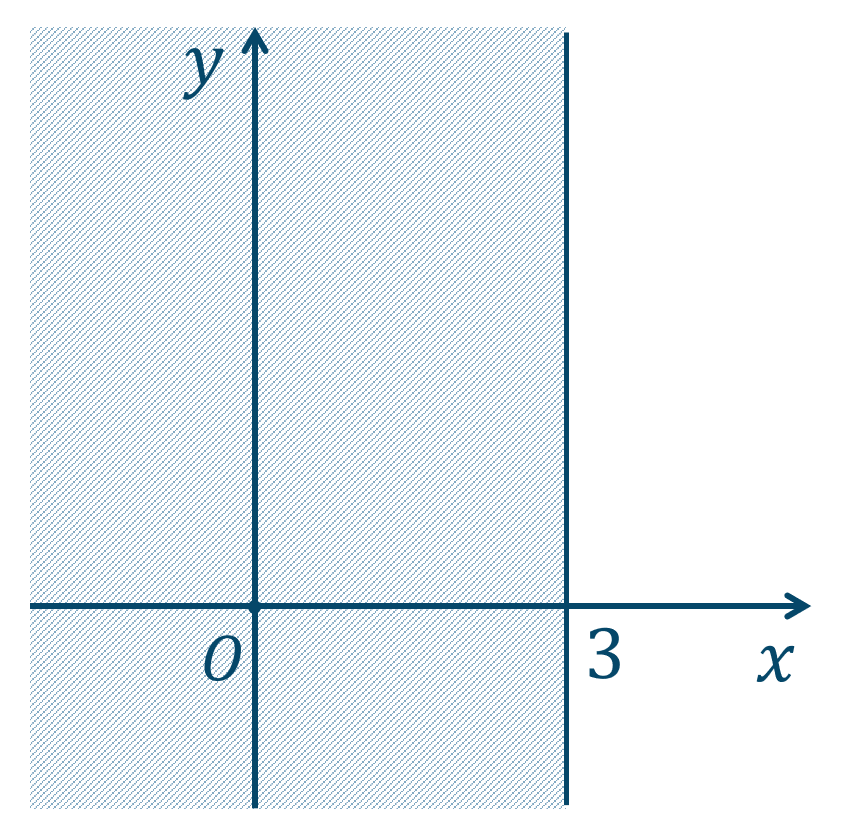
${\small (3)}~$下の図の斜線部分となり、境界線を含む。

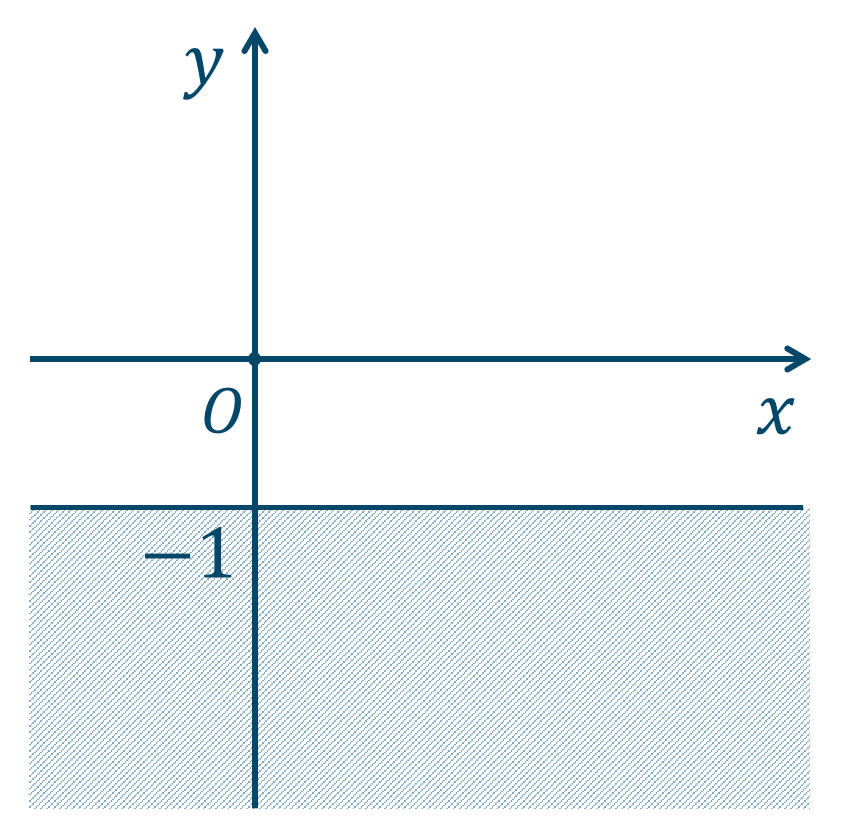
${\small (4)}~$下の図の斜線部分となり、境界線を含む。

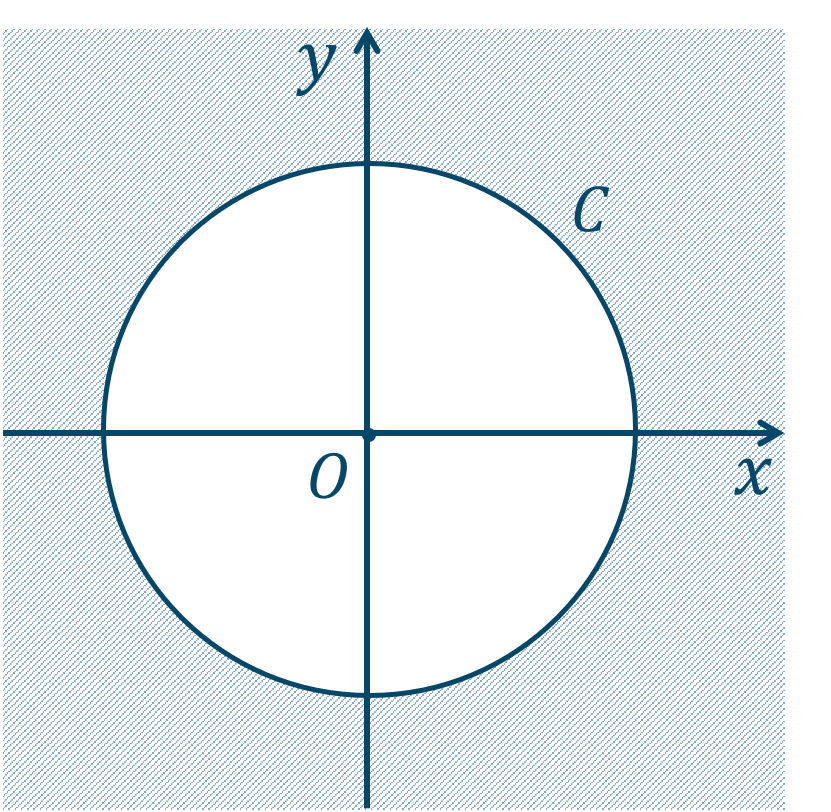
${\small (5)}~$下の図の斜線部分となり、境界線を含まない。

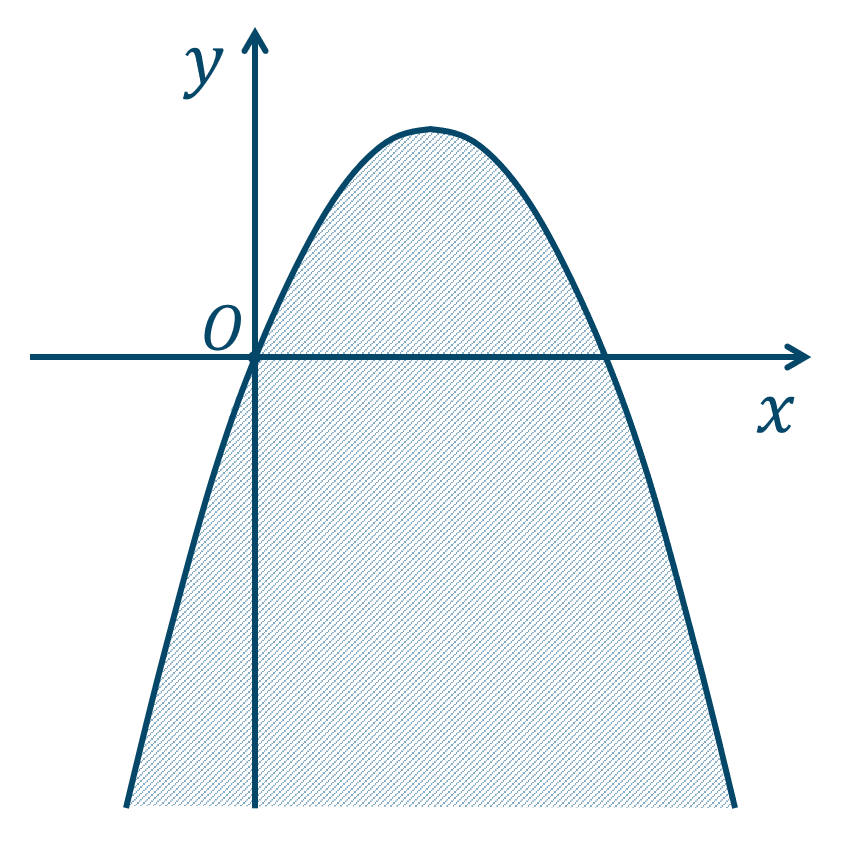
詳しい解説ページはこちらから↓

不等式の表す領域

不等式を満たす点全体の集合を不等式の表す領域といいます。この不等式の表す領域がどのようになるか見ていきましょう。

連立不等式の表す領域①

問題次の不等式の表す領域を求めよ。$${\small (1)}~\biggl\{ \begin{eqnarray} ~x-y+1≧0 \\ ~3x+y+3≧0 \end{eqnarray}$$$${\small (2)}~\biggl\{ \begin{eqnarray} ~y>-\frac{1}{2}x+1 \\ ~(x-2)^2+(y-1)^2>4 \end{eqnarray}$$

[ 解答を見る ]

【解答】
${\small (1)}~$下の図の斜線部分となり、境界線を含む。

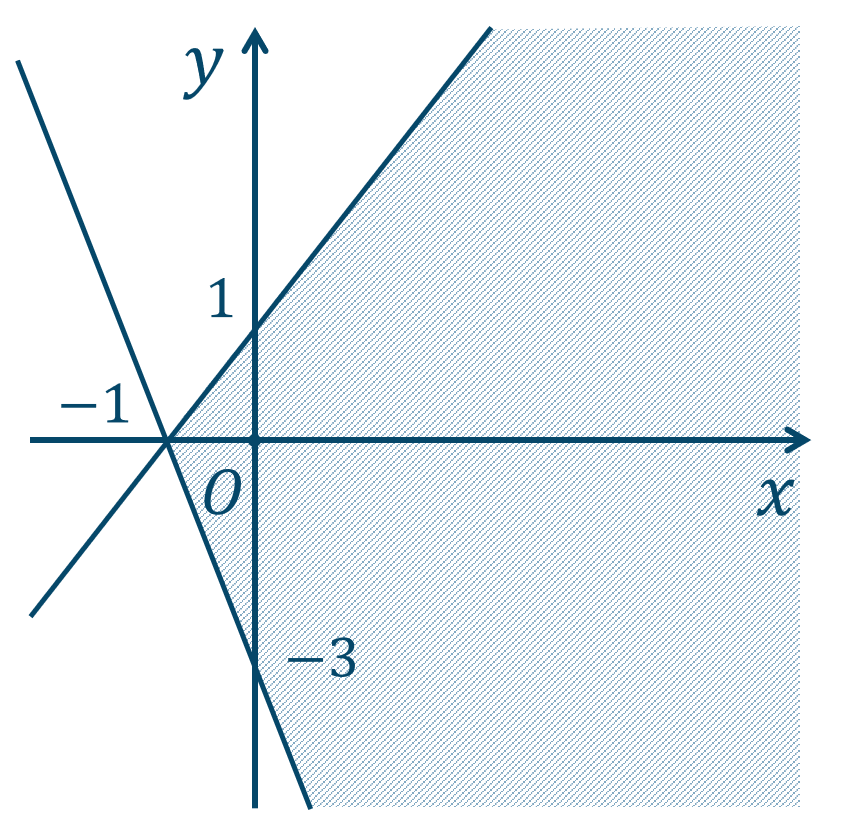
${\small (2)}~$下の図の斜線部分となり、境界線を含まない。

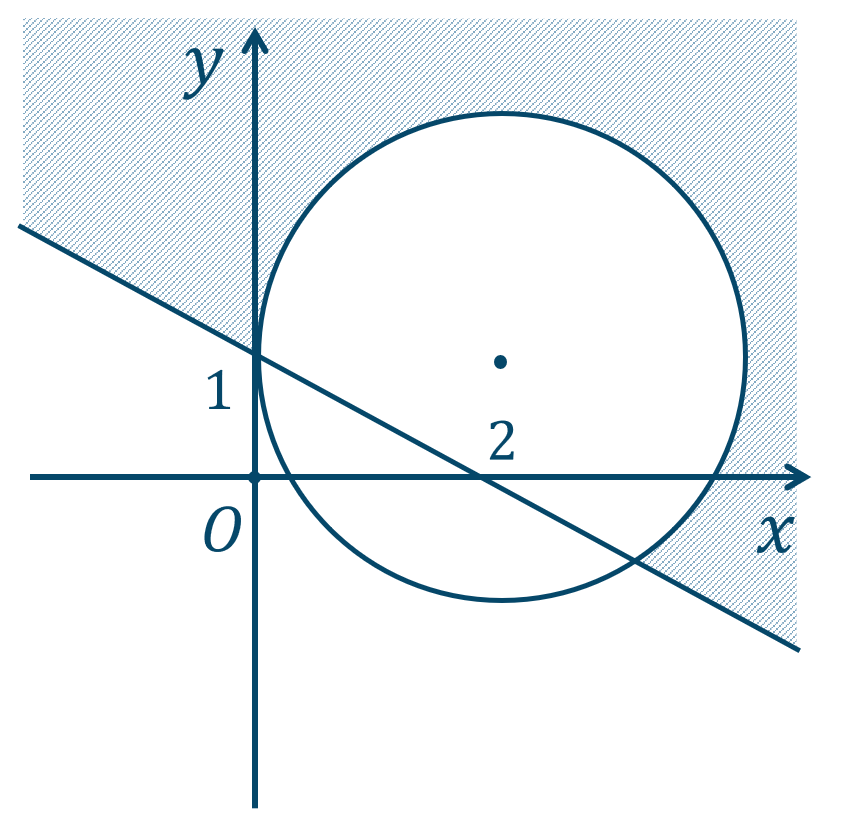
詳しい解説ページはこちらから↓

連立不等式の表す領域①

今回は連立不等式の表す領域の基本について解説していきます。それぞれの不等式の表す領域を求めて共通部分を答えましょう。

連立不等式の表す領域②（積の形）

問題次の不等式が表す領域を求めよ。$${\small (1)}~(2x-1)(x+2y-4)<0$$$${\small (2)}~(x^2+y^2-1)(x+y)>0$$

[ 解答を見る ]

【解答】
${\small (1)}~$下の図の斜線部分となり、境界線を含まない。

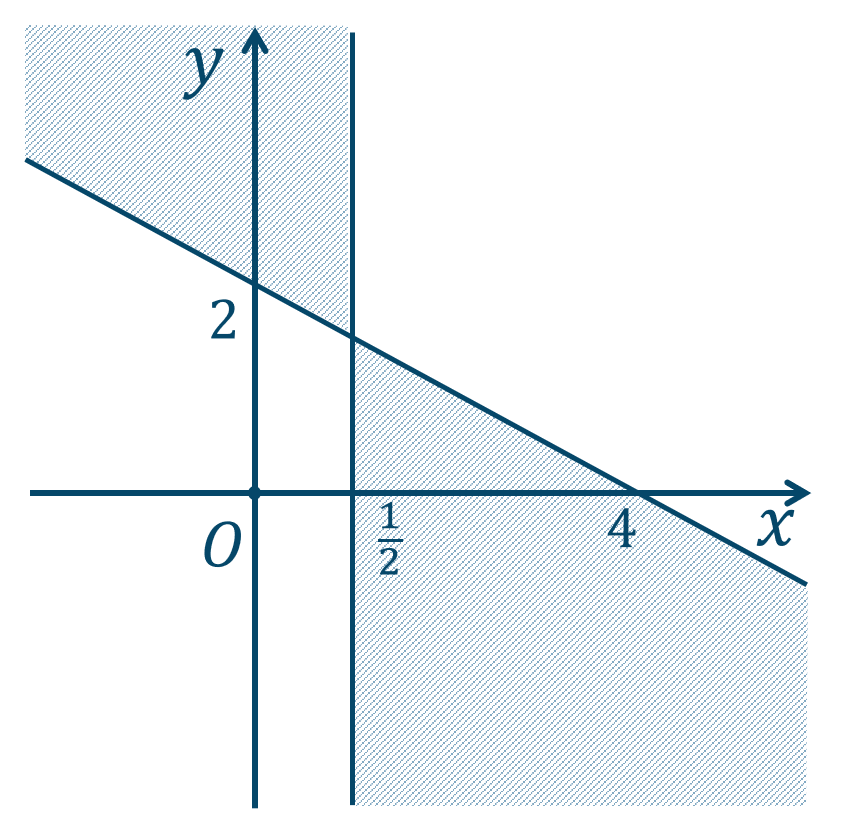
${\small (2)}~$下の図の斜線部分となり、境界線を含まない。

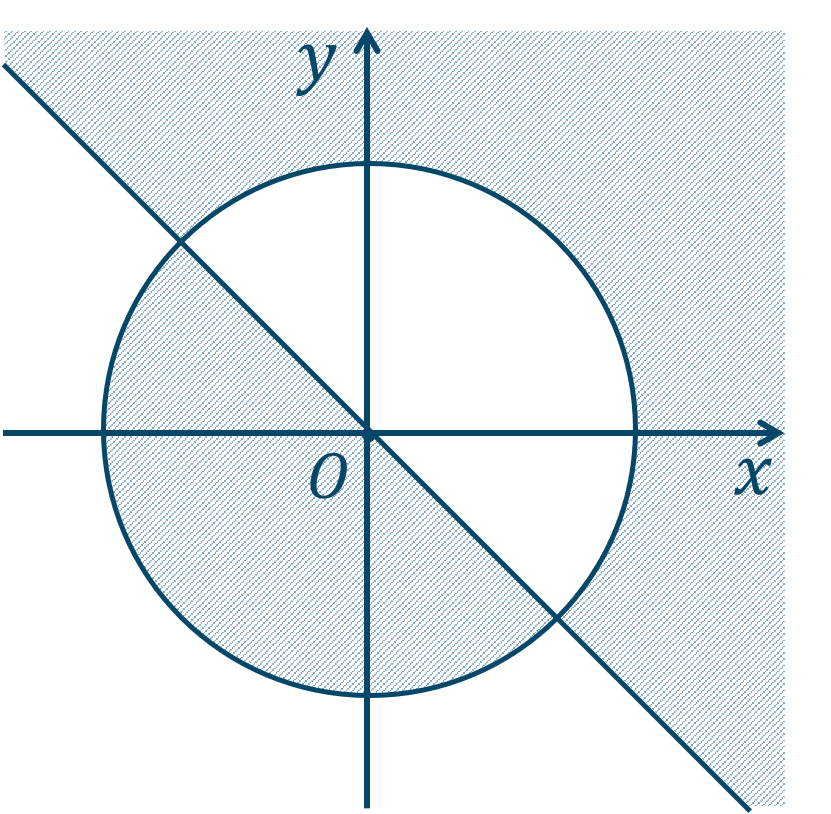
詳しい解説ページはこちらから↓

連立不等式の表す領域②（積の形）

積の形となっている連立不等式の表す領域の求め方について解説していきます。解法のパターンを覚えておきましょう。

線形計画法

問題$x,y$ が以下の領域を満たすとき、$x+y$ の最大値と最小値を求めよ。$$~~~2x+3y-15≦0~,~4x+3y-21≦0$$$$~~~x≧0~,~y≧0$$

[ 解答を見る ]

【解答】
　 $x=3~,~y=3$ のとき最大値 $6$
　 $x=0~,~y=0$ のとき最小値 $0$

詳しい解説ページはこちらから↓

線形計画法

領域と最大値・最小値についての問題を解説していきます。線形計画法という解法の手順を覚えておきましょう。

領域を用いた証明

問題$x^2+y^2<2$ ならば $x^2+y^2-4y-12<0$ であることを証明せよ。

[ 解答を見る ]

【解答】
[証明]$$~P~:~x^2+y^2<2$$$$~Q~:~x^2+y^2-4y-12<0$$とすると、
$P$ は、$x^2+y^2=2$ の内部となります。
$Q$ について式変形すると、$$\hspace{ 10 pt}x^2+y^2-4y-12<0$$$y$ について平方完成すると、$$\hspace{ 10 pt}x^2+(y^2-4y+4-4)-12<0$$$$\hspace{ 50 pt}x^2+(y-2)^2-16<0$$$$\hspace{ 72 pt}x^2+(y-2)^2<16$$よって、$Q$ は円 $x^2+(y-2)^2=16$ の内部となります。

よって、$P~,~Q$ の表す領域を図示すると、

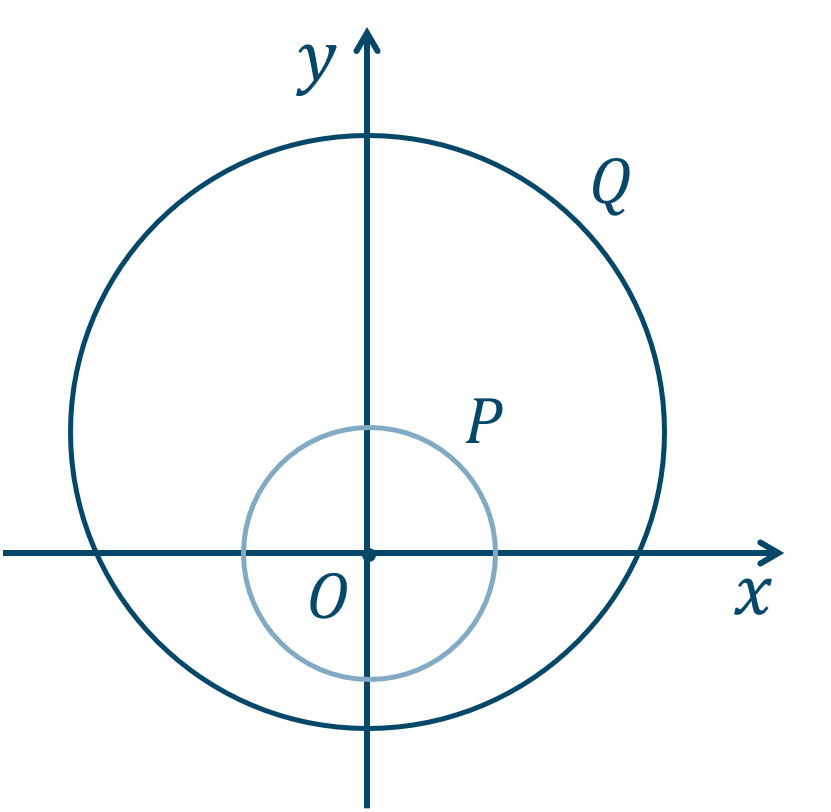
これより、$P\subset Q$ となるので、
$x^2+y^2<2$ ならば $x^2+y^2-4y-12<0$
が成り立ちます。[終]