【問題一覧】数学Ｂ：平面ベクトル

このページは「高校数学Ｂ：平面ベクトル」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。

教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします！

【問題一覧】数学Ｂ：平面ベクトル

【問題一覧】数学Ｂ：平面ベクトル

ベクトルの基本

問題正六角形 ${\rm ABCDEF}$ と対角線の交点 ${\rm O}$ について、次のベクトルをすべて答えよ。
${\small (1)}$ $\overrightarrow{\rm AB}$ と大きさが等しく始点が ${\rm O}$ のベクトル。
${\small (2)}$ $\overrightarrow{\rm AB}$ と向きが同じベクトル。
${\small (3)}$ $\overrightarrow{\rm AB}$ と等しいベクトル。
${\small (4)}$ $\overrightarrow{\rm AB}$ と逆ベクトルの関係のベクトル。

[ 解答を見る ]

【解答】$${\small (1)}~\overrightarrow{\rm OA}~,~ \overrightarrow{\rm OB}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm OD}~,~ \overrightarrow{\rm OE}~,~ \overrightarrow{\rm OF}$$$${\small (2)}~\overrightarrow{\rm FO}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm FC}~,~\overrightarrow{\rm ED}$$$${\small (3)}~\overrightarrow{\rm FO}~,~ \overrightarrow{\rm OC}~,~ \overrightarrow{\rm ED}$$$${\small (4)}~\overrightarrow{\rm BA}~,~ \overrightarrow{\rm CO}~,~ \overrightarrow{\rm OF}~,~\overrightarrow{\rm DE}$$

詳しい解説ページはこちらから↓

ベクトルの基本

今回はベクトルの基本について解説していきます。等しいベクトルになるための条件と逆ベクトルについておさえておきましょう。

ベクトルの実数倍・加法・減法

問題次のベクトル $\overrightarrow{a}~,~\overrightarrow{b}$ について、以下のベクトルを図示せよ。

$${\small (1)}~2\overrightarrow{a}$$$${\small (2)}~-3\overrightarrow{b}$$$${\small (3)}~\overrightarrow{a}+\overrightarrow{b}$$$${\small (4)}~\overrightarrow{a}-\overrightarrow{b}$$

[ 解答を見る ]

詳しい解説ページはこちらから↓

ベクトルの実数倍・加法・減法

今回はベクトルの実数倍・加法・減法について解説していきます。ベクトルの実数倍や加法、減法についての図示の方法をおさえておきましょう。

ベクトルの等式証明

問題４点 ${\rm A~,~B~,~C~,~D}$ について、次の等式を証明せよ。$${\small (1)}~\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CD}=\overrightarrow{\rm AD}$$$${\small (2)}~\overrightarrow{\rm AB}-\overrightarrow{\rm AD}-\overrightarrow{\rm CB}+\overrightarrow{\rm CD}=\overrightarrow{0}$$

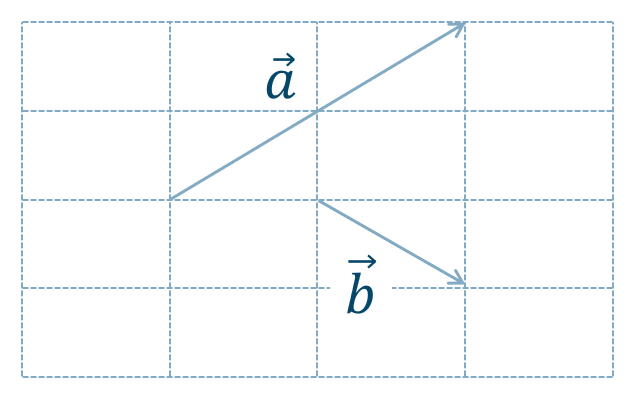
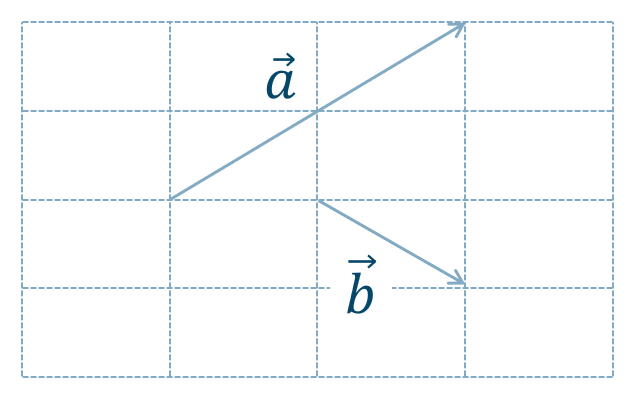
[ 解答を見る ]

詳しい解説ページはこちらから↓

ベクトルの等式証明

今回はベクトルの等式証明について解説していきます。逆ベクトルやベクトルの加法などの性質を利用して証明していきましょう。

ベクトルの演算

問題次の式を簡単にせよ。$${\small (1)}~( 2\overrightarrow{a}-\overrightarrow{b} ) +( 3\overrightarrow{a}+5\overrightarrow{b} )$$$${\small (2)}~( 2\overrightarrow{a}-\overrightarrow{b} )-( 3\overrightarrow{a}+5\overrightarrow{b} )$$$${\small (3)}~2( \overrightarrow{a}-3\overrightarrow{b} )-( \overrightarrow{a}+\overrightarrow{b} )$$$${\small (4)}~3( \overrightarrow{b}-\overrightarrow{c} )+2( \overrightarrow{a}-5\overrightarrow{b} )$$

[ 解答を見る ]

【解答】$${\small (1)}~5\overrightarrow{a}+4\overrightarrow{b}$$$${\small (2)}~-\overrightarrow{a}-6\overrightarrow{b}$$$${\small (3)}~\overrightarrow{a}-7\overrightarrow{b}$$$${\small (4)}~2\overrightarrow{a}-7\overrightarrow{b}-3\overrightarrow{c}$$

詳しい解説ページはこちらから↓

ベクトルの演算

今回はベクトルの演算について解説していきます。計算方法は文字式の計算と同じになるので練習しておきましょう。

ベクトルの分解（正六角形のベクトル）

問題次の正六角形 ${\rm ABCDEF}$ と対角線の交点 ${\rm O}$ について、$\overrightarrow{\rm AB}=\overrightarrow{x}$ $,$ $\overrightarrow{\rm AF}=\overrightarrow{y}$ とするとき、次のベクトルを $\overrightarrow{ x}~,~\overrightarrow{y}$ で表せ。$${\small (1)}~\overrightarrow{\rm OC}$$$${\small (2)}~\overrightarrow{\rm OB}$$$${\small (3)}~\overrightarrow{\rm AO}$$$${\small (4)}~\overrightarrow{\rm BF}$$$${\small (5)}~\overrightarrow{\rm BE}$$$${\small (6)}~\overrightarrow{\rm BD}$$

[ 解答を見る ]

【解答】$${\small (1)}~\overrightarrow{\rm OC}=\overrightarrow{x}$$$${\small (2)}~\overrightarrow{\rm OB}=-\overrightarrow{y}$$$${\small (3)}~\overrightarrow{\rm AO}=\overrightarrow{x}+\overrightarrow{y}$$$${\small (4)}~\overrightarrow{\rm BF}=\overrightarrow{y}-\overrightarrow{x}$$$${\small (5)}~\overrightarrow{\rm BE}=2\overrightarrow{y}$$$${\small (6)}~\overrightarrow{\rm BD}=\overrightarrow{x}+2\overrightarrow{y}$$

詳しい解説ページはこちらから↓

ベクトルの分解（正六角形のベクトル）

今回はベクトルの分解と正六角形のベクトルについて解説していきます。どんなベクトルでも２つのベクトルで表すことができるので、その方法をおさえておきましょう。

ベクトルの成分と大きさ

問題次の $\overrightarrow{a}$ $,$ $\overrightarrow{b}$ $,$ $\overrightarrow{c}$ について、以下の問いに答えよ。$$~~~~~~\overrightarrow{a}=(1~,~3)~,~\overrightarrow{b}=(-2~,~1)$$$$~~~~~~\overrightarrow{c}=(3~,~-5)$$${\small (1)}$ $\overrightarrow{a}$ の大きさを求めよ。
${\small (2)}$ $\overrightarrow{c}$ の大きさを求めよ。
${\small (3)}$ $\overrightarrow{a}+\overrightarrow{b}$ を成分で表し、大きさを求めよ。
${\small (4)}$ $2\overrightarrow{b}-\overrightarrow{c}$ を成分で表し、大きさを求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\sqrt{10}$$$${\small (2)}~\sqrt{34}$$$${\small (3)}~\overrightarrow{a}+\overrightarrow{b}=(-1~,~4)$$$$~~~|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{17}$$$${\small (4)}~2\overrightarrow{b}-\overrightarrow{c}=(-7~,~7)$$$$~~~|2\overrightarrow{b}-\overrightarrow{c}|=7\sqrt{2}$$

詳しい解説ページはこちらから↓

ベクトルの成分と大きさ

ベクトルの成分と大きさについて解説していきます。成分の計算方法と大きさの求め方をしっかりと覚えておきましょう。

ベクトルの成分と式変形

問題次の $\overrightarrow{a}$ $,$ $\overrightarrow{b}$ $,$ $\overrightarrow{c}$ について、以下の問いに答えよ。$$~~~~~~\overrightarrow{a}=(1~,~3)~,~\overrightarrow{b}=(-2~,~1)$$$$~~~~~~\overrightarrow{c}=(3~,~-5)$$${\small (1)}$ $\overrightarrow{a} +2\overrightarrow{d}=3\overrightarrow{b}-\overrightarrow{c}$ を満たす $\overrightarrow{d}$ の成分を求めよ。
${\small (2)}$ $\overrightarrow{c}$ を $\overrightarrow{c}=m\overrightarrow{a}+n\overrightarrow{b}$ の形で表せ。

[ 解答を見る ]

【解答】$${\small (1)}~\overrightarrow{d}=\left( -5~,~\frac{5}{2} \right)$$$${\small (2)}~\overrightarrow{c}=-\overrightarrow{a}-2\overrightarrow{b}$$

詳しい解説ページはこちらから↓

ベクトルの成分と式変形

今回はベクトル成分と式変形について解説していきます。ベクトルの相等とベクトルの分解を利用して解いていきましょう。

ベクトルの成分と平行条件

問題次の問いに答えよ。
${\small (1)}$ $\overrightarrow{a}=(1~,~3)$ と平行な単位ベクトル $\overrightarrow{e}$ を成分で表せ。
${\small (2)}$ ２つのベクトル $\overrightarrow{b}=(x~,~2)$ と $\overrightarrow{c}=(-1~,~x-3)$ が平行になるとき、$x$ の値を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\overrightarrow{e}=\left( \frac{1}{\sqrt{10}}~,~\frac{3}{\sqrt{10}}\right)$$$$\hspace{ 32 pt}\left( -\frac{1}{\sqrt{10}}~,~-\frac{3}{\sqrt{10}}\right)$$$${\small (2)}~x=1~,~2$$

詳しい解説ページはこちらから↓

ベクトルの成分と平行条件

今回はベクトルの成分と平行条件について解説していきます。２つのベクトルが平行のとき、向きが等しくなることから実数倍のベクトルの条件を使いましょう。

点の座標とベクトルの成分

問題４点 ${\rm O}(0~,~0)$ $,$ ${\rm A}(3~,~4)$ $,$ ${\rm B}(2~,~-1)$ $,$ ${\rm C}(-3~,~2)$ について、次のベクトルを成分で表し、その大きさを求めよ。$${\small (1)}~\overrightarrow{\rm OA}$$$${\small (2)}~\overrightarrow{\rm OB}$$$${\small (3)}~\overrightarrow{\rm AC}$$$${\small (4)}~\overrightarrow{\rm BC}$$

[ 解答を見る ]

【解答】$${\small (1)}~\overrightarrow{\rm OA}=(3~,~4)$$$$~~~|\overrightarrow{\rm OA}|=5$$$${\small (2)}~\overrightarrow{\rm OB}=(2~,~-1)$$$$~~~|\overrightarrow{\rm OB}|=\sqrt{5}$$$${\small (3)}~\overrightarrow{\rm AC}=(-6~,~-2)$$$$~~~|\overrightarrow{\rm AC}|=2\sqrt{10}$$$${\small (4)}~\overrightarrow{\rm BC}=(-5~,~3)$$$$~~~|\overrightarrow{\rm BC}|=\sqrt{34}$$

詳しい解説ページはこちらから↓

点の座標とベクトルの成分

回は平面上に与えらた点の座標とベクトルの成分について解説していきます。点の座標からベクトルの成分の求め方を覚えておきましょう。

平行四辺形とベクトル

問題平面上の４点 ${\rm A}(3~,~4)$ $,$ ${\rm B}(2~,~-1)$ $,$ ${\rm C}(-3~,~2)$ $,$ ${\rm D}(x~,~y)$ について、この４点が平行四辺形をつくるときの点 ${\rm D}$ の座標を求めよ。

[ 解答を見る ]

【解答】$$~~~(-2~,~7)~,~(-4~,~-3)~,~(8~,~1)$$

詳しい解説ページはこちらから↓

平行四辺形とベクトル

平行四辺形のベクトルについて解説していきます。与えられた４点が平行四辺形を作るときの条件を考えましょう。

ベクトルの内積①（基本）

問題次の問いに答えよ。
${\small (1)}$ $|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4$ として、$\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角が $\theta$ が以下の値のとき、内積 $\overrightarrow{a}\cdot\overrightarrow{b}$ を求めよ。$$~{\large ①}~\theta=30^\circ~~~~~~~~{\large ②}~\theta=60^\circ$$$$~{\large ③}~\theta=90^\circ~~~~~~~~{\large ④}~\theta=135^\circ$$${\small (2)}$ １辺の長さが $3$ の正三角形 ${\rm ABC}$ と辺 ${\rm BC}$ の中点 ${\rm M}$ について、次の内積を求めよ。$$~{\large ①}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}~~~~~~~~{\large ②}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AM}$$$$~{\large ③}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BC}~~~~~~~~{\large ④}~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm BC}$$

[ 解答を見る ]

【解答】$${\small (1)}$$$$~{\large ①}~6\sqrt{3}$$$$~{\large ②}~6$$$$~{\large ③}~0$$$$~{\large ④}~-6\sqrt{2}$$$${\small (2)}$$$$~{\large ①}~\frac{9}{2}$$$$~{\large ②}~\frac{27}{4}$$$$~{\large ③}~-\frac{9}{2}$$$$~{\large ④}~\frac{9}{2}$$

詳しい解説ページはこちらから↓

ベクトルの内積①（基本）

今回はベクトルの内積について解説していきます。公式を覚えるのはもちろんなのですが、始点を揃えてなす角を考える点もおさえておきましょう。

ベクトルの内積②（成分利用）

問題次の $\overrightarrow{a}$ $,$ $\overrightarrow{b}$ $,$ $\overrightarrow{c}$ について、以下の内積に答えよ。$$~~~~~~\overrightarrow{a}=(1~,~3)~,~\overrightarrow{b}=(-2~,~1)$$$$~~~~~~\overrightarrow{c}=(3~,~-5)$$$${\small (1)}~\overrightarrow{a}\cdot\overrightarrow{b}$$$${\small (2)}~\overrightarrow{b}\cdot\overrightarrow{c}$$$${\small (3)}~\overrightarrow{a}\cdot\overrightarrow{c}$$

[ 解答を見る ]

【解答】$${\small (1)}~1$$$${\small (2)}~-11$$$${\small (3)}~-12$$

詳しい解説ページはこちらから↓

ベクトルの内積②（成分利用）

ベクトルの内積について解説していきます。今回は成分を用いたベクトルの内積になります。計算方法を覚えておきましょう。

ベクトルのなす角

問題次の２つのベクトルのなす角を求めよ。$${\small (1)}~\overrightarrow{a}=(2~,~2\sqrt{3})~,~\overrightarrow{b}=(-\sqrt{3}~,~3)$$$${\small (2)}~\overrightarrow{a}=(-3~,~1)~,~\overrightarrow{b}=(1~,~-2)$$

[ 解答を見る ]

【解答】$${\small (1)}~60^\circ$$$${\small (2)}~135^\circ$$

詳しい解説ページはこちらから↓

ベクトルのなす角

今回は２つのベクトルのなす角について解説していきます。内積の２通りの求め方からなす角を求めましょう。

ベクトルの垂直条件

問題次の問いに答えよ。
${\small (1)}$ $\overrightarrow{a}=(1~,~3)$ に垂直な単位ベクトルを成分で表せ。
${\small (2)}$ $\overrightarrow{b}=(2~,~-1)$ に垂直で大きさが $\sqrt{5}$ のベクトルの成分で表せ。

[ 解答を見る ]

【解答】$${\small (1)}~\left(-\frac{3}{\sqrt{10}}~,~\frac{1}{\sqrt{10}}\right)~,~\left(\frac{3}{\sqrt{10}}~,~-\frac{1}{\sqrt{10}}\right)$$$${\small (2)}~(1~,~2)~,~(-1~,~-2)$$

詳しい解説ページはこちらから↓

ベクトルの垂直条件

今回はベクトルの垂直条件について解説していきます。２つのベクトルが垂直であるとき、なす角が 90° となるので内積が 0 となることを条件式としましょう。

内積の性質を用いた等式証明

問題次の等式を証明せよ。$${\small (1)}~(\overrightarrow{a}-2\overrightarrow{b})\cdot(\overrightarrow{c}+3\overrightarrow{d})$$$$\hspace{ 6 pt}=\overrightarrow{a}\cdot\overrightarrow{c}+3\overrightarrow{a}\cdot\overrightarrow{d}-2\overrightarrow{b}\cdot\overrightarrow{c}-6\overrightarrow{b}\cdot\overrightarrow{d}$$$${\small (2)}~|3\overrightarrow{a}-2\overrightarrow{b}|^2$$$$\hspace{ 6 pt}=9|\overrightarrow{a}|^2-12\overrightarrow{a}\cdot\overrightarrow{b}+4|\overrightarrow{b}|^2$$

[ 解答を見る ]

詳しい解説ページはこちらから↓

内積を用いた等式証明

今回はベクトルの内積の性質を用いた等式証明について解説していきます。内積の性質である分配法則には注意して計算していきましょう。

内積の性質の利用（ベクトルの大きさと内積）

問題次の問いに答えよ。
${\small (1)}$ $|\overrightarrow{a}|=2~,~|\overrightarrow{b}|=1$ で $\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角が $120^\circ$ のとき、ベクトル $2\overrightarrow{a}-\overrightarrow{b}$ の大きさを求めよ。
${\small (2)}$ $|\overrightarrow{a}|=\sqrt{3}~,~|\overrightarrow{b}|=1~,~|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{7}$ のとき、$\overrightarrow{a}$ と $\overrightarrow{b}$ のなす角を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\sqrt{21}$$$${\small (2)}~30^\circ$$

詳しい解説ページはこちらから↓

内積の性質の利用（ベクトルの大きさと内積）

今回はベクトルの内積の性質を利用した問題について解説していきます。与えられた式を２乗して計算していきましょう。

内分点・外分点の位置ベクトル

問題点 ${\rm A~,~B}$ の位置ベクトルをそれぞれ $\overrightarrow{a}~,~\overrightarrow{b}$ とするとき、次の位置ベクトルを求めよ。
${\small (1)}$ 線分 ${\rm AB}$ の中点
${\small (2)}$ 線分 ${\rm AB}$ を $2:1$ に内分する点
${\small (3)}$ 線分 ${\rm AB}$ を $3:2$ に外分する点

[ 解答を見る ]

【解答】$${\small (1)}~\frac{1}{2}\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$$$${\small (2)}~\frac{1}{3}\overrightarrow{a}+\frac{2}{3}\overrightarrow{b}$$$${\small (3)}~-2\overrightarrow{a}+3\overrightarrow{b}$$

詳しい解説ページはこちらから↓

内分点・外分点の位置ベクトル

今回は内分点・外分点の位置ベクトルについて解説していきます。座標上の点の位置をベクトルで表す方法を覚えておきましょう。

重心の位置ベクトル

問題$\triangle {\rm ABC}$ の重心を ${\rm G}$ とするとき、次の等式が成り立つことを証明せよ。$$~~~\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}$$

[ 解答を見る ]

詳しい解説ページはこちらから↓

重心の位置ベクトル

三角形の重心の位置ベクトルについて解説していきます。今回は三角形の重心の位置ベクトルの公式を用いて等式を証明していきましょう。

３点が同一直線上にある条件

問題平行四辺形 ${\rm ABCD}$ において、辺 ${\rm AB}$ を $2:1$ に内分する点を ${\rm P}$ 、対角線 ${\rm BD}$ を $1:3$ に内分する点を ${\rm Q}$ とするとき、３点 ${\rm P~,~Q~,~C}$ は同一直線上にあることを示せ。

[ 解答を見る ]

詳しい解説ページはこちらから↓

３点が同一直線上にある条件

今回は３点が同一直線上にある条件について解説していきます。同一直線上にある条件式が成り立つことを示すように式変形していきましょう。

２直線の交点のベクトル

問題$\triangle {\rm OAB}$ について、線分 ${\rm OA}$ を $2:3$ に内分する点を ${\rm D}$ 、線分 ${\rm OB}$ を $2:1$ に内分する点を ${\rm E}$ 、直線 ${\rm AE}$ と ${\rm BD}$ との交点を ${\rm F}$ とする。$\overrightarrow{\rm OA}=\overrightarrow{a}$ $,$ $\overrightarrow{\rm OB}=\overrightarrow{b}$ とするとき、$\overrightarrow{\rm OF}$ を $\overrightarrow{a}~,~\overrightarrow{b}$ を用いて表せ。

[ 解答を見る ]

【解答】$$~~~\overrightarrow{\rm OF}=\frac{2}{11}\overrightarrow{a}+\frac{6}{11}\overrightarrow{b}$$

詳しい解説ページはこちらから↓

２直線の交点とベクトル

今回は三角形の内部にある２直線の交点の位置ベクトルについて解説していきます。２つの三角形に分けてそれぞれについて位置ベクトルを求める方法を覚えておきましょう。

ベクトルと三角形の面積

問題次の問いに答えよ。
${\small (1)}$ ３点 ${\rm O~,~A~,~B}$ について、$|\overrightarrow{\rm OA}|=4$ $,$ $|\overrightarrow{\rm OB}|=\sqrt{5}$ $,$ $\overrightarrow{\rm OA}\cdot\overrightarrow{\rm OB}=2\sqrt{5}$ のとき、 $\triangle {\rm OAB}$ の面積を求めよ。
${\small (2)}$ ３点 ${\rm O}=(0~,~0)$ $,$ ${\rm A}=(3~,~4)$ $,$ ${\rm B}=(2~,~-1)$ を頂点とする $\triangle {\rm OAB}$ の面積を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\sqrt{15}$$$${\small (2)}~\frac{11}{2}$$

詳しい解説ページはこちらから↓

ベクトルと三角形の面積

ベクトルと三角形の面積について解説していきます。大きさと内積が条件の公式とベクトルの成分が条件の公式をそれぞれ覚えておきましょう。

直線のベクトル方程式

問題次の問いに答えよ。
${\small (1)}$ 点 ${\rm A}(3~,~4)$ を通り、$\overrightarrow{d}=(2~,~-1)$ が方向ベクトルである直線の方程式を媒介変数表示で表せ。また、媒介変数を消去した式で表せ。
${\small (2)}$ ２点 ${\rm A}(1~,~3)~,~{\rm B}(-2~,~1)$ を通る直線の媒介変数表示で表せ。また、媒介変数を消去した式で表せ。

[ 解答を見る ]

【解答】$${\small (1)}~\biggl\{~ \begin{eqnarray} x=3+2t \\ y=4-t\end{eqnarray}$$$$~~~x+2y-11=0$$$${\small (2)}~\biggl\{~ \begin{eqnarray} x=1-3t \\ y=3-2t \end{eqnarray}$$$$~~~2x-3y+7=0$$

詳しい解説ページはこちらから↓

直線のベクトル方程式

今回は直線のベクトル方程式について解説していきます。２通りの式の立て方と媒介変数表示についておさえておきましょう。

ベクトルと点の存在範囲

問題$\triangle {\rm OAB}$ に対して、$\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}$ とする実数 $s~,~t$ が次の条件を満たすとき、点 ${\rm P}$ の存在範囲を求めよ。$${\small (1)}~s+t=2~,~s≧0~,~t≧0$$$${\small (2)}~s+t≦\frac{1}{2}~,~s≧0~,~t≧0$$

[ 解答を見る ]

詳しい解説ページはこちらから↓

ベクトルと点の存在範囲

ベクトルと点の存在範囲について解説していきます。ベクトルの分解の式から任意の点の位置ベクトルの場所を特定しましょう。

法線ベクトル

問題次の問いに答えよ。
${\small (1)}$ 点 ${\rm A}(1~,~3)$ を通り、$\overrightarrow{n}=(-2~,~1)$ が法線ベクトルである直線の方程式を求めよ。
${\small (2)}$ 次の２直線のなす角 $\theta$ を求めよ。ただし、$0^\circ≦\theta≦90^\circ$ とする。
$~~~~3x+2y-1=0~,~5x-y+7=0$

[ 解答を見る ]

【解答】$${\small (1)}~2x-y+1=0$$$${\small (2)}~45^\circ$$

詳しい解説ページはこちらから↓

法線ベクトル

今回は法線ベクトルについて解説していきます。法線ベクトルの基本と法線ベクトルを利用した２直線のなす角の求め方をおさえておきましょう。

円のベクトル方程式

問題平面上の定点 ${\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})$ と任意の点 ${\rm P}(\overrightarrow{p})$ に対して、次のベクトルはどんな図形を示すか答えよ。$${\small (1)}~|\overrightarrow{p}-\overrightarrow{a}|=3$$$${\small (2)}~|\overrightarrow{p}-\overrightarrow{a}|=|\overrightarrow{a}-\overrightarrow{b}|$$$${\small (3)}~|2\overrightarrow{p}-\overrightarrow{b}|=6$$

[ 解答を見る ]

詳しい解説ページはこちらから↓