【問題一覧】数学Ａ：場合の数と確率

このページは「高校数学Ａ：場合の数と確率」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。

教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします！

【問題一覧】数学Ａ：場合の数と確率

【問題一覧】数学Ａ：場合の数と確率

集合の要素の個数

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、次の値を求めよ。$${\small (1)}~n({\rm A})$$$${\small (2)}~n({\rm B})$$$${\small (3)}~n({\rm A} \cap {\rm B})$$$${\small (4)}~n({\rm A} \cup {\rm B})$$

[ 解答を見る ]

【解答】$${\small (1)}~n({\rm A})=50$$$${\small (2)}~n({\rm B})=33$$$${\small (3)}~n({\rm A} \cap {\rm B})=16$$$${\small (4)}~n({\rm A} \cup {\rm B})=67$$

詳しい解説ページはこちらから↓

集合の要素の個数

今回は集合において、その集合に属する要素の個数の表し方を解説していきます。また、倍数の数え方もしっかり覚えておきましょう。

補集合の要素の個数

問題あるクラスの生徒 $40$ 人に数学と英語の好き・嫌いのアンケートを行った。数学が好きな生徒は $21$ 人、英語が好きな生徒は $17$ 人、どちらも好きな生徒は $8$ 人いた。このとき、次の生徒の人数を答えよ。
${\small (1)}~$数学が嫌いな生徒
${\small (2)}~$数学が嫌いで英語が好きな生徒
${\small (3)}~$数学と英語の少なくとも一方が好きな生徒
${\small (4)}~$数学と英語のどちらも嫌いな生徒

[ 解答を見る ]

【解答】
${\small (1)}~$19人$~~~~~~{\small (2)}~$9人
${\small (3)}~$30人$~~~~~~{\small (4)}~$10人

詳しい解説ページはこちらから↓

補集合の要素の個数

今回は補集合についての要素の個数の求め方を解説していきます。ド・モルガンの法則についてもおさえておきましょう。

３つの集合の要素の個数

問題1～100までの自然数のうち、２の倍数の集合を $\rm A$、３の倍数の集合を $\rm B$ とするとき、５の倍数の集合を $\rm C$ とするとき、次の値を求めよ。$${\small (1)}~n({\rm A} \cap {\rm C})$$$${\small (2)}~n({\rm B} \cup {\rm C})$$$${\small (3)}~n({\rm A} \cap {\rm B} \cap {\rm C})$$$${\small (4)}~n({\rm A} \cup {\rm B} \cup {\rm C})$$

[ 解答を見る ]

【解答】$${\small (1)}~n({\rm A} \cap {\rm C})=10$$$${\small (2)}~n({\rm B} \cup {\rm C})=47$$$${\small (3)}~n({\rm A} \cap {\rm B} \cap {\rm C})=3$$$${\small (4)}~n({\rm A} \cup {\rm B} \cup {\rm C})=74$$

詳しい解説ページはこちらから↓

３つの集合の要素の個数

３つの集合の要素の個数について解説していきます。このときでも基本は同じでベン図を描いて視覚的に解いていきましょう。また、倍数の数え方もおさえておきましょう。

和の法則と積の法則

問題A町からB町までは３つの交通手段があり、B町からC町までは４つの交通手段があり、A町からC町まで直接行く交通手段は２つある。A町からC町まで行く方法は全部で何通りあるか答えよ。

[ 解答を見る ]

【解答】
$~~~$14通り

詳しい解説ページはこちらから↓

和の法則と積の法則

今回は場合の数と確率を計算していくうえで大事になる２つの法則である「和の法則と積の法則」を解説していきます。この２つの法則の違いを理解しておきましょう。

約数の個数と展開式の項の個数

問題次の場合の数を求めよ。
${\small (1)}~$$200$ の正の約数の個数を求めよ。
${\small (2)}~$$360$ の正の約数の個数を求めよ。
${\small (3)}~$$(x+y)(a+b+c)$ を展開すると、項はいくつできるか。

[ 解答を見る ]

【解答】
${\small (1)}~$12個$~~~~~~{\small (2)}~$24個$~~~~~~{\small (3)}~$6個

詳しい解説ページはこちらから↓

約数の個数と展開式の項の数

今回は約数の個数と展開式の項の数の２つの問題パターンを解説していきます。それぞれ求め方を覚えておきましょう。

順列と階乗の記号

問題次の計算をせよ。$${\small (1)}~{}_{5}{\rm P}_{3}$$$${\small (2)}~{}_{6}{\rm P}_{0}$$$${\small (3)}~{}_{4}{\rm P}_{4}$$$${\small (4)}~6!$$$${\small (5)}~0!$$$${\small (6)}~7!\div5!$$

[ 解答を見る ]

【解答】$${\small (1)}~60~~~~~~~~{\small (2)}~1~~~~~~{\small (3)}~24$$$${\small (4)}~720~~~~~~{\small (5)}~1~~~~~~{\small (6)}~42$$

詳しい解説ページはこちらから↓

順列と階乗の記号

今回は順列と階乗の記号とその計算方法について解説していきます。計算方法をしっかりお覚えておきましょう。

文字の順列

問題 $a,b,c,d,e$ を一列に並べるとき、次の場合の数を求めよ。
${\small (1)}~$$a,b$ が隣り合う並べ方
${\small (2)}~$$a,b$ が両端にくる並べ方

[ 解答を見る ]

【解答】
${\small (1)}~$48通り$~~~~~~{\small (2)}~$12通り

詳しい解説ページはこちらから↓

文字の順列

今回は文字を並べる順列の解法についてです。ただ単に並べるだけでなく、条件があるパターンで順列の記号 P を使っても解けないものが多いのでパターン別に解法をおさえておきましょう

数字の順列

問題0 , 1 , 2 , 3 , 4 の５つの数字が１つずつあるとき、次の場合の数を求めよ。
${\small (1)}~$３桁の整数
${\small (2)}~$３桁の暗証番号
${\small (3)}~$３桁の偶数
${\small (4)}~$３桁の整数のうち、300以上の整数

[ 解答を見る ]

【解答】
${\small (1)}~$48通り$~~~~~~{\small (2)}~$60通り
${\small (3)}~$30通り$~~~~~~{\small (4)}~$24通り

詳しい解説ページはこちらから↓

数字の順列

今回は数字を並べるパターンを理解していきましょう。「箱を描いて、それぞれの箱に入れる場合の数を考える」解法を用いて解きましょう。

円順列とじゅず順列

問題８種類の球を用いて次の場合の数を求めよ。
${\small (1)}~$円状に並べる方法
${\small (2)}~$じゅずを作るときの方法

[ 解答を見る ]

【解答】
${\small (1)}~$5040通り$~~~~~~{\small (2)}~$2520通り

詳しい解説ページはこちらから↓

円順列とじゅず順列

円順列とじゅず順列について解説します。円順列では回転したときにダブりが出てくることです。じゅず順列に関しては表裏でのダブりも考慮しましょう。

条件付き円順列

問題先生２人と生徒４人が円形のテーブルに座るとき、次の場合の数を求めよ。
${\small (1)}~$すべての座り方
${\small (2)}~$先生２人が隣り合う座り方
${\small (3)}~$先生２人が向い合う座り方

[ 解答を見る ]

【解答】
${\small (1)}~$120通り$~~~~~~{\small (2)}~$48通り$~~~~~~{\small (3)}~$24通り

詳しい解説ページはこちらから↓

条件付き円順列

今回は様々な条件の付いた円順列を解説していきます。基本的な解法は前回の「特定のものを固定させる！」となります。

重複を許す順列

問題次の場合の数を答えよ。
${\small (1)}~$$ a,b,c,d,e$ の５つの文字から、重複を許して３つの文字を一列に並べる並べ方
${\small (2)}~$0 , 1 , 2 , 3 , 4 の５つの数字から、重複を許して３桁の自然数を作る作り方

[ 解答を見る ]

【解答】
${\small (1)}~$125通り$~~~~~~{\small (2)}~$100通り

詳しい解説ページはこちらから↓

重複を許す順列

今回の順列パターンは重複を許す順列です。今までの順列では一度並べた文字や数字は使えませんでしたが、重複順列では同じ文字や数字を何度でも使えるようになります。

２つのグループに分ける

問題９人を以下の方法で分ける場合の数を求めよ。
${\small (1)}~$A、Bの２部屋に分ける方法（ただし、空室があってもよい）
${\small (2)}~$A、Bの２グループに分ける方法
${\small (3)}~$２つのグループに分ける方法

[ 解答を見る ]

【解答】
${\small (1)}~$512通り$~~~~~~{\small (2)}~$510通り$~~~~~~{\small (3)}~$255通り

詳しい解説ページはこちらから↓

２つのグループに分ける

グループ分けの場合の数で、２つのグループに分ける方法を解説していきましょう。基本的には重複順列の考え方で解けますが、分けるときに条件があると場合の数が変わってきますので注意が必要です。

組合せの記号

問題次の計算をせよ。$${\small (1)}~{}_{5}{\rm C}_{3}$$$${\small (2)}~{}_{7}{\rm C}_{2}$$ $${\small (3)}~{}_{9}{\rm C}_{7}$$$${\small (4)}~{}_{6}{\rm C}_{6}$$$${\small (5)}~{}_{5}{\rm C}_{0}$$

[ 解答を見る ]

【解答】$${\small (1)}~10~~~~~~{\small (2)}~21~~~~~~{\small (3)}~36$$$${\small (4)}~1~~~~~~~~{\small (5)}~1$$

詳しい解説ページはこちらから↓

組合せの記号

今回は組合せの記号とその計算方法の解説をしていきます。順列の記号と混合しやすいのでしっかりと区別ができるようになりましょう。

順列と組合せ

問題 $a,b,c,d,e$ の５つの文字がそれぞれ１つずつあるとき、次の問いに答えよ。
${\small (1)}~$３つの文字を選び一列に並べるときの場合の数
${\small (2)}~$３つの文字を選ぶときの場合の数

[ 解答を見る ]

【解答】
${\small (1)}~$60通り$~~~~~~{\small (2)}~$10通り

詳しい解説ページはこちらから↓

順列と組合せ

今回は順列と組合せについてです。この２つは、それぞれどんなときに使うのかをしっかりと区別し理解して計算できるようになりましょう。

図形と組合せ

問題次の場合の数を求めよ。
${\small (1)}~$５本の平行線と、それとは別の３本の平行線とが交わってできる平行四辺形の数
${\small (2)}~$正八角形について、頂点を結んでできる三角形の個数
${\small (3)}~$正八角形について、頂点を結んでできる対角線の本数

[ 解答を見る ]

【解答】
${\small (1)}~$30個$~~~~~~{\small (2)}~$56個$~~~~~~{\small (3)}~$20本

詳しい解説ページはこちらから↓

図形と組合せ

組合せの計算を使って図形のでき方の場合の数が何通りあるかを計算するパターンを見ていきます。図形の問題のように見えますが、単純な組合せの問題になるので惑わされずにしっかりと問題文を読み取れるように！

代表を選ぶ

問題男子５人、女子４人から代表を３人選ぶ。このとき、次の場合の数を求めよ。
${\small (1)}~$すべての選び方
${\small (2)}~$男子１人、女子２人となる選び方
${\small (3)}~$少なくとも女子１人を選ぶ選び方
${\small (4)}~$男子から３人、または女子から３人を選ぶ選び方

[ 解答を見る ]

【解答】
${\small (1)}~$84通り$~~~~~~{\small (2)}~$30通り
${\small (3)}~$74通り$~~~~~~{\small (4)}~$14通り

詳しい解説ページはこちらから↓

代表を選ぶ

組合せの記号を使って代表を選ぶときの場合の数を解説していきます。組合せの記号を用いると、大量の樹形図を描くことなく組合せの場合の数を求めることができます。また、様々な条件の付いた場合の数でも「和の法則」と「積の法則」を利用し計算していきましょう。

３つのグループに分ける

問題９人を以下の方法で分ける場合の数を求めよ。
${\small (1)}~$３人ずつA、B、Cの３部屋に分ける
${\small (2)}~$３人ずつ３組に分ける
${\small (3)}~$４人、３人、２人に分ける

[ 解答を見る ]

【解答】
${\small (1)}~$1680通り$~~~~~~{\small (2)}~$280通り
${\small (3)}~$1260通り

詳しい解説ページはこちらから↓

３つのグループに分ける

今回は３つのグループに分けるのですが、大事なポイントは「２つのグループに分ける」ときと同じです。「グループに区別があるかどうか」を判断して「グループに区別がない」ときは、(グループの数)！で割る計算をしないといけません。ここをしっかりと押さえておきましょう。

同じものを含む順列

問題次の場合の数を求めよ。
${\small (1)}~$$ a,a,b,b,b,c,d $ の７つの文字を一列に並べる
${\small (2)}~$$ a,a,b,b,c,d,e$ の７つの文字を一列に並べるとき、$ c,d,e$ がこの順になる

[ 解答を見る ]

【解答】
${\small (1)}~$420通り$~~~~~~{\small (2)}~$210通り

詳しい解説ページはこちらから↓

同じものを含む順列

今回は同じものを含む順列を解説していきます。また、「この順になる」条件もおさえておきましょう。

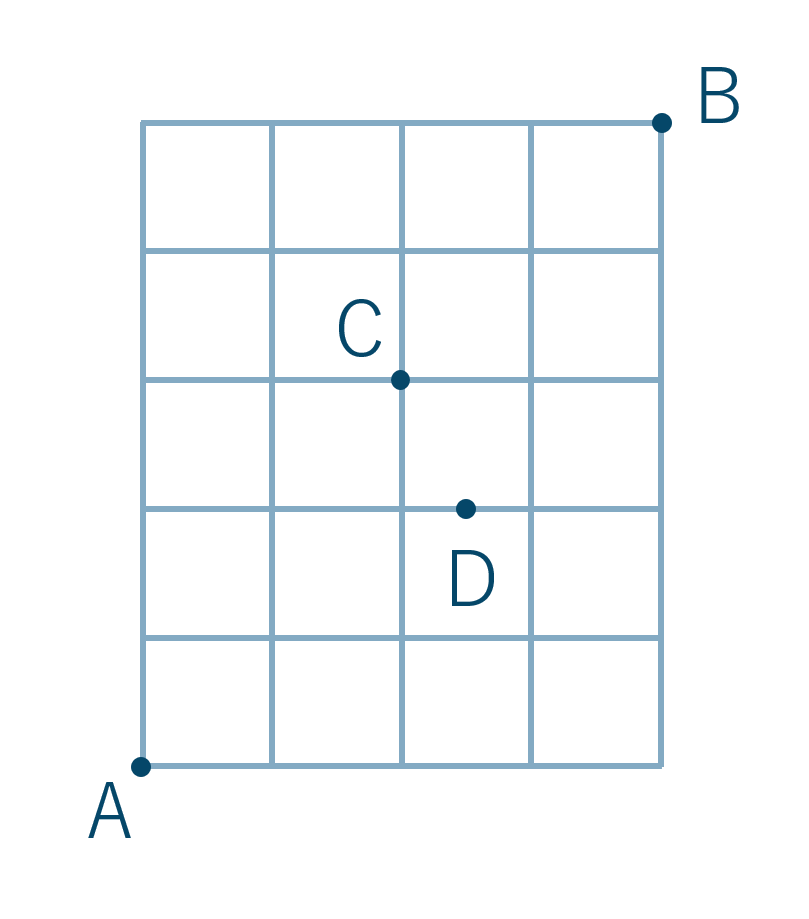
最短経路問題

問題次の図において、次の経路は何通りあるか答えよ。
${\small (1)}~$AからBまでの最短経路
${\small (2)}~$AからBまでの最短経路でCを必ず通る経路
${\small (3)}~$AからBまでの最短経路でDを通らない経路
　

[ 解答を見る ]

【解答】
${\small (1)}~$126通り$~~~~~~{\small (2)}~$60通り$~~~~~~{\small (3)}~$102通り

詳しい解説ページはこちらから↓

最短経路問題

区画に分けられた道路を通って目的地まで行く場合の数を求める問題です。道路を「右に進む」回数と「上に進む」回数を考えて、同じものを含む順列で解く方法をできるようになりましょう！

重複組合せ

問題次の場合の数を求めよ。
${\small (1)}~$６本の同種類のペンをA、B、Cの３つの袋に入れるとき、１本も入らない袋があってよいとき、分け方は何通りあるか。
${\small (2)}~$オレンジ、レモン、ライムがそれぞれ多数ある。これから10個をまとめてセットを作りたい。何通りのセットができるか。

[ 解答を見る ]

【解答】
${\small (1)}~$28通り$~~~~~~{\small (2)}~$66通り

詳しい解説ページはこちらから↓

重複組合せ

今回の重複組合せを解説していきます。この問題は記号Ｈ<を用いて計算するのが一般的ですが、ここではこの記号は使わないで、同じものを含む順列を用いる方法で解いていきます。

等式を満たす自然数の組合せ

問題次の場合の数を求めよ。
${\small (1)}~$$ x+y+z=7$ を満たす $ 0$ 以上の整数の組合せは何通りあるか答えよ。
${\small (2)}~$$ x+y+z=7$ を満たす自然数の組合せは何通りあるか答えよ。

[ 解答を見る ]

【解答】
${\small (1)}~$36通り$~~~~~~{\small (2)}~$15通り

詳しい解説ページはこちらから↓

等式を満たす自然数の組合せ

今回は前回の重複組合せの応用問題である等式を満たす自然数の組合せを解説していきます。問題が等式となっているだけで、解法は重複組合せと同じになります。

確率の基本

問題コインを３枚同時に投げるとき、次の確率を求めよ。
${\small (1)}~$２枚だけ表である確率
${\small (2)}~$表が２枚以上である確率

[ 解答を見る ]

【解答】$${\small (1)}~\frac{3}{8}~~~~~~{\small (2)}~\frac{1}{2}$$

詳しい解説ページはこちらから↓

確率の基本

今回からは確率の問題を解説していきます。確率でも計算の基本は「和の法則と積の法則」です！この計算法則は必ず守りましょう。

さいころの確率

問題さいころを２個同時に投げるとき、次の確率を求めよ。
${\small (1)}~$目の和が８となる確率
${\small (2)}~$目の和が10以下となる確率

[ 解答を見る ]

【解答】$${\small (1)}~\frac{5}{36} ~~~~~~{\small (2)}~\frac{11}{12}$$

詳しい解説ページはこちらから↓

さいころの確率

２個のさいころを振る確率を解説していきましょう。まずは２個のさいころを区別して表を描くことからはじめて、6×6の36マスの表を使って確率を求めましょう。

ボールを取り出す確率

問題赤玉５個と白玉７個が入った袋から同時に３個取り出すとき、次の確率を求めよ。
${\small (1)}~$白玉３個となる確率
${\small (2)}~$赤玉１個、白玉２個となる確率
${\small (3)}~$赤玉２個、白玉１個となる確率

[ 解答を見る ]

【解答】$${\small (1)}~\frac{7}{44} ~~~~~~{\small (2)}~\frac{21}{44} ~~~~~~{\small (3)}~\frac{7}{22}$$

詳しい解説ページはこちらから↓

ボールを取り出す確率

今回は色のついたボールを取り出す確率を解説していきます。どんな問題でも確率であれば基本と解法は変わりません。また、ボールを取り出す場合の数は組合せの記号を用いて解きましょう。

一列に並べる確率

問題男子５人、女子４人が１列に並ぶとき、次の確率を求めよ。
${\small (1)}~$特定の男女が隣り合う
${\small (2)}~$女子が両端にいる
${\small (3)}~$男女が交互に並ぶ

[ 解答を見る ]

【解答】$${\small (1)}~\frac{2}{9} ~~~~~~{\small (2)}~\frac{1}{6} ~~~~~~{\small (3)}~\frac{1}{126}$$

詳しい解説ページはこちらから↓

一列に並べる確率

今回は一列に並べる確率です。一列に並べるのでやはり順列の考え方が重要になってきます。

円形に並べる確率

問題男子３人、女子３人が円卓にする座るとき、次の確率を求めよ。
${\small (1)}~$特定の２人が隣り合う
${\small (2)}~$特定の２人が向い合う
${\small (3)}~$男女が交互に座る

[ 解答を見る ]

【解答】$${\small (1)}~\frac{2}{5} ~~~~~~{\small (2)}~\frac{1}{5} ~~~~~~{\small (3)}~\frac{1}{10}$$

詳しい解説ページはこちらから↓

円形に並べる確率

円順列を用いた確率の問題を見ていきましょう。一列に並べる確率と同じように、それぞれの場合の数の段階では計算せずに確率を計算するときに約分を活用しましょう。

和事象と排反事象

問題1～50までの数字が書かれたカードから、１枚取り出すとき、次の確率を求めよ。
${\small (1)}~$２の倍数または一の位が３である２桁の数
${\small (2)}~$２の倍数または３の倍数

[ 解答を見る ]

【解答】$${\small (1)}~\frac{29}{50} ~~~~~~{\small (2)}~\frac{33}{50}$$

詳しい解説ページはこちらから↓

和事象と排反事象

今回は和事象と排反事象について解説していきます。それぞれの言葉の意味をしっかりと理解しておきましょう。

余事象の確率

問題次の確率を求めよ。
${\small (1)}~$赤玉５個と白玉７個が入った袋から同時に３個取り出すとき、少なくとも赤玉１個を取り出す確率を求めよ。
${\small (2)}~$さいころを２個同時に投げるとき、目の和が３の倍数でない確率を求めよ。

[ 解答を見る ]

【解答】$${\small (1)}~\frac{37}{44} ~~~~~~{\small (2)}~\frac{2}{3}$$

詳しい解説ページはこちらから↓

余事象の確率

今回の余事象について解説していきます。この余事象が使えると非常に計算が簡単になるので、どのようなときに使うかを理解しましょう。

独立試行の確率

問題Aの袋には赤玉３個と白玉２個が、Bの袋には赤玉２個と白玉４個が入っている。Aからは１個、Bからは２個の玉を取り出すとき、取り出した玉の色がすべて赤となる確率を求めよ。

[ 解答を見る ]

【解答】$$~~~~~~\frac{1}{25}$$

詳しい解説ページはこちらから↓

独立試行の確率

今回は独立試行について説明します。どのような試行かを理解して、解けるようになりましょう。

反復試行の確率①（コイン）

問題１枚のコインを５回連続して投げるとき、次の確率を求めよ。
${\small (1)}~$表がちょうど４回出る
${\small (2)}~$表がちょうど３回出る

[ 解答を見る ]

【解答】$${\small (1)}~\frac{5}{32} ~~~~~~{\small (2)}~\frac{5}{16}$$

詳しい解説ページはこちらから↓

反復試行の確率①（コイン）

今回は同じ試行を繰り返す反復試行の確率を説明します。定期テストだけでなく、入試問題にも頻出ですので練習してできるようになりましょう！

反復試行の確率②（さいころ）

問題１個のさいころを５回連続して投げるとき、次の確率を求めよ。
${\small (1)}~$３の倍数の目が2回だけ出る
${\small (2)}~$３の倍数の目が3回だけ出る
${\small (3)}~$少なくとも１回３の倍数の目が出る

[ 解答を見る ]

【解答】$${\small (1)}~\frac{80}{243} ~~~~~~{\small (2)}~\frac{40}{243} ~~~~~~{\small (3)}~\frac{211}{243}$$

詳しい解説ページはこちらから↓

反復試行の確率②（さいころ）

今回はさいころを複数回振るときの反復試行の確率を解説していきます。反復試行の基本は前回と同じになります。

○勝先取の確率

問題AとBが試合をし、先に３勝した方が優勝とする。Aが勝つ確率が $ {\Large \frac{3}{4}} $ のとき、Aが優勝する確率を求めよ。

[ 解答を見る ]

【解答】$$~~~~~~\frac{459}{512}$$

詳しい解説ページはこちらから↓

◯勝先取の確率

プロ野球の日本シリーズは先に４勝したチームが優勝となるルールが採用されています。このような◯勝先取の確率の求め方を解説していきます。ポイントは「最後の試合は優勝チームが必ず勝つ」です。

点が動く確率

問題数直線上に点Pが原点にあり、さいころを投げて５以上の目が出ると正の方向に２進み、それ以外が出ると負の方向に１進む。さいころを３回投げたとき点Pが次の位置にある確率を求めよ。
${\small (1)}~$原点の位置にある
${\small (2)}~$座標3の位置にある

[ 解答を見る ]

【解答】$${\small (1)}~\frac{4}{9}~~~~~~{\small (2)}~\frac{2}{9}$$

詳しい解説ページはこちらから↓

点が動く確率

さいころを振り出た目によって点が数直線上を動く確率を解説していきます。複数回さいころを振ることになるので反復試行の確率となります。また、点が最後にどこでストップするかが重要となります。

条件付き確率

問題ある学校で数学が好きな生徒は40%で、英語が好きな生徒は60%で、両方好きな生徒は30%である。次の確率を求めよ。
${\small (1)}~$ある生徒が数学を好きとわかっていて、その生徒が英語も好きな確率
${\small (2)}~$ある生徒が英語を好きとわかっていて、その生徒が数学も好きな確率

[ 解答を見る ]

【解答】$${\small (1)}~\frac{3}{4}~~~~~~{\small (2)}~\frac{1}{2}$$

詳しい解説ページはこちらから↓