このページは「高校数学Ａ：図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないときは、こちらのページから類題を探しましょう！
また、「解答を見る」クリックすると答えのみ表示されます。問題演習としても使えるようになっています。
数学Ａ：図形の性質の公式一覧はこちらから↓
教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします！
【問題一覧】数学Ａ：図形の性質
内分点と外分点の位置
\({\small (1)}\) 線分 \({\rm AB}\) を \(3:1\) に内分する点 \({\rm P}\)
\({\small (2)}\) 線分 \({\rm AB}\) を \(2:1\) に外分する点 \({\rm Q}\)
\({\small (3)}\) 線分 \({\rm AB}\) を \(1:3\) に外分する点 \({\rm R}\)
[ 解答を見る ]
詳しい解説ページはこちらから↓
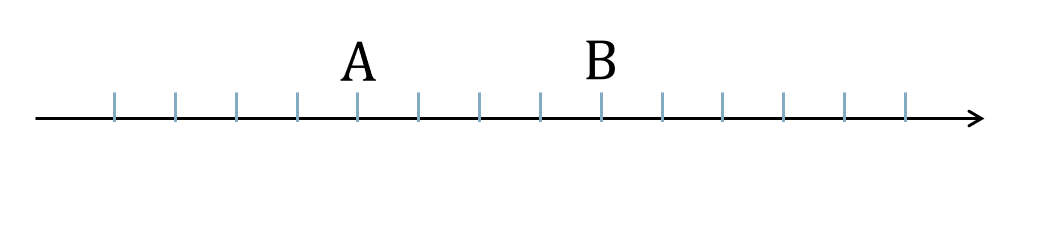
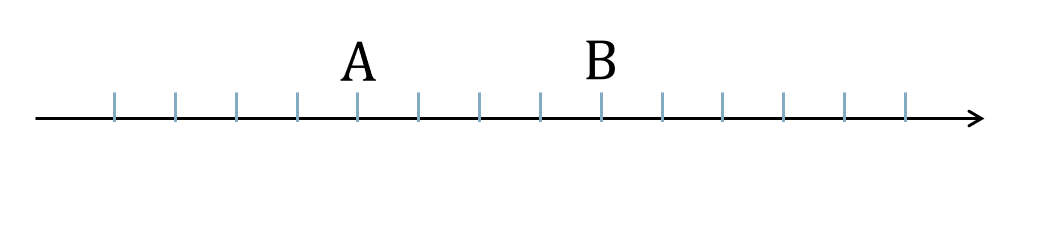
中点連結定理と平行線と比
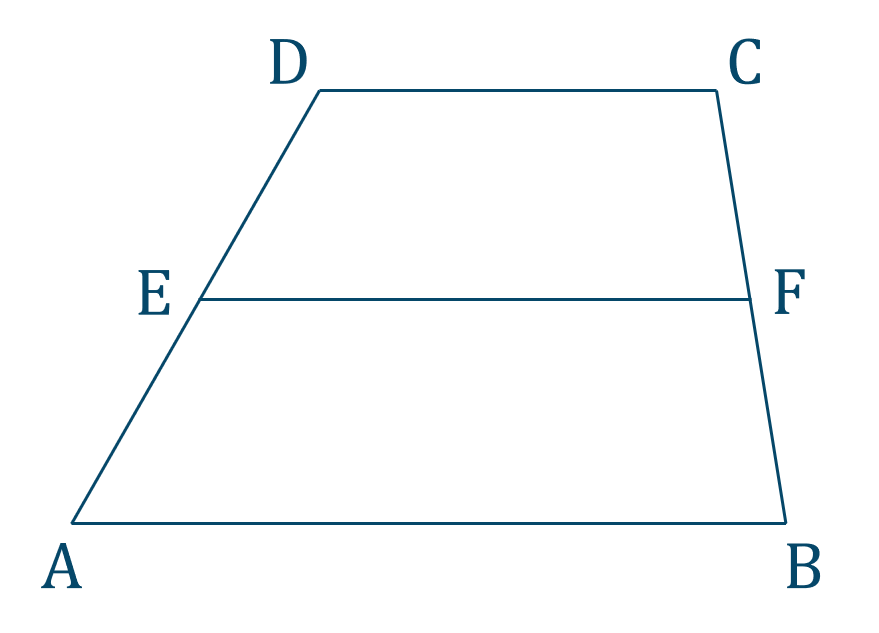
\({\small (1)}\) 次の台形 \({\rm ABCD}\) が \({\rm AB}\parallel{\rm DC}\) \(,\) \({\rm AB}=13\) \(,\) \({\rm CD}=7\) であり、点 \({\rm E~,~F}\) がそれぞれ \({\rm AD~,~BC}\) の中点とし、\({\rm AB}\parallel{\rm EF}\) であるとき、\({\rm EF}\) の長さを求めよ。
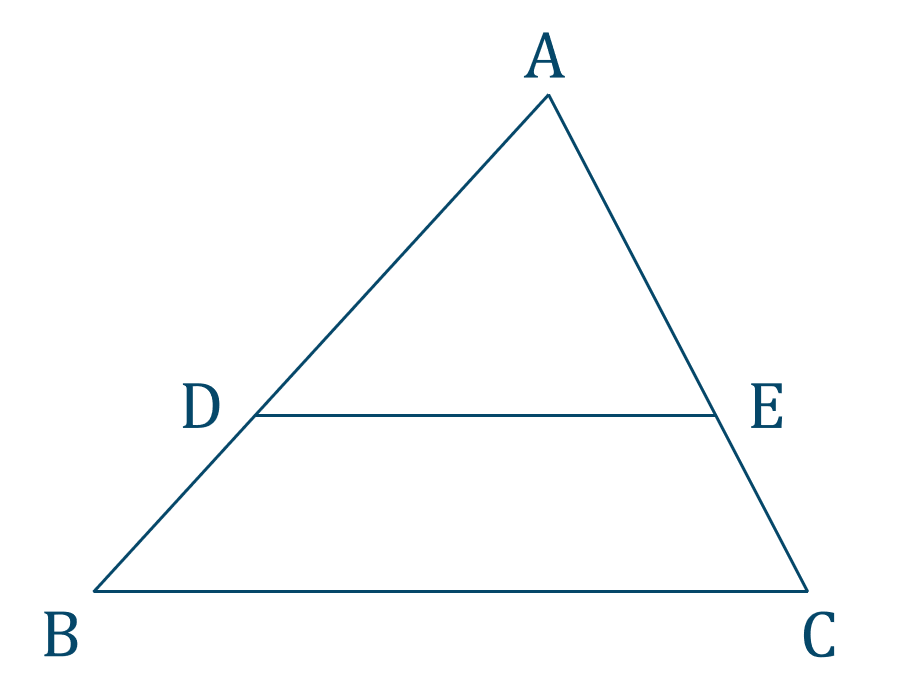
\({\small (2)}\) 次の \(\triangle {\rm ABC}\) について、\({\rm BC}\parallel{\rm DE}\) \(,\) \({\rm AD}=3\) \(,\) \({\rm DB}=2\) \(,\) \({\rm AE}=2\) \(,\) \({\rm BC}=6\) のとき、\({\rm EC}\) と \({\rm DE}\) の長さを求めよ。
[ 解答を見る ]
【解答】$${\small (1)}~{\rm EF}=10$$$${\small (2)}~{\rm EC}=\frac{4}{3}~,~{\rm DE}=\frac{18}{5}$$
詳しい解説ページはこちらから↓
角の二等分線と比
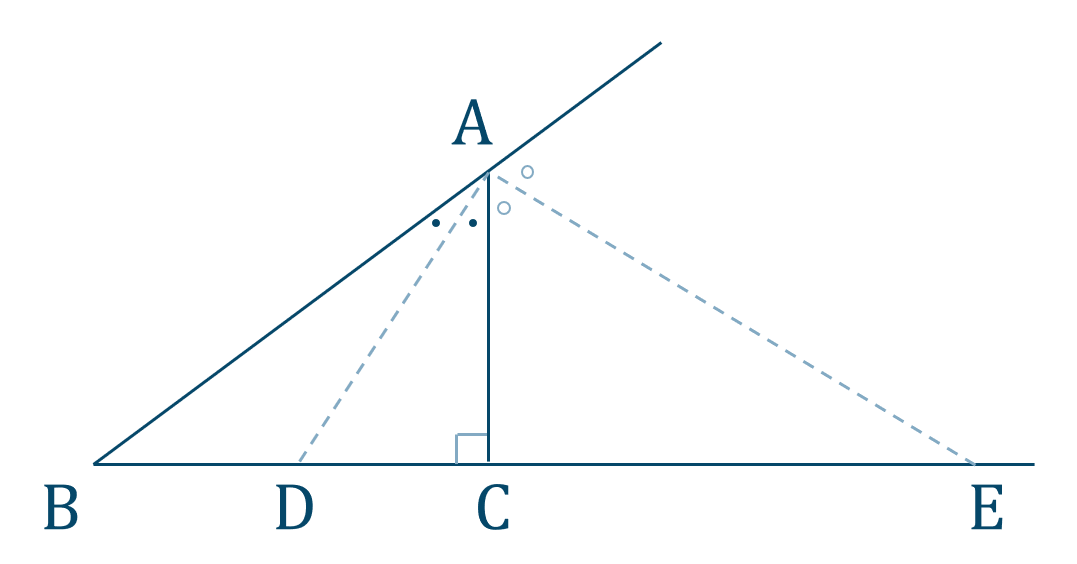
[ 解答を見る ]
【解答】$$~~~{\rm DE}=\frac{15}{2}$$
詳しい解説ページはこちらから↓
三角形の外心
$${\small (1)}~\angle{\rm BOC}$$$${\small (2)}~\angle{\rm OCB}$$
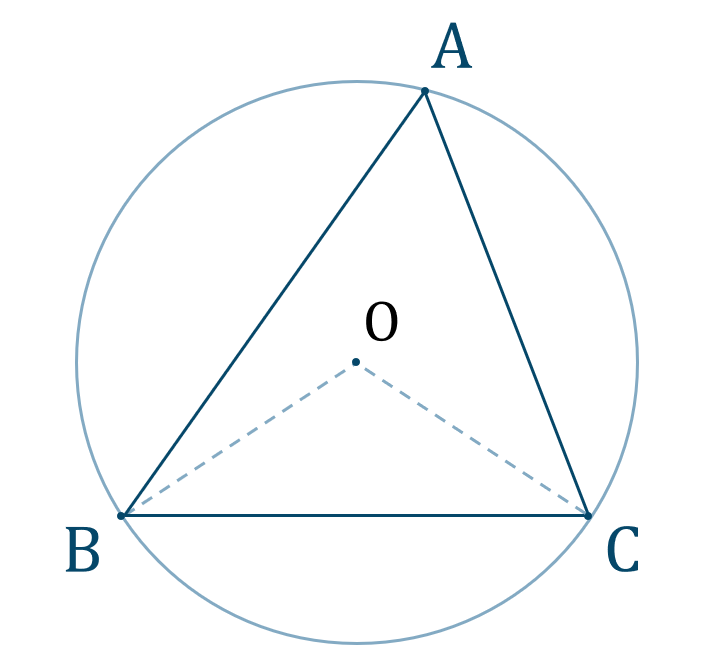
[ 解答を見る ]
【解答】$${\small (1)}~\angle{\rm BOC}=160^\circ$$$${\small (2)}~\angle{\rm OCB}=10^\circ$$
詳しい解説ページはこちらから↓
三角形の内心
$${\small (1)}~\angle{\rm BIC}$$$${\small (2)}~\angle{\rm AST}$$$${\small (3)}~\angle{\rm SIT}$$
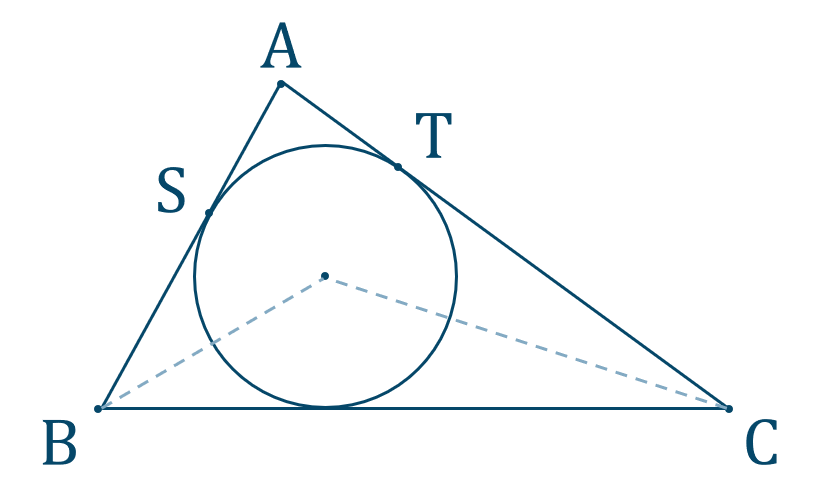
[ 解答を見る ]
【解答】$${\small (1)}~\angle{\rm BIC}=130^\circ$$$${\small (2)}~ \angle{\rm AST}=50^\circ$$$${\small (1)}~\angle{\rm SIT}=100^\circ$$
詳しい解説ページはこちらから↓
三角形の垂心
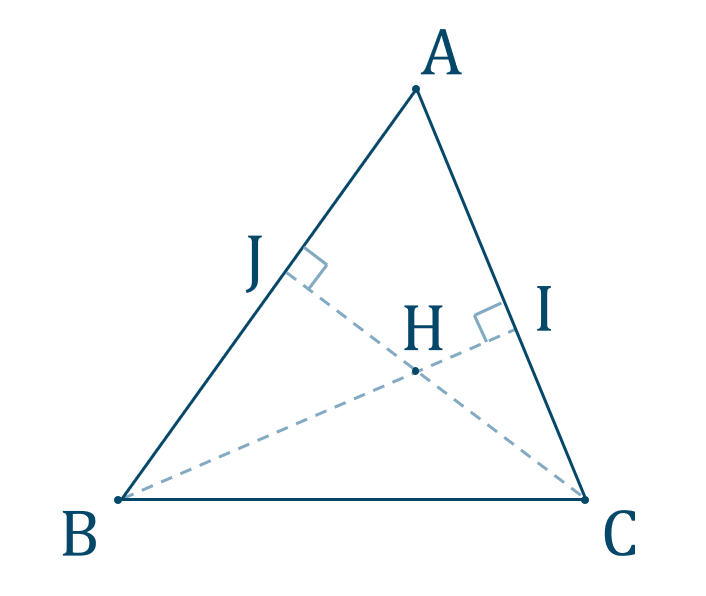
[ 解答を見る ]
【解答】$$~~~\angle{\rm BHC}=140^\circ$$
詳しい解説ページはこちらから↓
三角形の重心
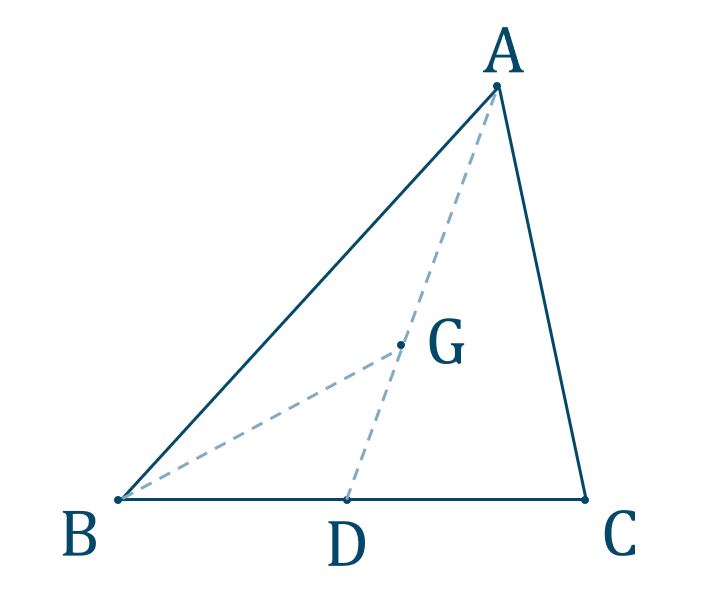
[ 解答を見る ]
【解答】$$~~~~~~\triangle {\rm ABC}:\triangle {\rm ABD}:\triangle {\rm ABG}:\triangle {\rm GBD}$$$$~=6:3:2:1$$
詳しい解説ページはこちらから↓
チェバの定理
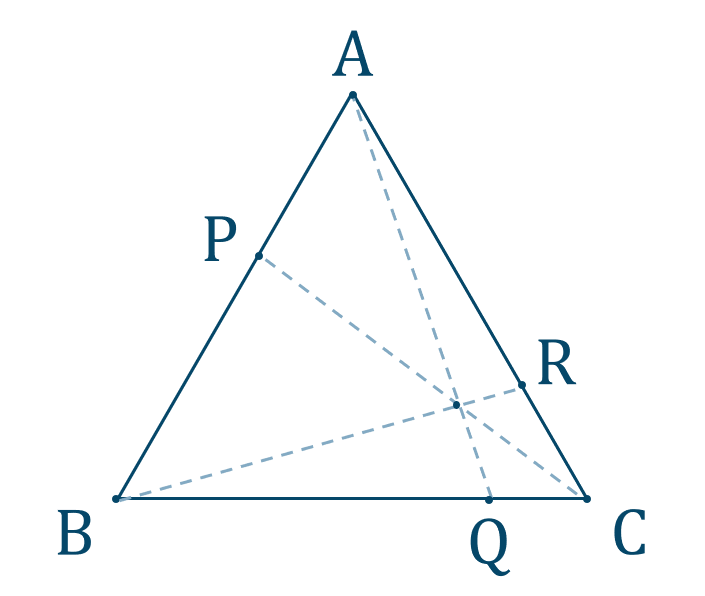
[ 解答を見る ]
【解答】$$~~~{\rm BQ}:{\rm QC}=6:1$$
詳しい解説ページはこちらから↓
メネラウスの定理
$${\small (1)}~ {\rm BQ}:{\rm QC}$$$${\small (2)}~ {\rm PQ}:{\rm QR}$$
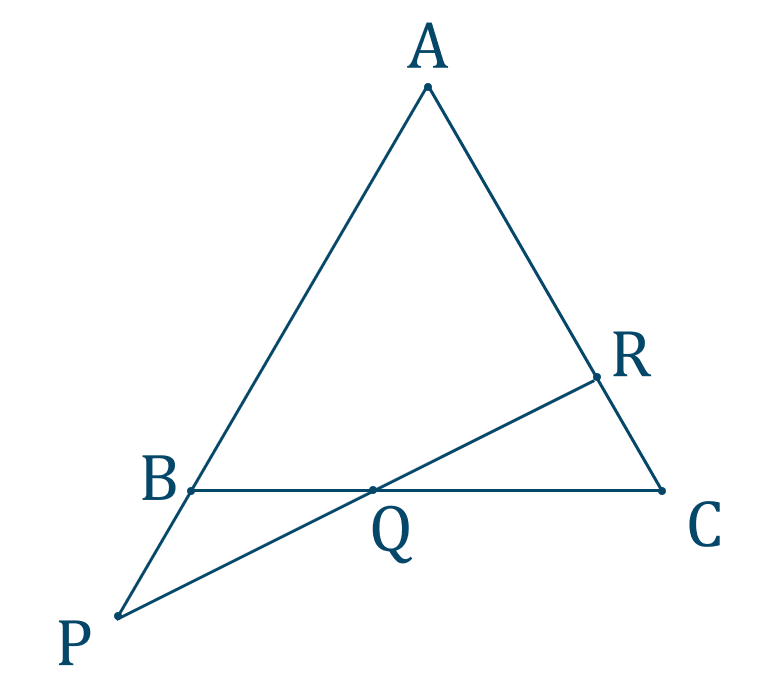
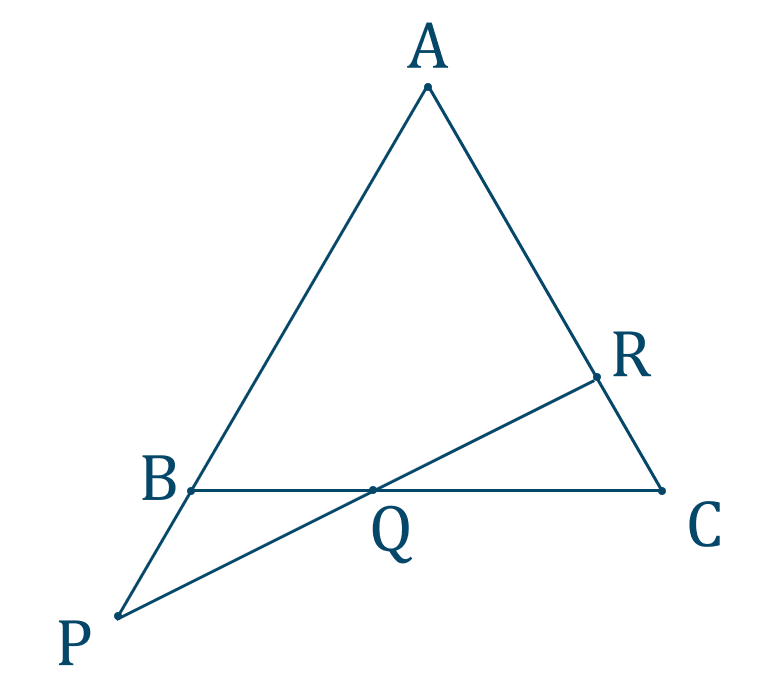
[ 解答を見る ]
【解答】$${\small (1)}~{\rm BQ}:{\rm QC}=8:7$$$${\small (2)}~{\rm PQ}:{\rm QR}=2:1$$
詳しい解説ページはこちらから↓
三角形の辺と角の大小関係
\({\small (1)}\) \(a=8\) \(,\) \(b=6\) \(,\) \(c=3\) のとき、３つの角の大小を調べよ。
\({\small (2)}\) \(\angle{\rm A}=110^\circ\) \(,\) \(b=4\) \(,\) \(c=10\) のとき、３つの角の大小を調べよ。
\({\small (3)}\) \(\angle{\rm A}=80^\circ\) \(,\) \(\angle{\rm B}=30^\circ\) のとき、３つの辺の大小を調べよ。
[ 解答を見る ]
【解答】$${\small (1)}~{\small\angle}{\rm A}>{\small\angle}{\rm B}>{\small\angle}{\rm C}$$$${\small (2)}~{\small\angle}{\rm A}>{\small\angle}{\rm C}>{\small\angle}{\rm B}$$$${\small (3)}~a>c>b$$
詳しい解説ページはこちらから↓
三角形になるための条件
[ 解答を見る ]
【解答】$${\small (1)}~3<x<7$$$${\small (2)}~1<x<3$$
詳しい解説ページはこちらから↓
円周角と中心角
\({\small (1)}\) 次の図の角度 \(x~,~y\) の値を求めよ。
\({\large ①}\)
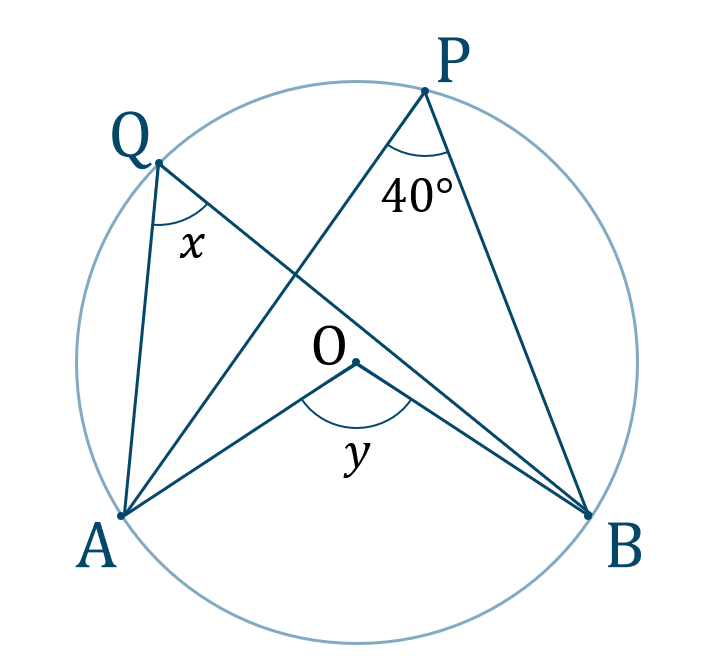
\({\large ②}\)
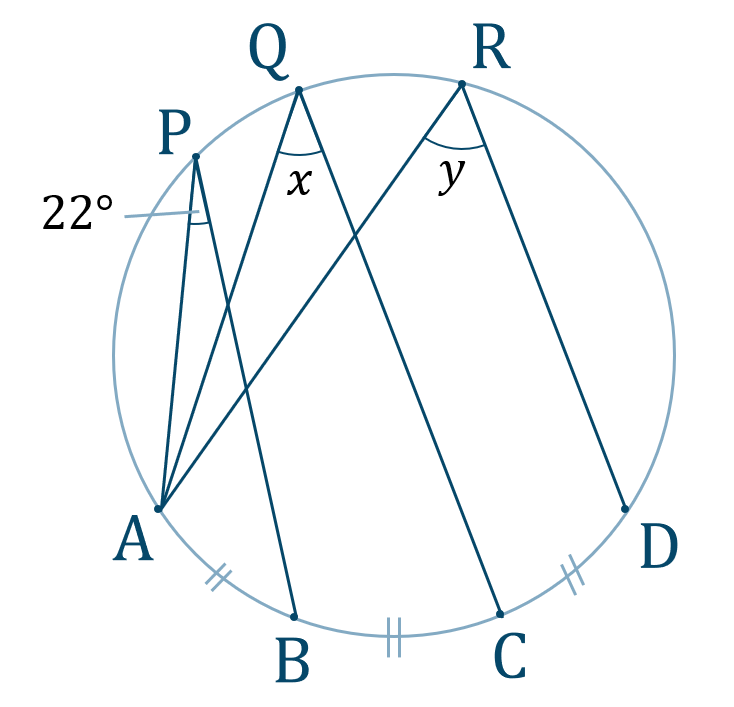
\({\large ③}\)
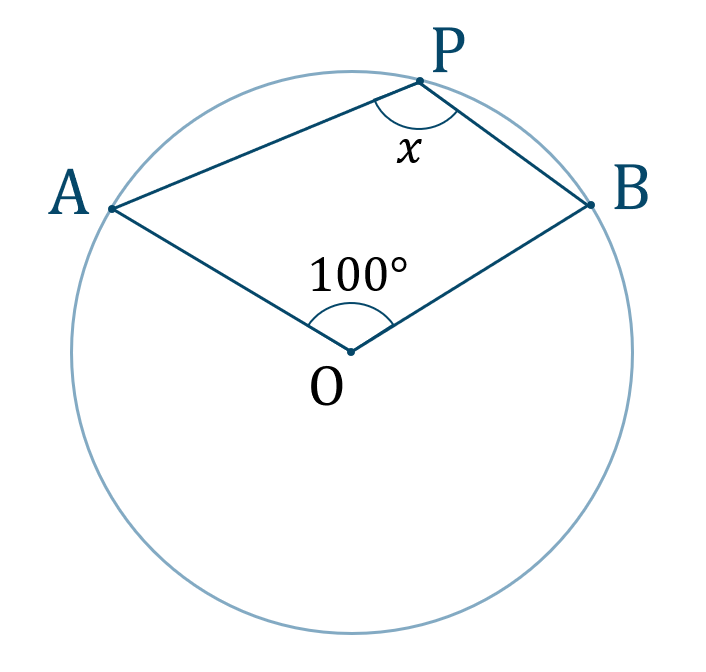
\({\small (2)}\) 円 \({\rm O}\) の円上に３点 \({\rm A}\) \(,\) \({\rm B}\) \(,\) \({\rm C}\) をとり、次の比が成り立つとき、$$~~~{\rm AB}:{\rm BC}:{\rm CA}=3:4:5$$\(\angle{\rm ACB}\) \(,\) \(\angle{\rm BAC}\) \(,\) \(\angle{\rm ABC}\) の値を求めよ。
[ 解答を見る ]
【解答】$${\small (1)}$$$$~{\large ①}~x=40^\circ~,~y=80^\circ$$$$~{\large ②}~x=44^\circ~,~y=66^\circ$$$$~{\large ③}~x=130^\circ$$$${\small (2)}~\angle{\rm ABC}=75^\circ~,~\angle{\rm ACB}=45^\circ$$$$~~~\angle{\rm BAC}=60^\circ$$
詳しい解説ページはこちらから↓
円に内接する四角形と角
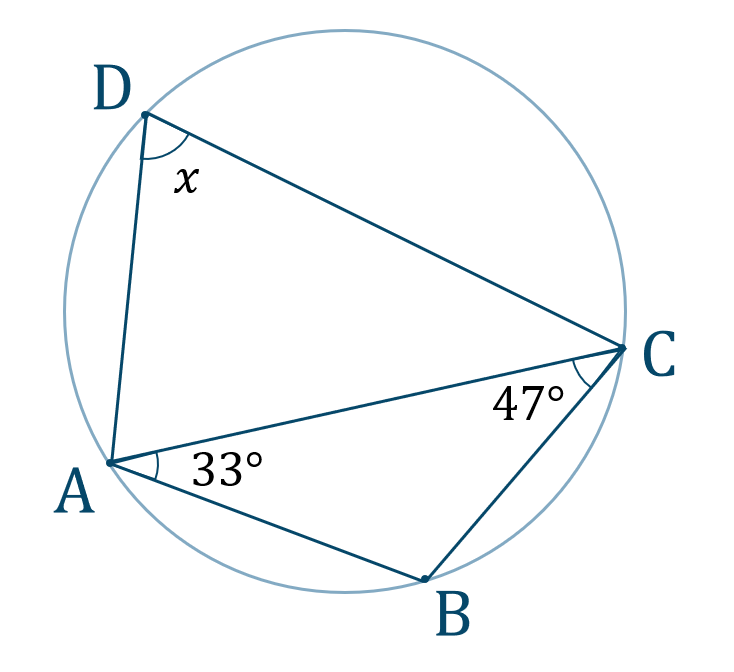
\({\small (1)}\) 次の図の角度 \(x~,~y\) の値を求めよ。
\({\large ①}\)
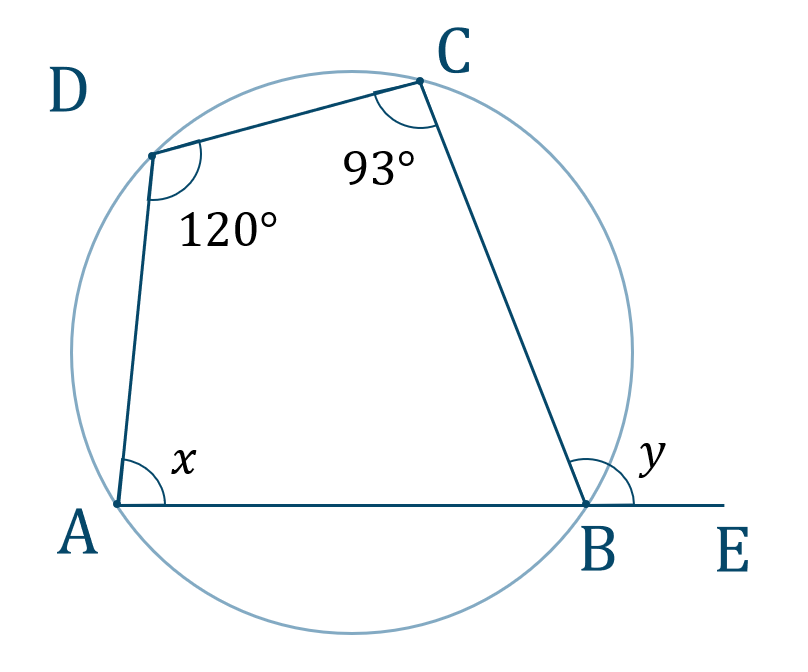
\({\large ②}\)
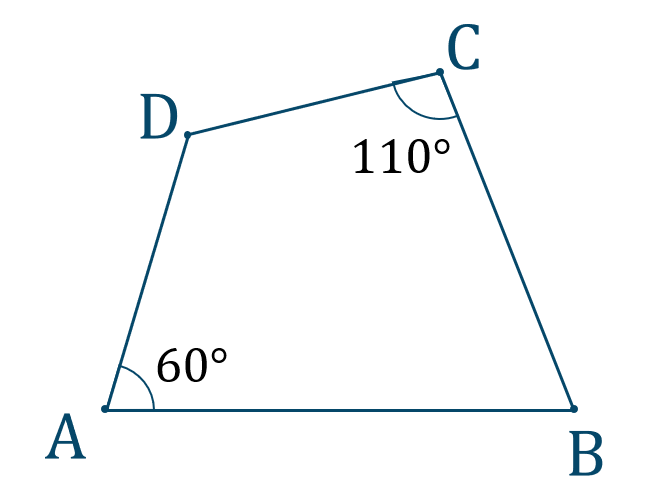
\({\small (2)}\) 次の四角形の中で円に内接するかどうか調べよ。
\({\large ①}\)
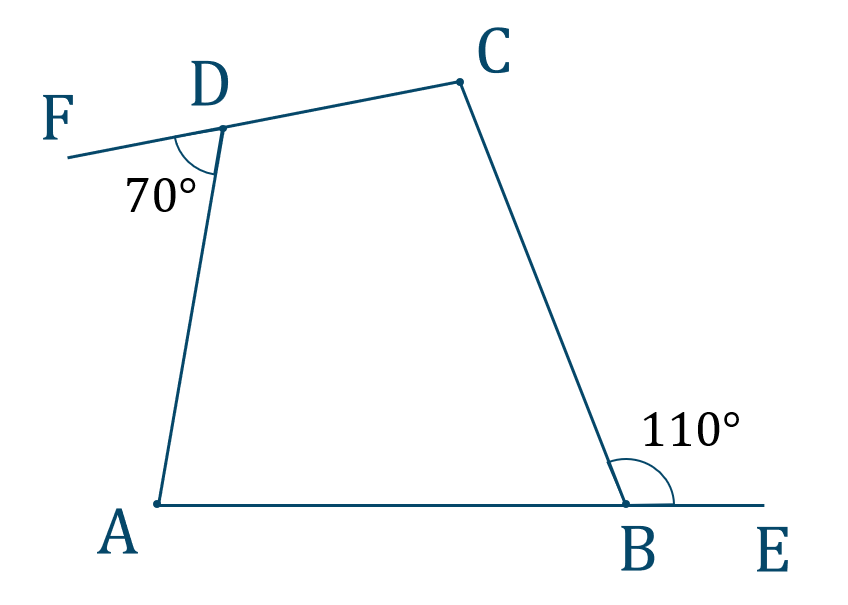
\({\large ②}\)
\({\large ③}\)
[ 解答を見る ]
【解答】$${\small (1)}$$$$~{\large ①}~x=87^\circ~,~y=120^\circ$$$$~{\large ②}~x=80^\circ$$$${\small (2)}$$②、③が円に内接する四角形である。
詳しい解説ページはこちらから↓
接弦定理
\({\small (1)}\)
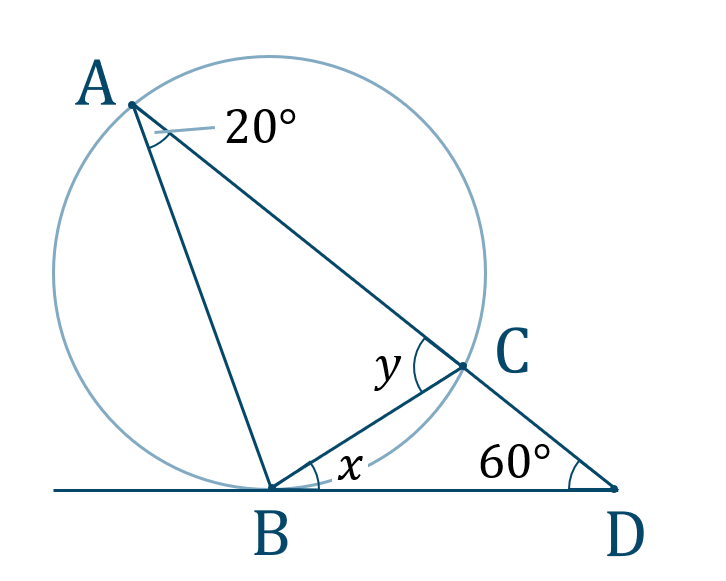
\({\small (2)}\)
[ 解答を見る ]
【解答】$${\small (1)}~x=20^\circ~,~y=80^\circ$$$${\small (2)}~x=62^\circ~,~y=45^\circ$$
詳しい解説ページはこちらから↓
内接円と接線の条件
\({\small (1)}\) \({\rm BC}\) の長さを求めよ。
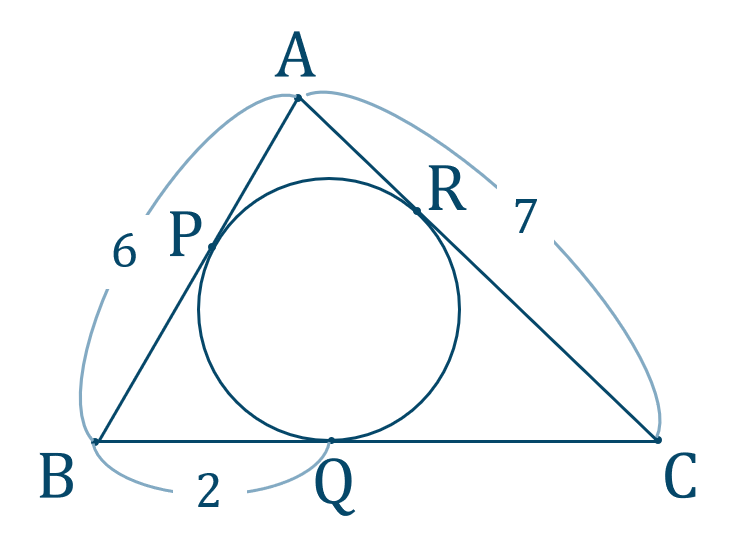
\({\small (2)}\) 内接円の半径 \(r\) を求めよ。
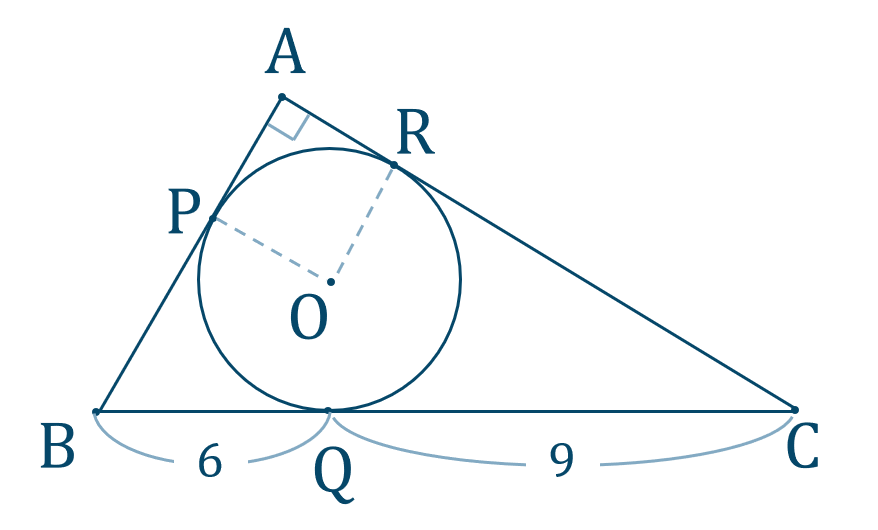
[ 解答を見る ]
【解答】$${\small (1)}~{\rm BC}=5$$$${\small (2)}~r=3$$
詳しい解説ページはこちらから↓
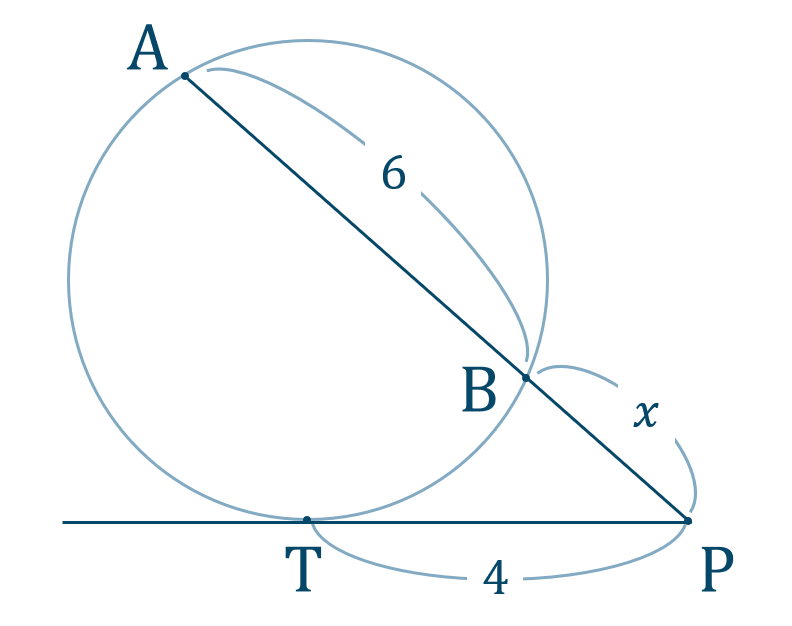
方べきの定理
\({\small (1)}\)
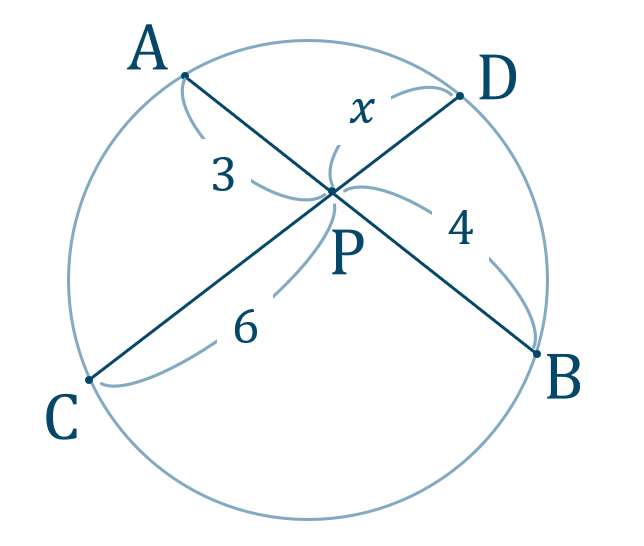
\({\small (2)}\)
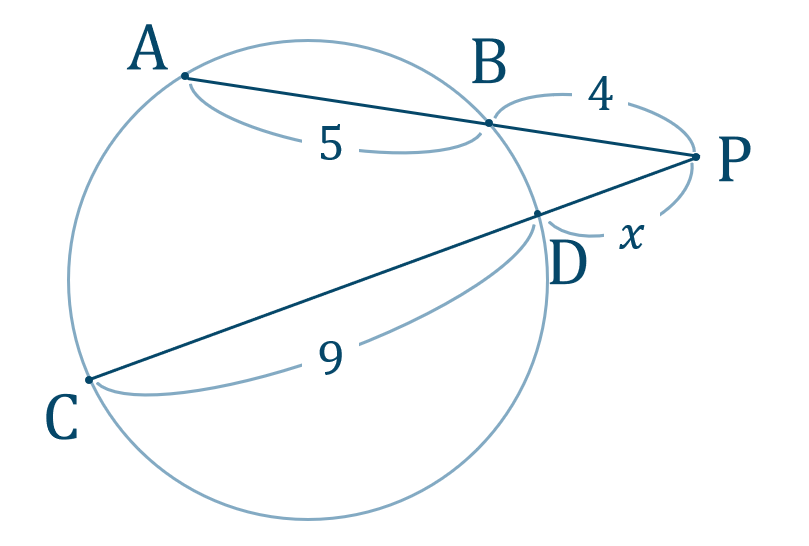
\({\small (3)}\)
[ 解答を見る ]
【解答】$${\small (1)}~x=2$$$${\small (2)}~x=3$$$${\small (3)}~x=2$$
詳しい解説ページはこちらから↓
２つの円の位置関係と共通接線
[ 解答を見る ]
【解答】
\({\small (1)}\) 半径 \(3\) の円が半径 \(7\) の円の内部にあり、共通接線は０本となります。
\({\small (2)}\) 半径 \(3\) の円と半径 \(7\) の円は外接しており、共通接線は３本となります。
\({\small (3)}\) 半径 \(3\) の円と半径 \(7\) の円は離れており、共通接線は４本となります。
\({\small (4)}\) 半径 \(3\) の円と半径 \(7\) の円は２点で交わり、共通接線は２本となります。
\({\small (5)}\) 半径 \(3\) の円と半径 \(7\) の円は内接しており、共通接線は１本となります。
詳しい解説ページはこちらから↓
共通接線の長さ
\({\small (1)}\) 共通接線 \({\rm AB}\) の線分の長さ
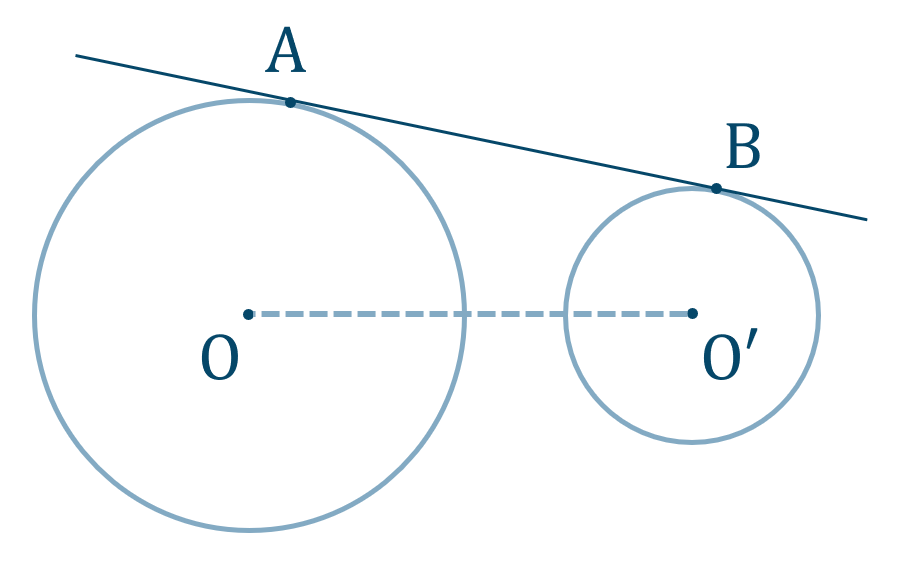
\({\small (2)}\) 共通接線 \({\rm CD}\) の線分の長さ
[ 解答を見る ]
【解答】$${\small (1)}~{\rm AB}=2\sqrt{35}$$$${\small (2)}~{\rm CD}=4\sqrt{5}$$
詳しい解説ページはこちらから↓
作図の基本
\({\small (1)}\) 線分 \({\rm AB}\) の垂直二等分線
\({\small (2)}\) 角 \(\angle{\rm AOB}\) の二等分線
\({\small (3)}\) 点 \({\rm A}\) を通り、直線に垂直な直線
\({\small (4)}\) 点 \({\rm A}\) を通り、直線に平行な直線
[ 解答を見る ]
詳しい解説ページはこちらから↓
内分点と外分点の作図
\({\small (1)}\) 線分 \({\rm AB}\) を \(1:3\) に内分する点
\({\small (2)}\) 線分 \({\rm AB}\) を \(3:1\) に外分する点
分数倍の作図
平方根の値の作図
空間図形の位置関係
\({\small (1)}\) 線分 \({\rm AB}\) に平行な辺
\({\small (2)}\) 線分 \({\rm AG}\) とねじれの位置にある辺
\({\small (3)}\) 線分 \({\rm AB}\) と垂直な辺と面
\({\small (4)}\) 面 \({\rm ABCD}\) と平行な辺と面
[ 解答を見る ]
【解答】
\({\small (1)}\)
辺 \({\rm DC}\) \(,\) \({\rm EF}\) \(,\) \({\rm HG}\)
\({\small (2)}\)
辺 \({\rm BC}\) \(,\) \({\rm DC}\) \(,\) \({\rm BF}\) \(,\) \({\rm EF}\) \(,\) \({\rm EH}\) \(,\) \({\rm DH}\)
\({\small (3)}\)
辺 \({\rm AD}\) \(,\) \({\rm AE}\) \(,\) \({\rm BC}\) \(,\) \({\rm BF}\)
面 \({\rm AEHD}\) \(,\) \({\rm BFGC}\)
\({\small (4)}\)
辺 \({\rm EF}\) \(,\) \({\rm GH}\) \(,\) \({\rm EH}\) \(,\) \({\rm FG}\)
面 \({\rm EFGH}\)
詳しい解説ページはこちらから↓
