【公式一覧】数学Ａ：図形の性質

このページは「高校数学Ａ：図形の性質」の公式や解法の手順をまとめたページとなります。
目次の単元をクリックすると各単元に飛べますので活用してください。また、問題と詳しい解説のリンクもありますので公式の使い方を詳しく知りたいときにそちらも参考にしましょう。

【問題一覧】数学Ａ：図形の性質

このページは「高校数学Ａ：図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないとき...

教科書より詳しい高校数学「よりくわ」の公式Line@アカウントです。キーワードを入力するとサイトのURLや公式の画像などを検索できますので、友達登録よろしくお願いします！

【公式一覧】数学Ａ：図形の性質

【公式一覧】数学Ａ：図形の性質

内分点と外分点の位置

Point：内分点と外分点・内分点
線分 ${\rm AB}$ を $m:n$ に内分する点 ${\rm P}$

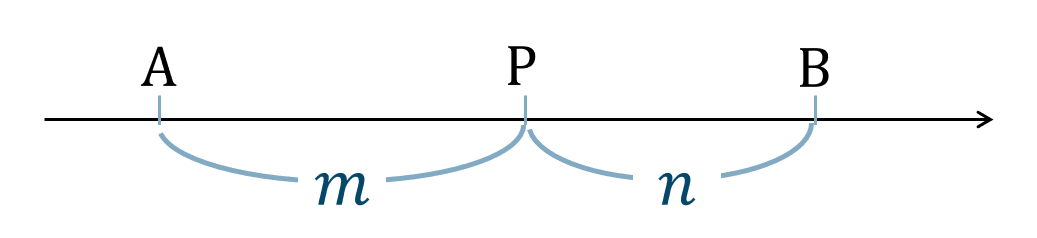
図のように ${\rm A}~\to~{\rm B}$ を $m$ と $n$ に分けて進んだと考えましょう。

・外分点
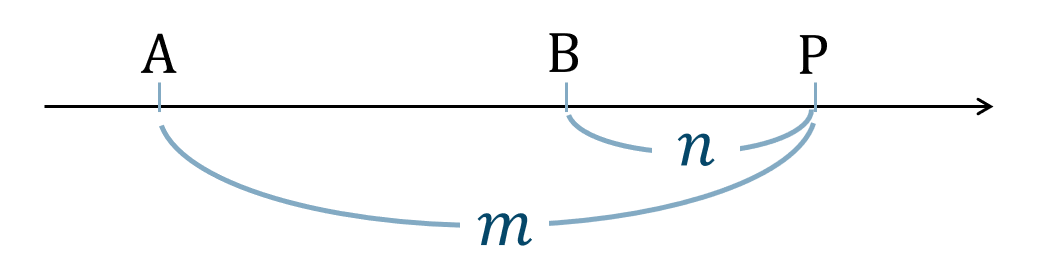
線分 ${\rm AB}$ を $m:n$ に外分する点 ${\rm Q}$
( ⅰ ) $m>n$ のとき、
${\rm A}~\to~{\rm B}$ を $m$ 進んで $n$ 戻ると考えて、

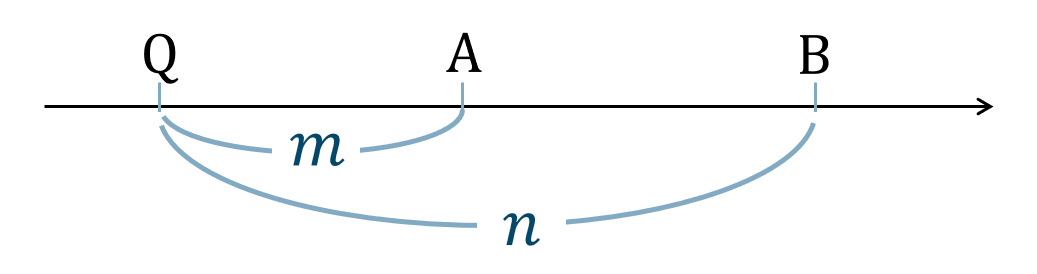
( ⅱ ) $m<n$ のとき、
${\rm A}~\to~{\rm B}$ を $m$ 戻り $n$ 進むと考えて、

問題と詳しい解説はこちらから

内分点と外分点の位置

今回は数直線上の内分点と外分点の位置について解説していきます。線分の並びと内分外分の順番に注意して解いていきましょう。

中点連結定理と平行線と比

Point：平行線と比$\triangle {\rm ABC}$ と ${\rm AB}$ $,$ ${\rm AC}$ 上の点 ${\rm D~,~E}$ において、

$${\small (1)}~{\rm DE}\parallel{\rm BC}~\Leftrightarrow~{\rm AD}:{\rm AB}={\rm AE}:{\rm AC}$$$${\small (2)}~{\rm DE}\parallel{\rm BC}~\Leftrightarrow~{\rm AD}:{\rm DB}={\rm AE}:{\rm EC}$$$${\small (3)}~{\rm DE}\parallel{\rm BC}~\Leftrightarrow~{\rm AD}:{\rm AB}={\rm DE}:{\rm BC}$$

Point：中点連結定理

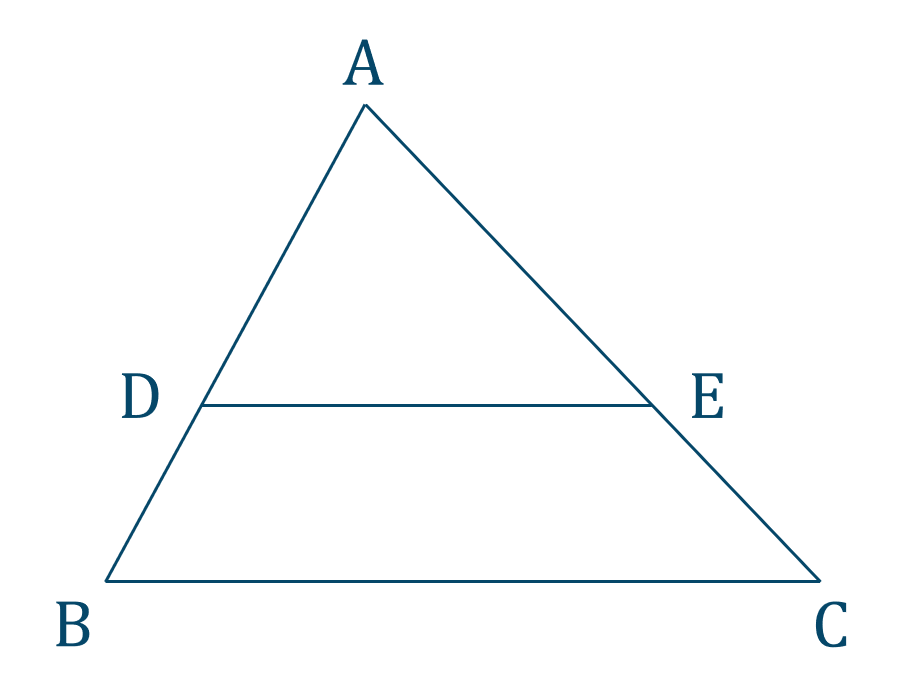
$\triangle {\rm ABC}$ と ${\rm AB}$ $,$ ${\rm AC}$ のそれぞれの中点を ${\rm M~,~N}$ において、

$${\rm AM}={\rm MB}~,~{\rm AN}={\rm NC}$$$$~~~~\Leftrightarrow~{\rm MN}\parallel{\rm BC}~,~{\rm MN}=\frac{1}{2}{\rm BC}$$

問題と詳しい解説はこちらから

中点連結定理と平行線と比

今回は中点連結定理と平行線と比の関係について解説していきます。それぞれの公式をしっかりと覚えておきましょう。

角の二等分線と比

Point：内角の二等分線と比$\triangle {\rm ABC}$ と $\angle{\rm A}$ の内角の二等分線と直線 ${\rm BC}$ との交点を ${\rm D}$ とすると、

$${\rm AB}:{\rm AC}={\rm BD}:{\rm DC}$$

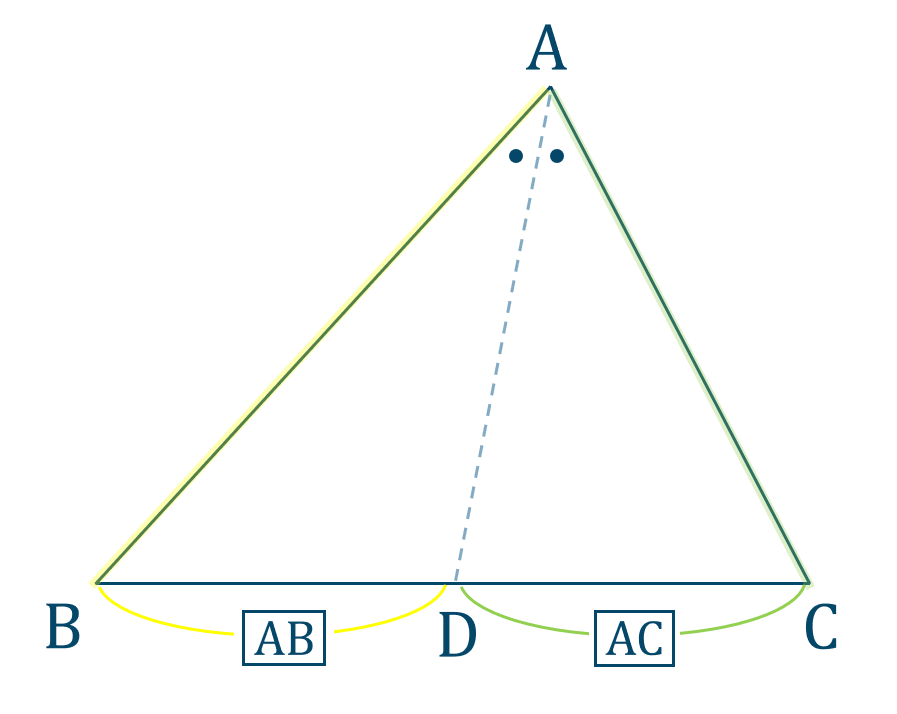
「${\rm A \to B}$ と ${\rm B \to D}$ の比」と
「${\rm A \to C}$ と ${\rm C \to D}$ の比」と覚えましょう。

Point：外角の二等分線と比

$\triangle {\rm ABC}$ と $\angle{\rm A}$ の外角の二等分線と直線 ${\rm BC}$ との交点を ${\rm E}$ とすると、

$${\rm AB}:{\rm AC}={\rm BE}:{\rm CE}$$

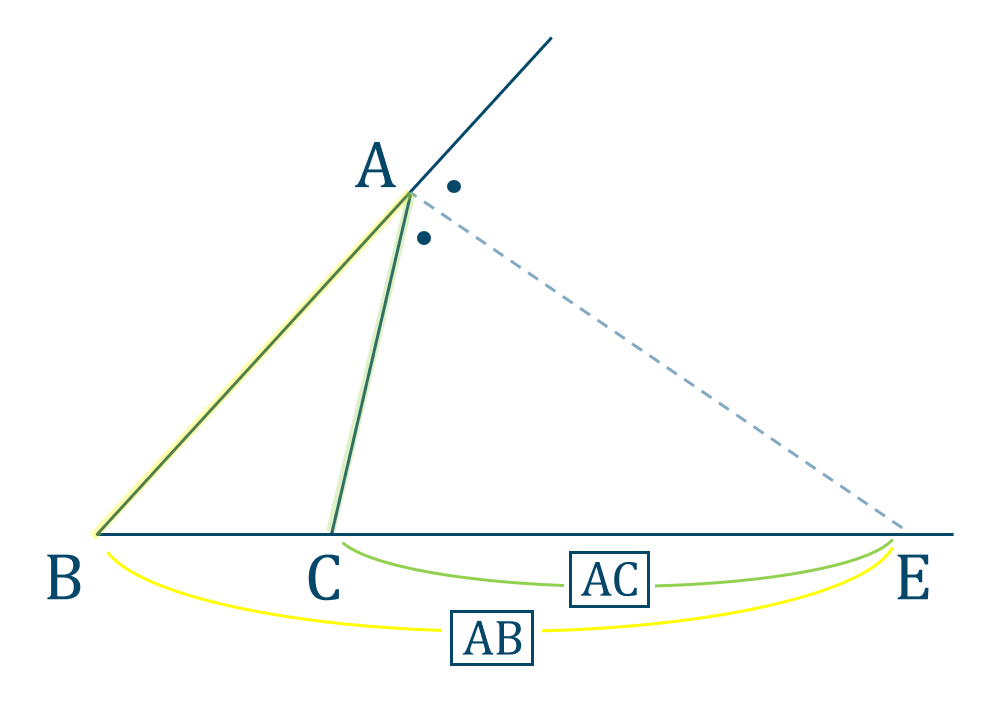
「${\rm A \to B}$ と ${\rm B \to E}$ の比」と
「${\rm A \to C}$ と ${\rm C \to E}$ の比」と覚えましょう。

問題と詳しい解説はこちらから

角の二等分線と比

今回は角の二等分線と比の関係について解説していきます。内角のときと外角のときの公式をそれぞれしっかりと覚えておきましょう。

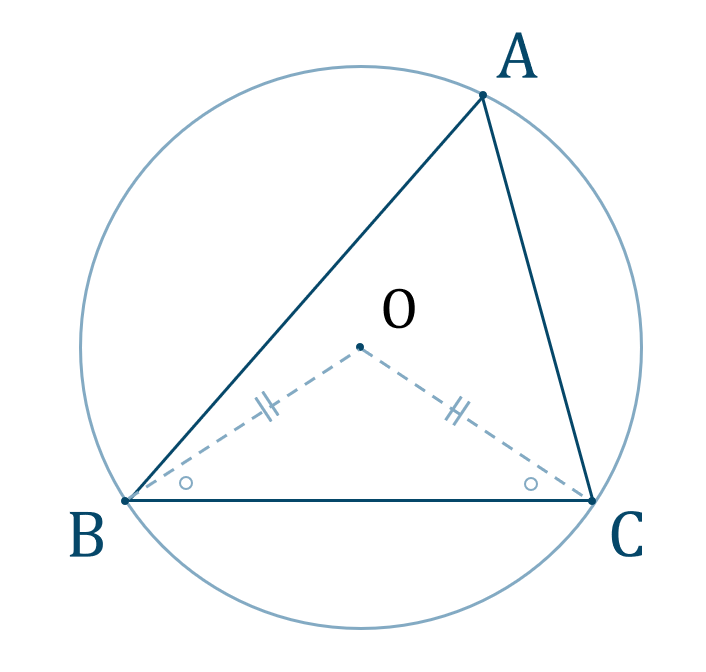
三角形の外心

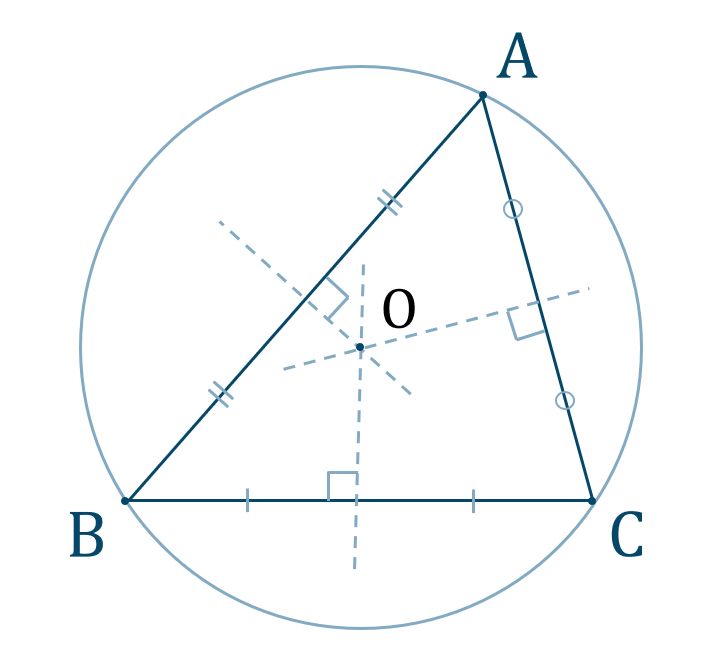
Point：三角形の外心【定理】三角形の３辺の垂直二等分線は１点で交わる。

このときの交点 ${\rm O}$ を中心とする円を $\triangle {\rm ABC}$ の外接円といい、点 ${\rm O}$ を外心という。

・外心についての性質
( ⅰ ) 円周角と中心角の定理が成り立つ

$$\angle{\rm BOC}=2\angle{\rm BAC}$$

( ⅱ ) 外心 ${\rm O}$ から頂点に引いた線分は半径となるので、

$${\rm OB}={\rm OC}$$

これより、$\triangle {\rm OBC}$ は二等辺三角形となります。よって、底角が等しくなるので、

$$\angle{\rm OBC}=\angle{\rm OCB}$$

問題と詳しい解説はこちらから

三角形の外心

三角形の五心の１つである外心について解説していきます。外接円の性質についてもあわせて覚えておきましょう。

三角形の内心

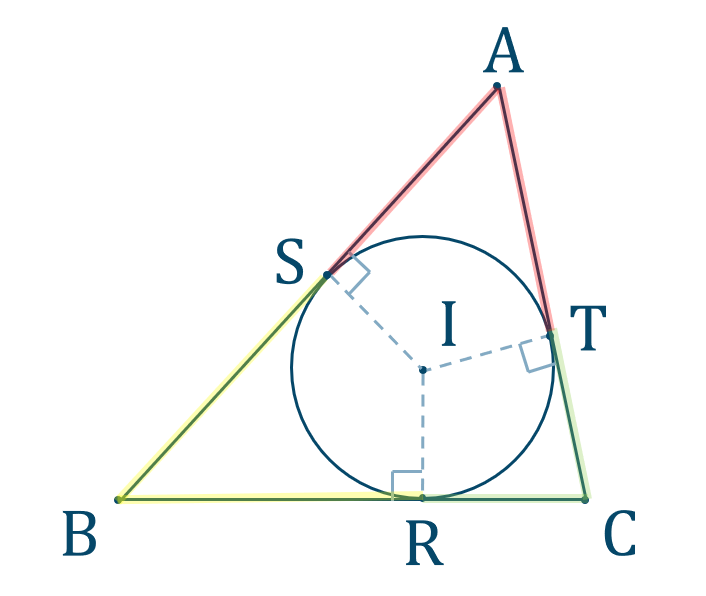
Point：三角形の内心【定理】三角形の３つの内角の二等分線は１点で交わる。

このとき、交点 ${\rm I}$ を中心とすれ円を $\triangle {\rm ABC}$ の内接円といい、点 ${\rm I}$ を内心という。

・内心についての性質
( ⅰ ) 角の二等分線
頂点から内心 ${\rm I}$ に引いた線は角の二等分線となるので、

$$\angle{\rm BAI}=\angle{\rm CAI}$$

が成り立ちます。また、他の頂点でも同様に成り立ちます。

( ⅱ ) 円と接線の性質
図のように接点を ${\rm S},{\rm T}$ とすると、

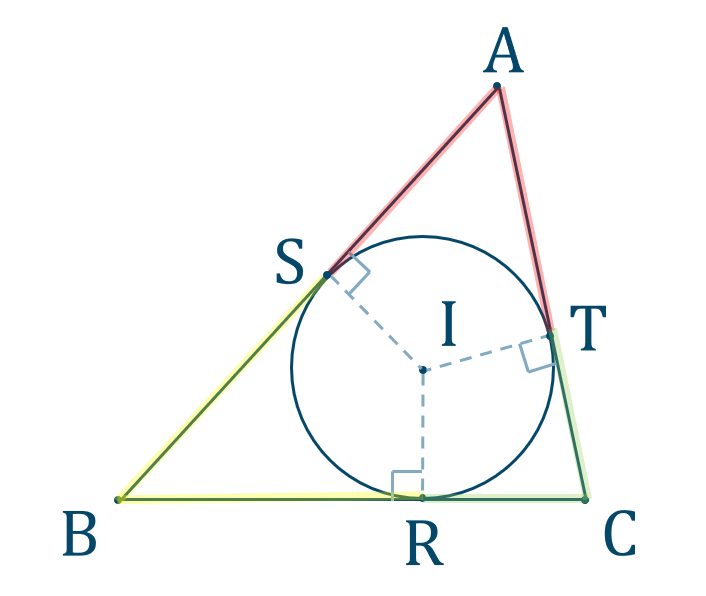
円と接線の性質より、

$${\rm AS}={\rm AT}$$$$~~~\angle{\rm ISA}=\angle{\rm ITA}=90^\circ$$

が成り立ちます。また、他の頂点でも同様に成り立ちます。

問題と詳しい解説はこちらから

三角形の内心

三角形の五心の１つである内心について解説していきます。内接円の性質についてもあわせて覚えておきましょう。

三角形の垂心

Point：三角形の垂心【定理】三角形の３つの頂点から対辺に下ろした垂線は１点で交わる。

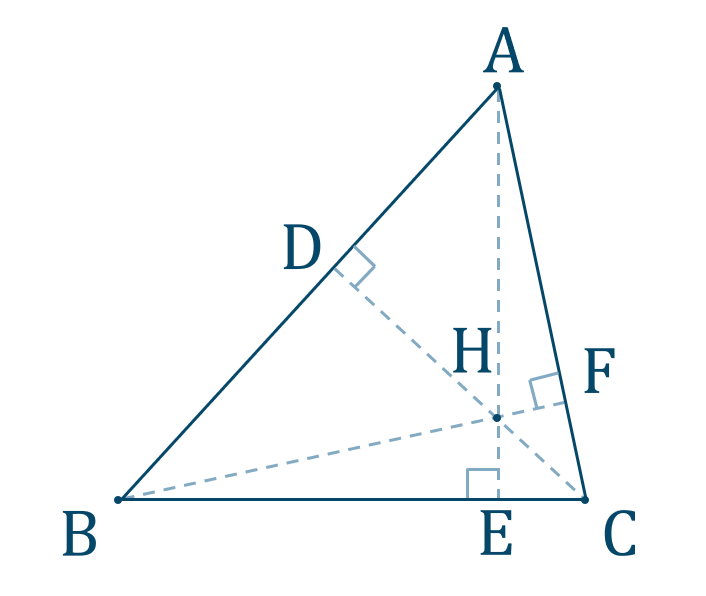
このとき、交点 ${\rm H}$ を三角形の垂心といいます。
また、垂線を３本引くので $\triangle {\rm ABC}$ の内部で複数の直角三角形ができます。これらを用いて問題を解きましょう。

問題と詳しい解説はこちらから

三角形の垂心

三角形の五心の１つである垂心について解説していきます。直角になる位置を確認し、直角三角形の内角の和を利用して解いていきましょう。

三角形の重心

Point：三角形の重心【定理】３つの頂点とその対辺の中点を結ぶ線を中線といい、この３つの中線は１点で交わりその各中線を $2:1$ に内分する。

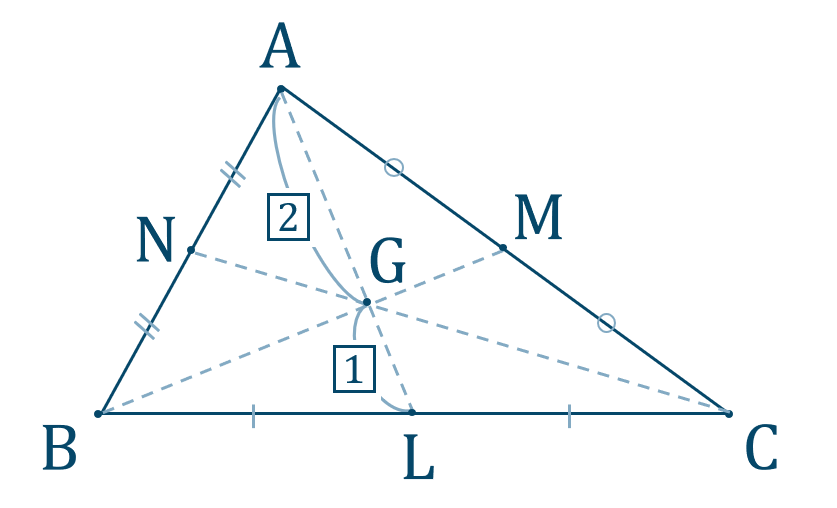
このときの交点 ${\rm G}$ を三角形の重心といいます。
${\rm L}$ $,$ ${\rm M}$ $,$ ${\rm N}$ を各辺の中点とすると、

$$~{\rm AN}:{\rm NB}={\rm BL}:{\rm LC}={\rm AM}:{\rm MC}$$$$=1:1$$

また、定理より、

$$~{\rm AG}:{\rm GL}={\rm BG}:{\rm GM}={\rm CG}:{\rm GN}$$$$=2:1$$

問題と詳しい解説はこちらから

三角形の重心

三角形の五心の１つである重心について解説していきます。重心の位置と中点を $2:1$ に内分することを利用して解きましょう。

チェバの定理

Point：チェバの定理解法の手順は、
① 着目する三角形を決めます。
次の図の $\triangle {\rm ABC}$ に着目する。

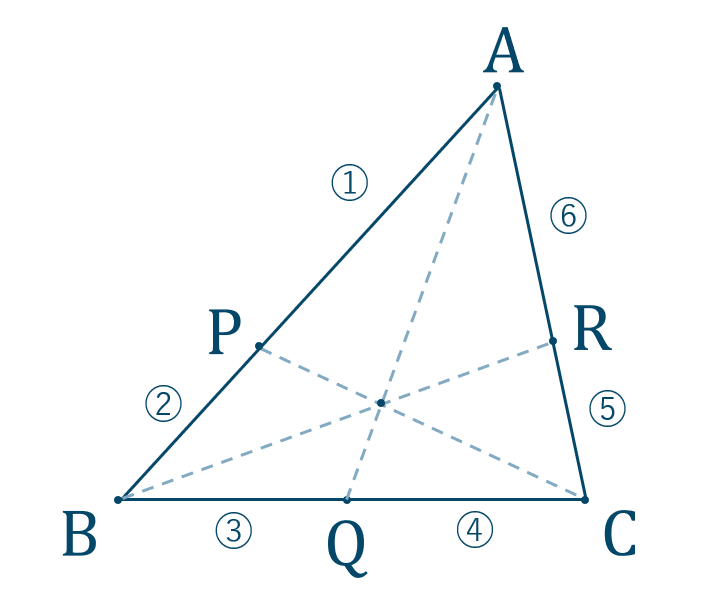
② 頂点 ${\rm A}$ $,$ ${\rm B}$ $,$ ${\rm C}$ と交点 ${\rm P}$ $,$ ${\rm Q}$ $,$ ${\rm R}$ を確認して、頂点→交点→頂点→…と進んでいくルートを決めます。$$~~~{\rm A}~\to~{\rm P}~\to~{\rm B}~\to~{\rm Q}~\to~{\rm C}~\to~{\rm R}~\to~{\rm A}$$③ チェバの定理より式を立てます。

$$\frac{{\rm AP}}{{\rm PB}}\times \frac{{\rm BQ}}{{\rm QC}}\times \frac{{\rm CR}}{{\rm RA}}=1$$

問題と詳しい解説はこちらから

チェバの定理

今回はチェバの定理について解説していきます。公式をそのまま覚えるのではなく、立式の仕方をおさえておきましょう。

メネラウスの定理

Point：メネラウスの定理解法の手順は、
① 着目する三角形を決めます。
次の図の $\triangle {\rm ABC}$ に着目する。

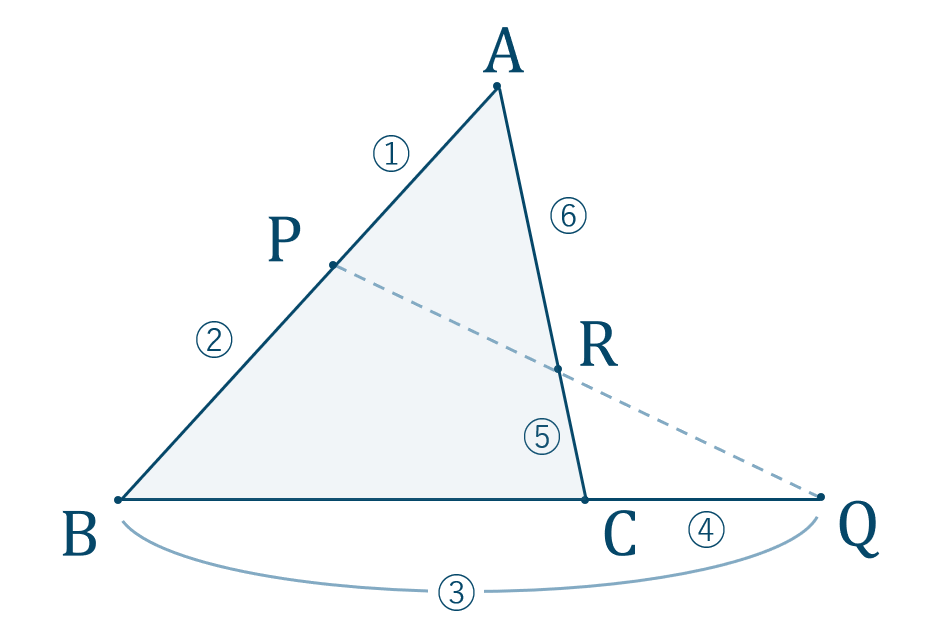
ここで着目する三角形が変わると、違う式が得られます。
② 頂点 ${\rm A}$ $,$ ${\rm B}$ $,$ ${\rm C}$ と交点 ${\rm P}$ $,$ ${\rm Q}$ $,$ ${\rm R}$ を確認して、頂点→交点→頂点→…と進んでいくルートを決めます。$$~~~{\rm A}~\to~{\rm P}~\to~{\rm B}~\to~{\rm Q}~\to~{\rm C}~\to~{\rm R}~\to~{\rm A}$$③ メネラウスの定理より式を立てます。

$$\frac{{\rm AP}}{{\rm PB}}\times \frac{{\rm BQ}}{{\rm QC}}\times \frac{{\rm CR}}{{\rm RA}}=1$$

① 着目する三角形を $\triangle {\rm PBQ}$ とする。
② 頂点 ${\rm P}$ $,$ ${\rm B}$ $,$ ${\rm Q}$ と交点 ${\rm A}$ $,$ ${\rm R}$ $,$ ${\rm C}$ を確認して、頂点→交点→頂点→…と進んでいくルートを決めます。$$~~~{\rm P}~\to~{\rm A}~\to~{\rm B}~\to~{\rm C}~\to~{\rm Q}~\to~{\rm R}~\to~{\rm P}$$③ メネラウスの定理より式を立てます。

$$\frac{{\rm PA}}{{\rm AB}}\times \frac{{\rm BC}}{{\rm CQ}}\times \frac{{\rm QR}}{{\rm RP}}=1$$

問題と詳しい解説はこちらから

メネラウスの定理

今回はメネラウスの定理について解説していきます。チェバの定理と同様に着目する三角形を決めて考えましょう。

三角形の辺と角の大小関係

Point：三角形の辺と角の大小関係【定理】
① 大きい辺に向かい合う角は、小さい辺に向かい合う角より大きい。
② 大きい角に向かい合う辺は、小さい角に向かい合う辺より大きい。

これらをまとめると、三角形の辺とそれに対する角の大小関係は一致します。
例えば、

$${\small\angle}{\rm A}>{\small\angle}{\rm B}>{\small\angle}{\rm C}~\Leftrightarrow~a>b>c$$

問題と詳しい解説はこちらから

三角形の辺と角の大小関係

今回は三角形の辺と角の大小関係について解説していきます。最大辺と最大角の対応をおさえておきましょう。

三角形になるための条件

Point：三角形になるための条件三角形の３辺 $a~,~b~,~c$ について、
２辺の和が他の１辺より大きくなるので、

$$\begin{eqnarray} a+b>c \\ b+c>a \\ c+a>b \end{eqnarray}$$

これらがすべて成り立ちます。

逆に、３つの値が３辺の長さとなる三角形となるためには、上のの３つの式がすべて成り立つ必要があります。

問題と詳しい解説はこちらから

三角形になるための条件

今回は与えれれた３つの辺で三角形がつくれるかどうかの問題を解説していきます。３つの辺より３つの条件式を作りましょう。

円周角と中心角

Point：円周角と中心角(1) 弧の長さが等しい$~\Leftrightarrow~$円周角が等しい

上の図で弧 ${\rm AB}$ と弧 ${\rm CD}$ が等しいとき、

$$\angle{\rm APB}=\angle{\rm AQB}=\angle{\rm CRD}$$

(2) 円周角は中心角の半分である

上の図で、

$$\angle{\rm AOB}=2\angle{\rm APB}$$

(3) 弧の長さが等しい $~\Leftrightarrow~$ 中心角が等しい

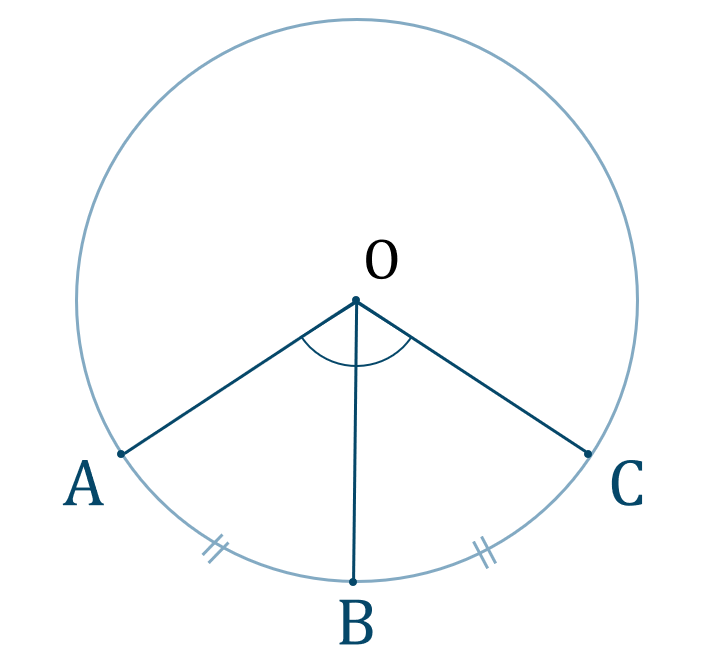
上の図で弧 ${\rm AB}$ と弧 ${\rm CD}$ が等しいとき、

$$\angle{\rm AOB}=\angle{\rm BOC}$$

また、

$$\angle{\rm AOC}=2\angle{\rm AOB}$$

これより、弧の長さの比と中心角の比は一致します。

問題と詳しい解説はこちらから

円周角と中心角

今回は円周角と中心角について解説していきます。通常の円周角と中心角の関係だけでなく、弧の長さの比と円周角の値についてもおさえておきましょう。

円に内接する四角形と角

Point：円に内接する四角形と角四角形が円に内接するとき、
四角形の対角の和は $180^\circ$ となります。

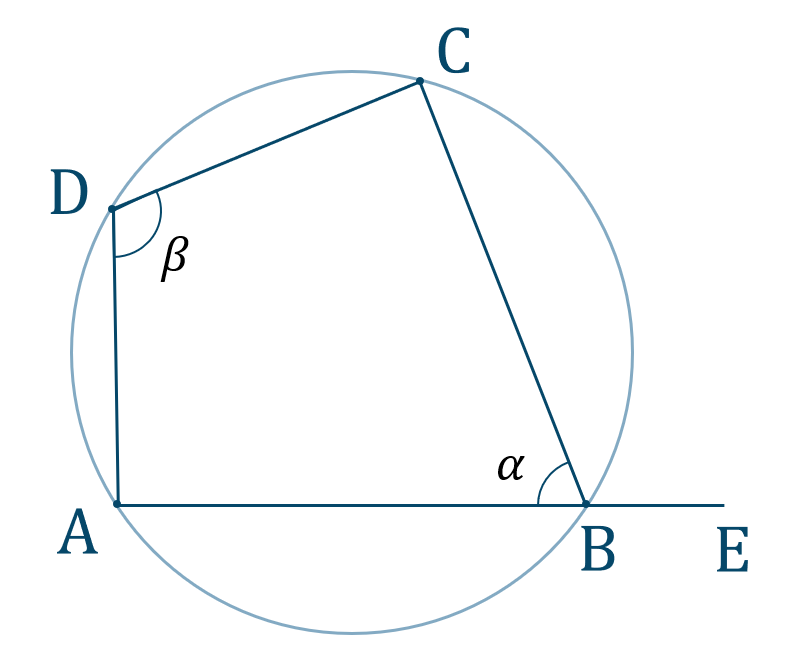
上の図より、

$$\alpha+\beta=180^\circ$$

逆に、四角形の対角が等しければその四角形は円に内接します。

問題と詳しい解説はこちらから

円に内接する四角形と角

今回は円に内接する四角形の角の条件について解説していきます。対角の和が 180° になる条件と、それを用いて円に内接することを示す問題を見ていきましょう。

接弦定理

Point：接弦定理

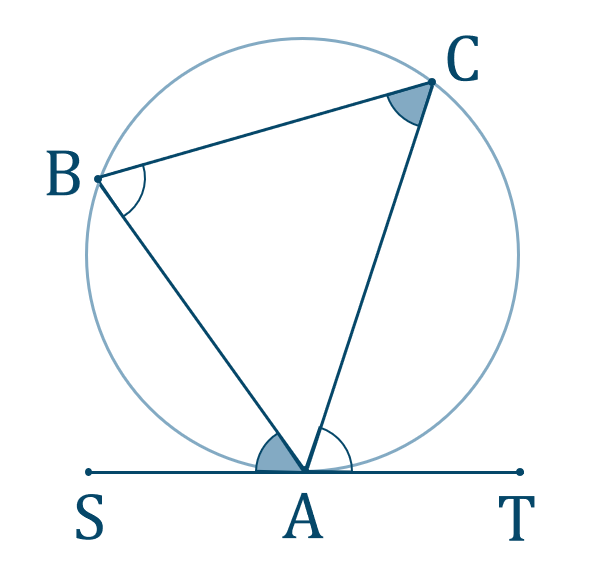
上の図で、$\triangle {\rm ABC}$ の外接円と点 ${\rm A}$ での接線 ${\rm ST}$ において、

$$\angle{\rm CAT}=\angle{\rm ABC}$$

また、

$$\angle{\rm BAS}=\angle{\rm BCA}$$

これらが成り立ちます。

問題と詳しい解説はこちらから

接弦定理

角の値の定理である接弦定理について解説していきます。三角形と内接円、その頂点での接線があるときこの定理を用いて解いていきましょう。

内接円と接線の条件

Point：内接円と接線の条件三角形とその内接円について、図のように接点を ${\rm S},{\rm T}$ とすると、

円と接線の性質より、

$${\rm AS}={\rm AT}$$$$\angle{\rm ISA}=\angle{\rm ITA}=90^\circ$$

が成り立ちます。また、他の頂点でも同様に成り立ちます。

また、次のように $\angle{\rm SAT}=90^\circ$ であるとき、

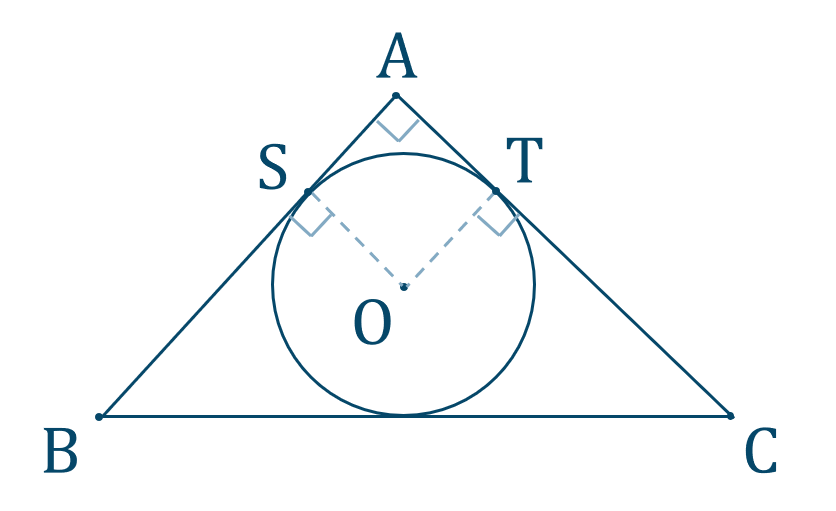
円より、四角形 ${\rm ASOT}$ は正方形となります。よって、

$${\rm AS}={\rm AT}={\rm OS}={\rm OT}$$

となり、円の半径と等しくなります。

問題と詳しい解説はこちらから

内接円と接線の条件

内接円と接線の条件を用いる問題について解説していきます。どの線分が等しくなっていくかを確認していきましょう。

方べきの定理

Point：方べきの定理解法の手順は、
① ２本の直線のそれぞれについて、「円上の点→交点」と進む積の値を求めます。

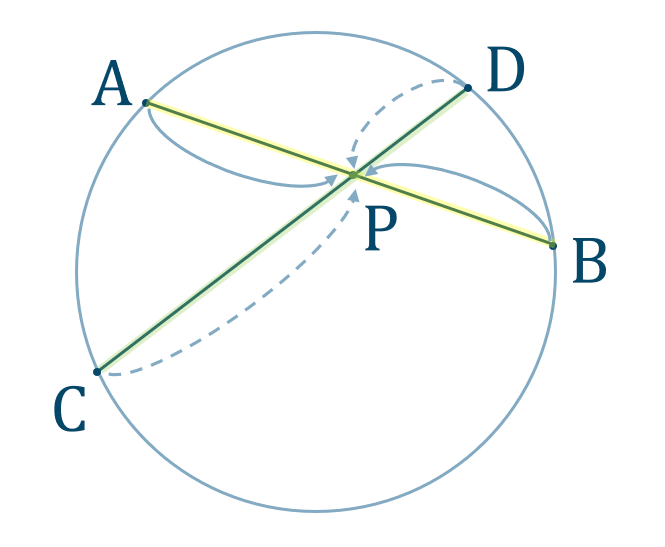
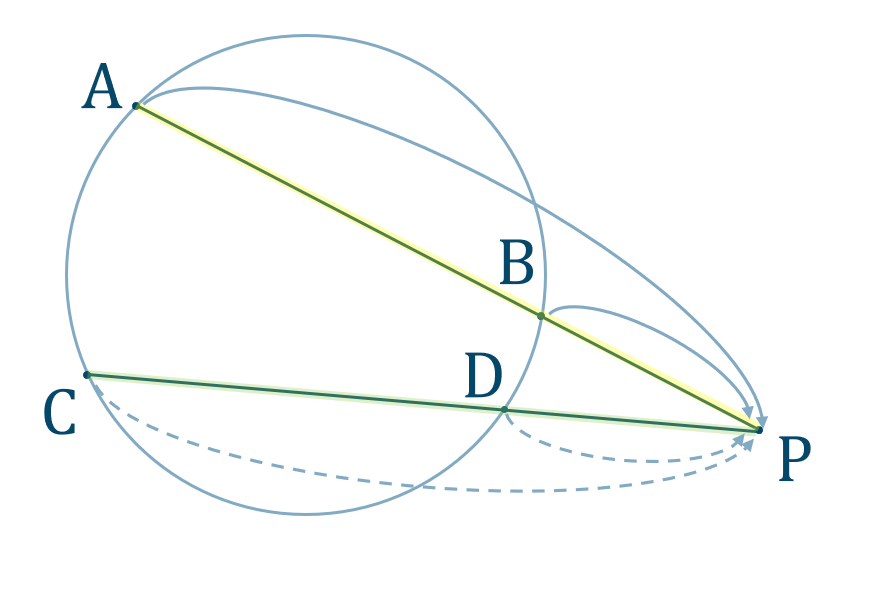
② 上で求めた値をイコールで結びます。

$${\rm AP}\times{\rm BP}={\rm CP}\times{\rm DP}$$

また、接線がある場合は
片方の直線を「(接線の長さ)²」として計算します。

$${\rm AP}\times{\rm BP}={\rm TP}^2$$

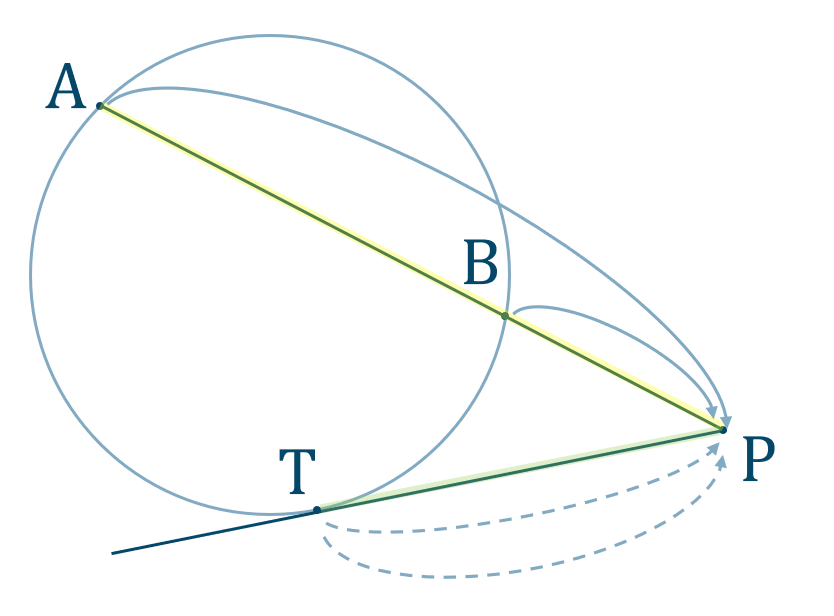
（※教科書の表記と異なる場合があります。）

問題と詳しい解説はこちらから

方べきの定理

今回は方べきの定理について解説していきます。公式をそのまま覚えていても解けない事があるので、その使い方もあわせて覚えておきましょう。

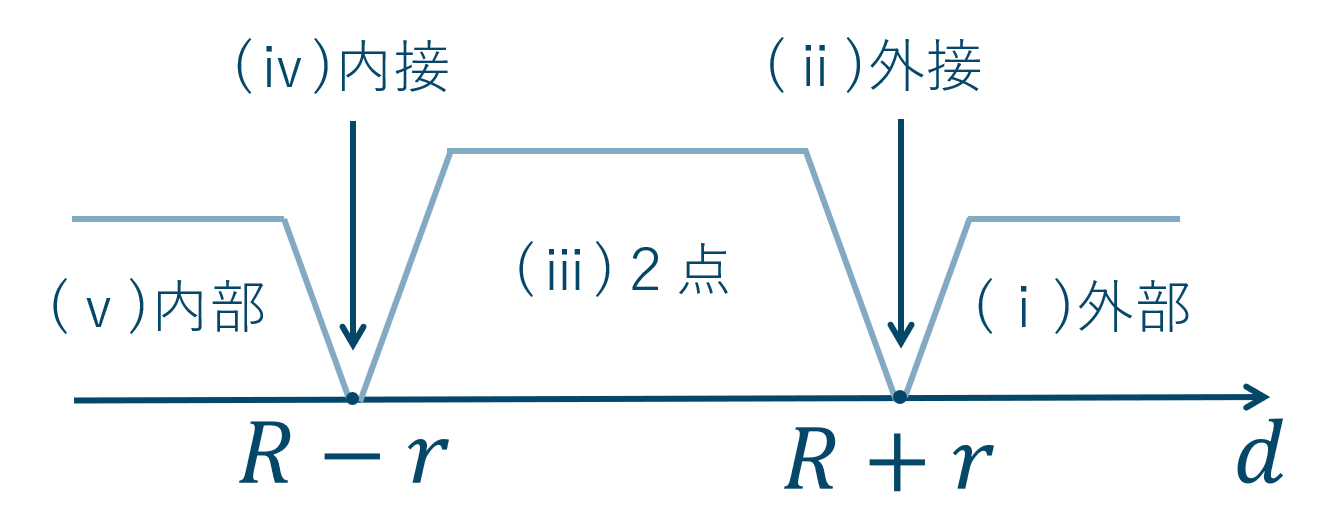
２つの円の位置関係と共通接線

Point：タイトル２つの円 $C_1~,~C_2$ の半径がそれぞれ $R~,~r$ （ただし、$R>r$ ）となり、２つの円の中心間の距離を $d$ とするとき、
$d$ と $R+r$ と $R-r$ の大小関係より、２つの円の位置関係の条件を求めます。

( ⅰ ) $d>R+r$ のとき

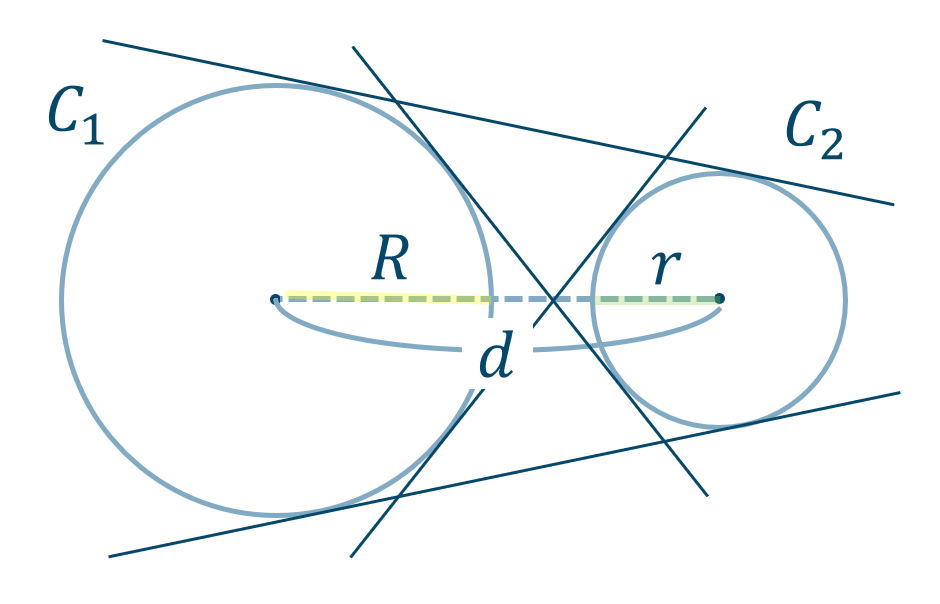
２つの円は離れている（外部にある）
共通接線は４本

( ⅱ ) $d=R+r$ のとき

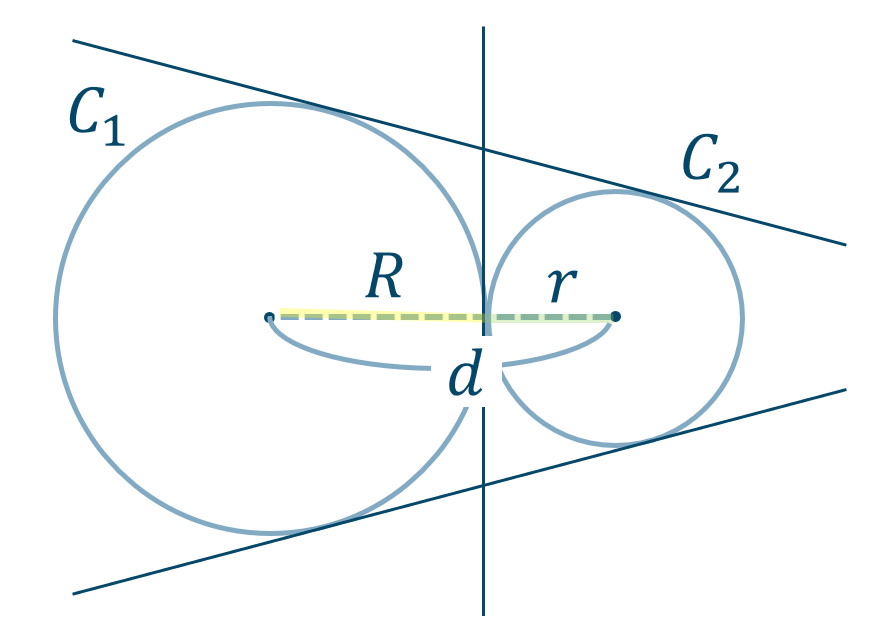
２つの円は互いに外接する
共通接線は３本

( ⅲ ) $R-r<d<R+r$ のとき

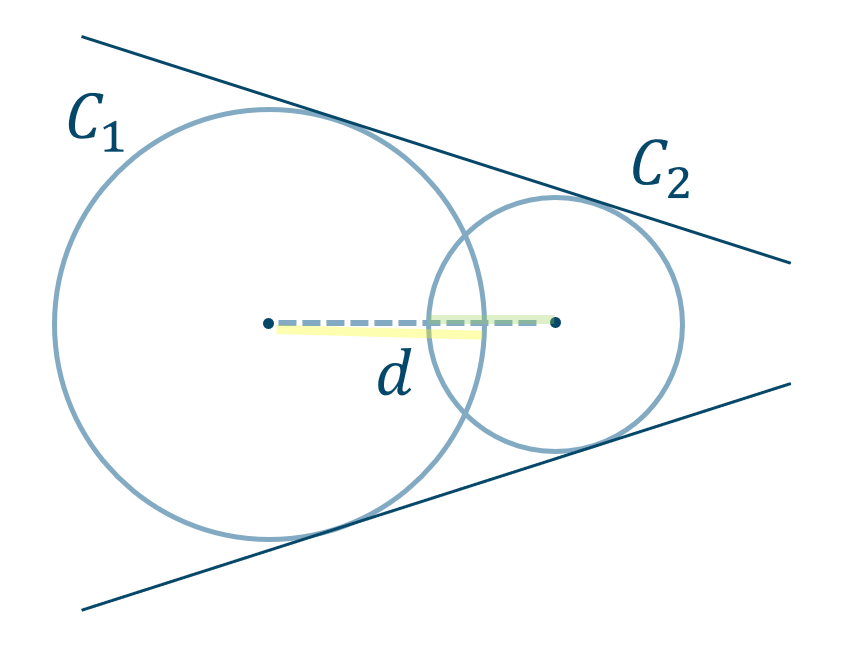
２つの円は２点で交わる
共通接線は２本

( ⅳ ) $d=R-r$ のとき

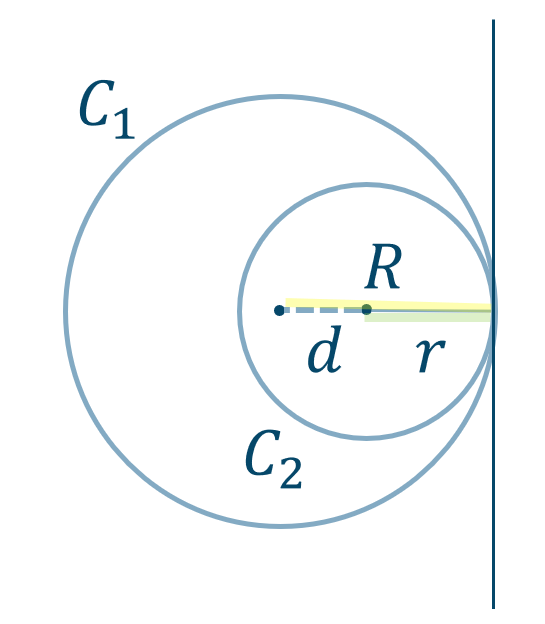
円 $C_2$ が円 $C_1$ に内接する
共通接線は１本

( ⅴ ) $d<R-r$ のとき

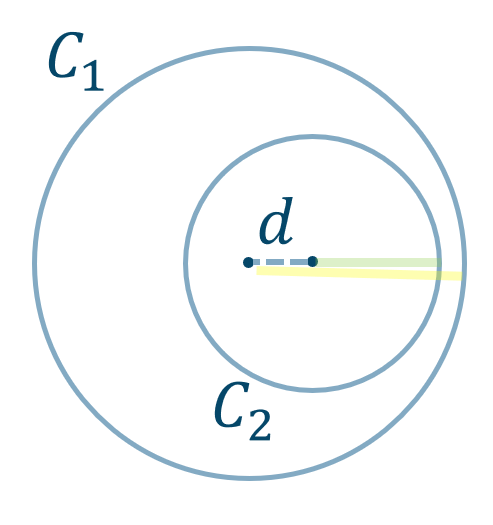
円 $C_2$ が円 $C_1$ の内部にある
共通接線は０本

問題と詳しい解説はこちらから

２つの円の位置関係と共通接線

２つの円の位置関係と共通接線の本数について解説していきます。位置関係については２つの円の半径の和と差を計算し、中心間の距離と比較して調べましょう。

共通接線の長さ

Point：共通接線の長さパターン(1)

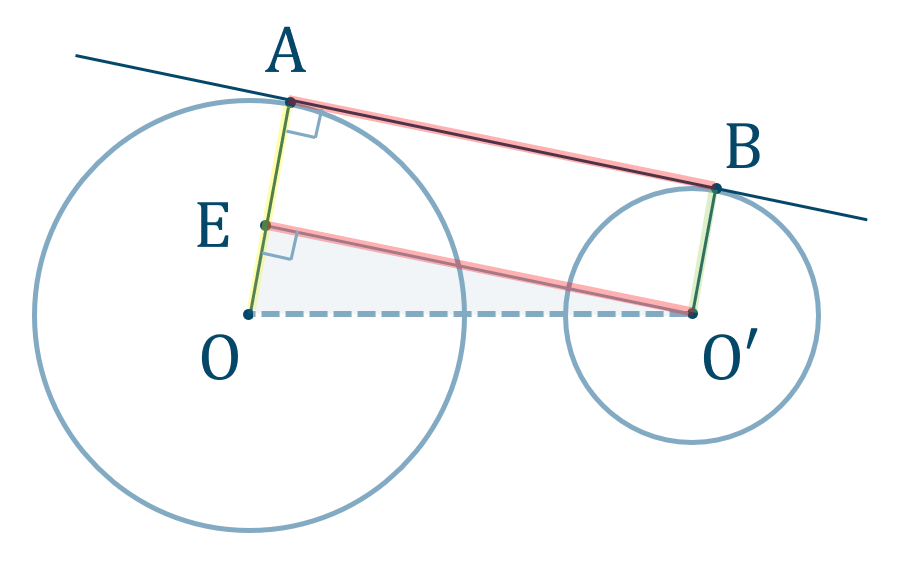
${\rm AB}$ を平行移動して、$\triangle {\rm OO’E}$ で三平方の定理を用いる。

パターン(2)

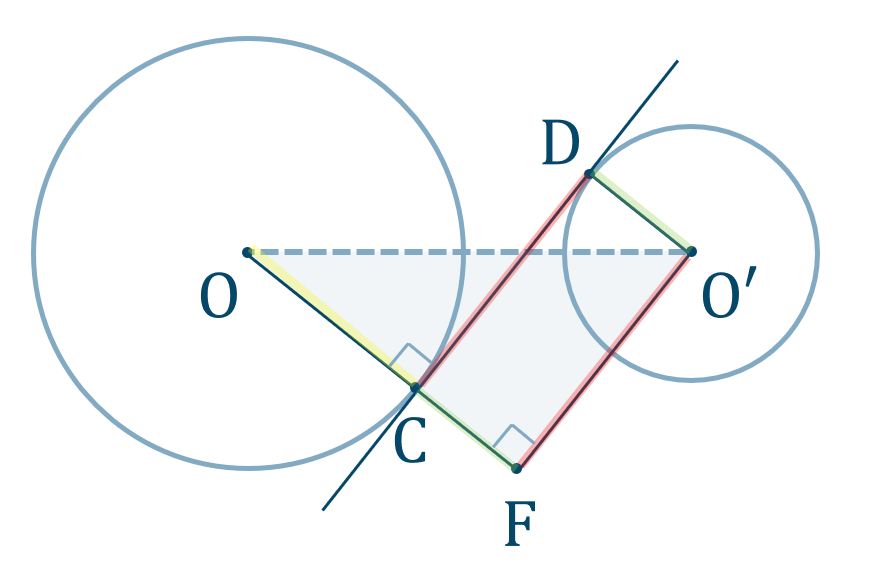
${\rm CD}$ を平行移動して、$\triangle {\rm OO’F}$ で三平方の定理を用いる。

問題と詳しい解説はこちらから

共通接線の長さ

今回は共通接線を用いた計算問題について解説していきます。共通接線の線分を平行移動して三平方の定理を用いることを覚えておきましょう。

【問題一覧】数学Ａ：図形の性質

このページは「高校数学Ａ：図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないとき...