今回の問題は「三角形の重心」です。
問題次の図で、\(\triangle {\rm ABC}\) の重心を \({\rm G}\)、直線 \({\rm AG}\) と直線 \({\rm BC}\) との交点を \({\rm D}\) とするとき、次の比の値を求めよ。$$~~~\triangle {\rm ABC}:\triangle {\rm ABD}:\triangle {\rm ABG}:\triangle {\rm GBD}$$
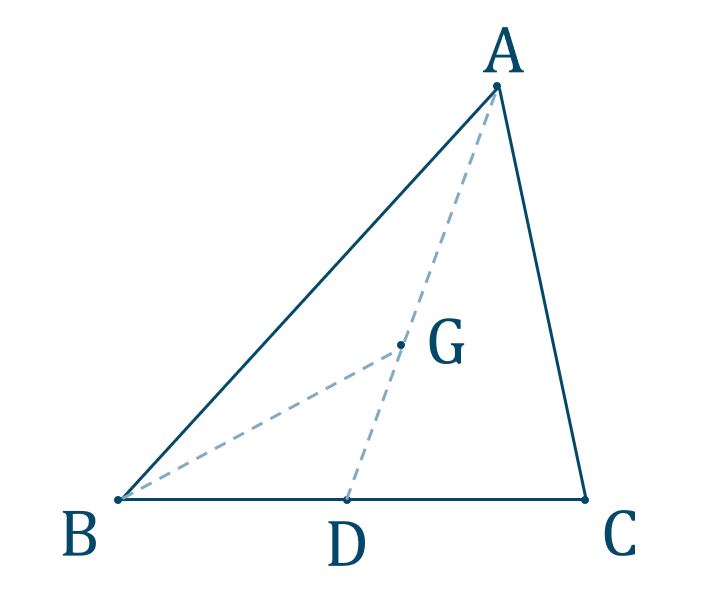
次のページ「解法のPointと問題解説」


