今回の問題は「三角形の内心」です。
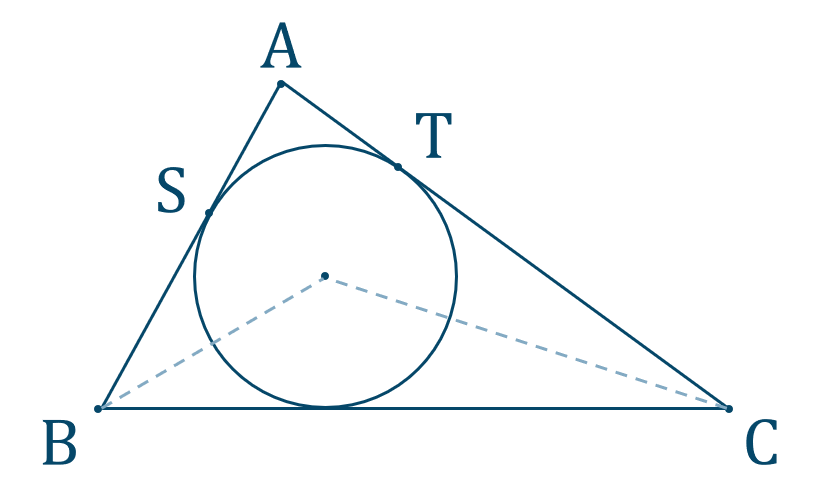
問題次の図で \(\triangle {\rm ABC}\) とその内心 \({\rm I}\) について、この内接円の直線 \({\rm AB}\) との接点を \({\rm S}\)、直線 \({\rm AC}\) との接点を \({\rm T}\) として、\(\angle{\rm A}=80^\circ\) のとき、次の角を求めよ。
 $${\small (1)}~\angle{\rm BIC}$$$${\small (2)}~\angle{\rm AST}$$$${\small (3)}~\angle{\rm SIT}$$
$${\small (1)}~\angle{\rm BIC}$$$${\small (2)}~\angle{\rm AST}$$$${\small (3)}~\angle{\rm SIT}$$
 $${\small (1)}~\angle{\rm BIC}$$$${\small (2)}~\angle{\rm AST}$$$${\small (3)}~\angle{\rm SIT}$$
$${\small (1)}~\angle{\rm BIC}$$$${\small (2)}~\angle{\rm AST}$$$${\small (3)}~\angle{\rm SIT}$$
次のページ「解法のPointと問題解説」


