今回の問題は「円周角と中心角」です。
問題次の問いに答えよ。
\({\small (1)}\) 次の図の角度 \(x~,~y\) の値を求めよ。
\({\large ①}\)

\({\large ②}\)

\({\large ③}\)

\({\small (2)}\) 円 \({\rm O}\) の円上に3点 \({\rm A}\) \(,\) \({\rm B}\) \(,\) \({\rm C}\) をとり、次の比が成り立つとき、$$~~~{\rm AB}:{\rm BC}:{\rm CA}=3:4:5$$\(\angle{\rm ACB}\) \(,\) \(\angle{\rm BAC}\) \(,\) \(\angle{\rm ABC}\) の値を求めよ。
\({\small (1)}\) 次の図の角度 \(x~,~y\) の値を求めよ。
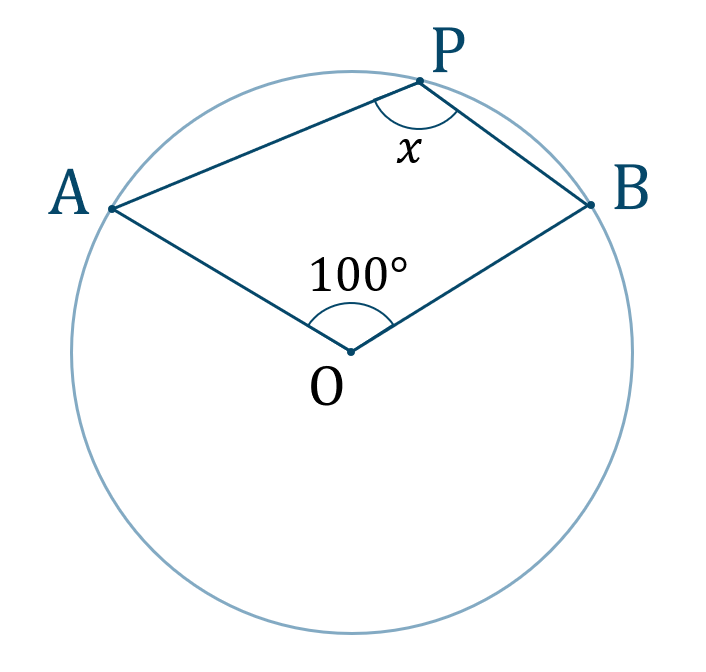
\({\large ①}\)
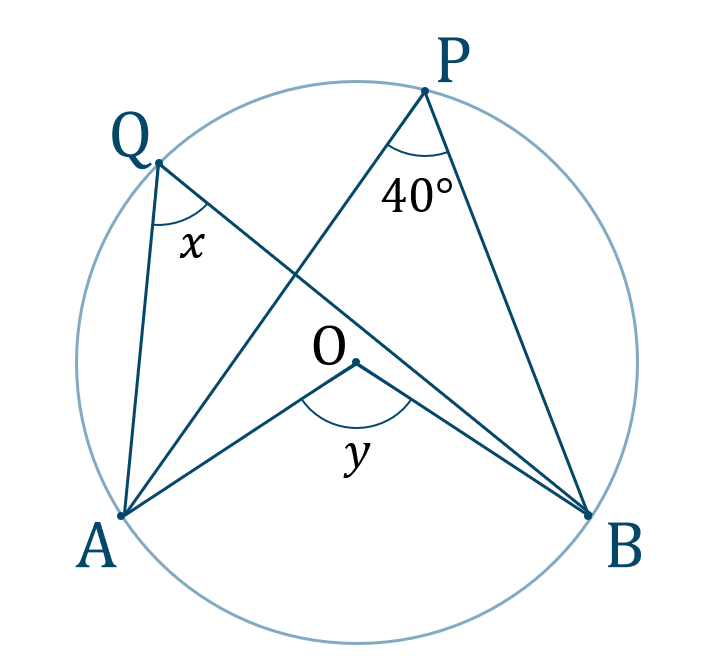
\({\large ②}\)
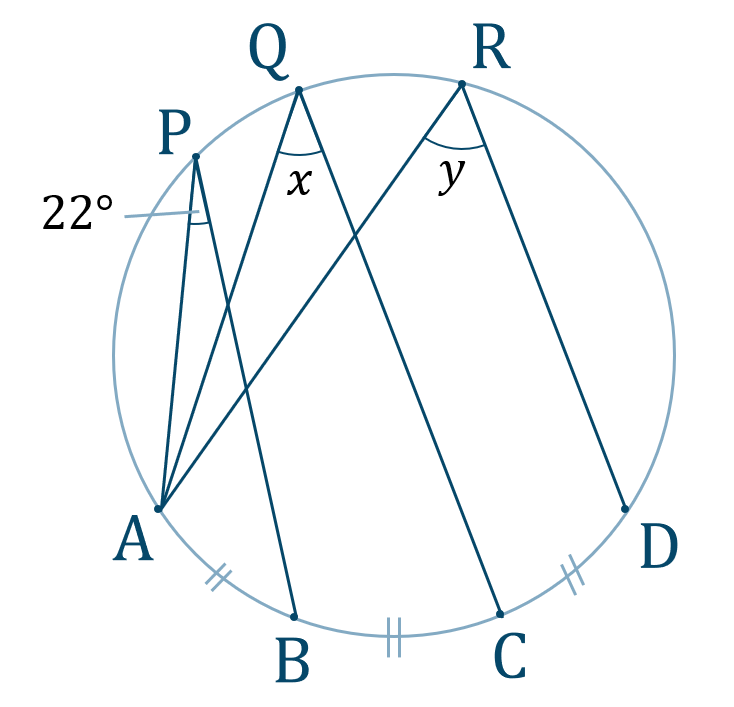
\({\large ③}\)
\({\small (2)}\) 円 \({\rm O}\) の円上に3点 \({\rm A}\) \(,\) \({\rm B}\) \(,\) \({\rm C}\) をとり、次の比が成り立つとき、$$~~~{\rm AB}:{\rm BC}:{\rm CA}=3:4:5$$\(\angle{\rm ACB}\) \(,\) \(\angle{\rm BAC}\) \(,\) \(\angle{\rm ABC}\) の値を求めよ。
次のページ「解法のPointと問題解説」


