今回の問題は「2次不等式の文章問題」です。
問題次の図のように、縦 \(6~m\) 、横 \(8~m\) の土地の周りに幅が一定の道を作る。

このとき、道を含めた全体の面積が \(80~m^2\) 以上 \(168~m^2\) 以下になるためには道の幅を何 \(m\) の範囲にすればよいか答えよ。
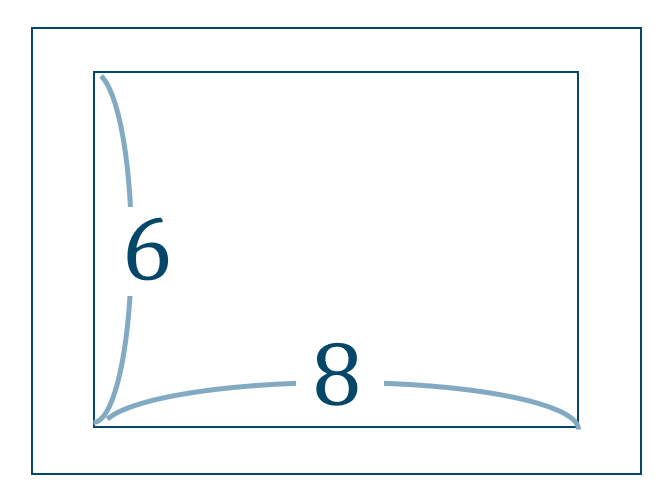
このとき、道を含めた全体の面積が \(80~m^2\) 以上 \(168~m^2\) 以下になるためには道の幅を何 \(m\) の範囲にすればよいか答えよ。
次のページ「解法のPointと問題解説」