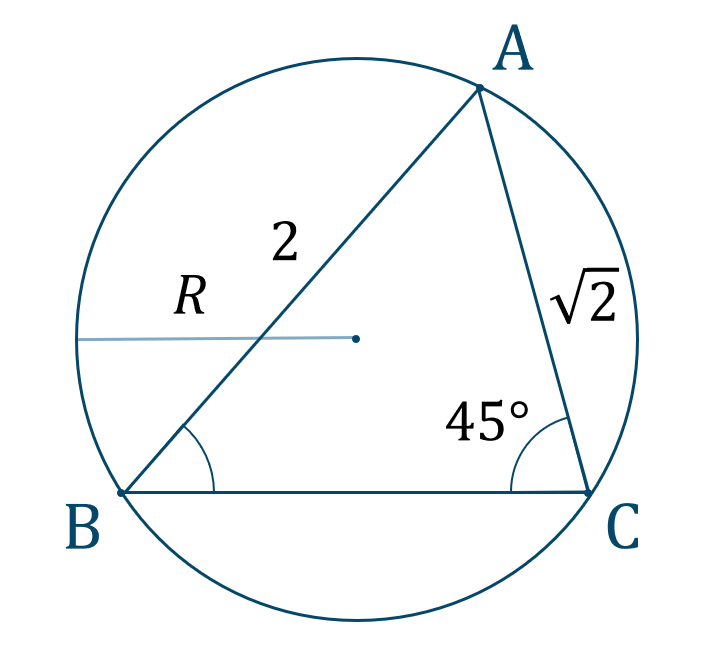正弦定理の解法
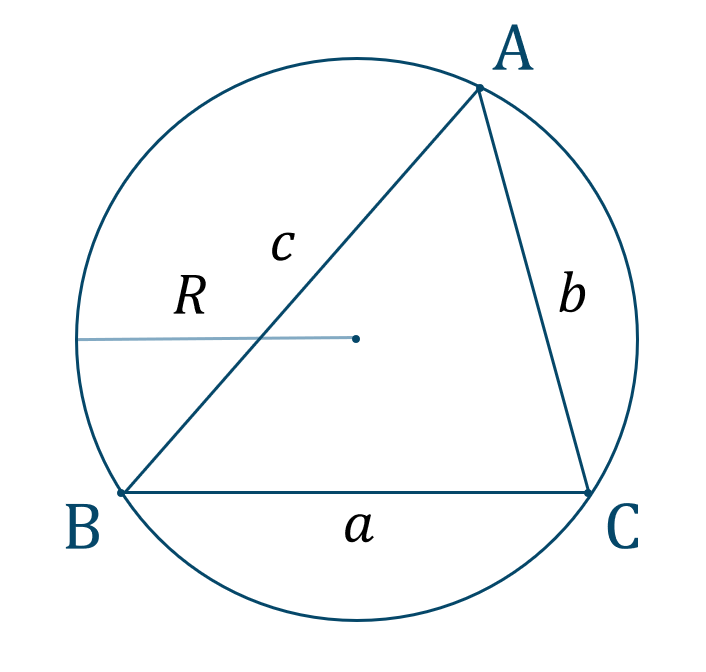
正弦定理は、
このままでは公式が使いにくいので、
( ⅰ ) 2組の辺と角が条件のとき
辺角辺角のうち1つがわかっていないときは、2組の辺とと正弦の値の比が一定であることより、
計算はななめ掛けをして、
として計算しましょう。
( ⅱ ) 外接円の半径を求めるとき、
1組の辺と角より、
これを用いて計算しましょう。
問題解説:正弦定理
問題解説(1)
与えられた図形は次のようになります。
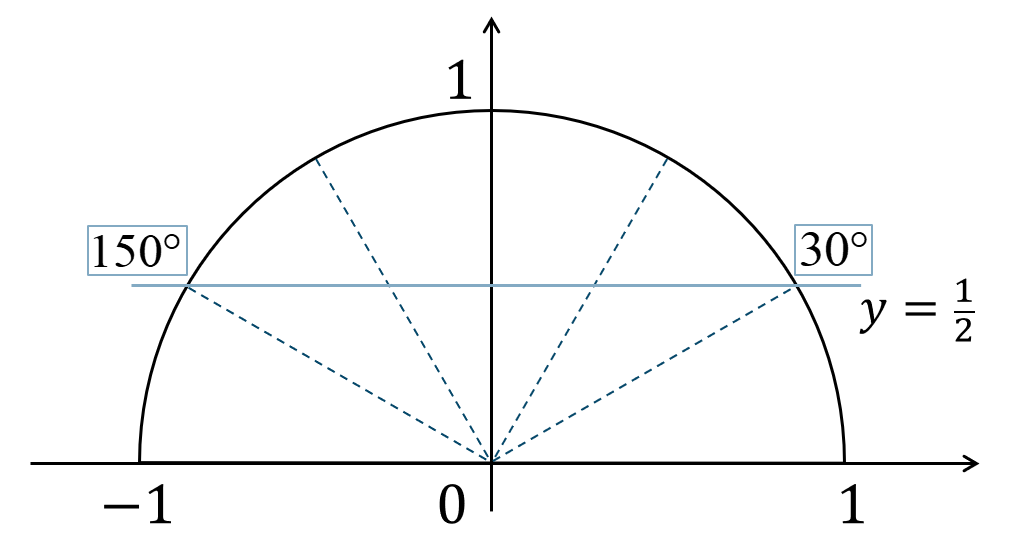
\(\angle{\rm C}\) と \(\angle{\rm B}\) について正弦定理を用いると、$$\hspace{ 10 pt}\frac{2}{\sin{45^\circ}}=\frac{\sqrt{2}}{\sin{{\rm B}}}$$ななめ掛けすると、$$\hspace{ 10 pt}2\sin{{\rm B}}=\sqrt{2}\sin{45^\circ}$$計算すると、$$\hspace{ 10 pt}2\sin{{\rm B}}=\sqrt{2}\cdot\frac{1}{\sqrt{2}}$$$$\hspace{ 10 pt}2\sin{{\rm B}}=1$$両辺を \(2\) で割ると、$$\hspace{ 10 pt}\sin{{\rm B}}=\frac{1}{2}$$単位円上に表すと、
よって、$$~~~\angle{\rm B}=30^\circ~,~150^\circ$$ここで、\(150^\circ\) のときは三角形とならないので不適となります。
よって、答えは$$~~~\angle{\rm B}=30^\circ$$となります。
問題解説(2)
三角形の内角の和が \(180^\circ\) より、$$\hspace{ 10 pt}\angle{\rm A}+\angle{\rm B}+\angle{\rm C}=180^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm A}=180^\circ-(\angle{\rm B}+\angle{\rm C})$$値を代入すると、$$\hspace{ 10 pt}\angle{\rm A}=180^\circ-(30^\circ+45^\circ)$$$$\hspace{ 28 pt}=180^\circ-75^\circ$$$$\hspace{ 28 pt}=105^\circ$$よって、答えは$$~~~\angle{\rm A}=105^\circ$$となります。
問題解説(3)
220より、$$\hspace{ 10 pt}2R=\frac{c}{\sin{{\rm C}}}$$値を代入すると、$$\hspace{ 10 pt}2R=\frac{2}{\sin{45^\circ}}$$$$\hspace{ 10 pt}2R=\frac{2}{{\large \frac{1}{\sqrt{2}}}}$$分母分子に \(\sqrt{2}\) をかけると、$$\hspace{ 10 pt}2R=\frac{2\times\sqrt{2}}{{\large \frac{1}{\sqrt{2}}}\times\sqrt{2}}$$$$\hspace{ 10 pt}2R=2\sqrt{2}$$両辺を \(\sqrt{2}\) で割ると、$$\hspace{ 10 pt}R=\sqrt{2}$$よって、答えは$$~~~R=\sqrt{2}$$となります。
今回のまとめ
正弦定理の公式を使うときは、着目する2組の辺と角を決めましょう。また、外接円の半径を求めるときにも、正弦定理を使います。