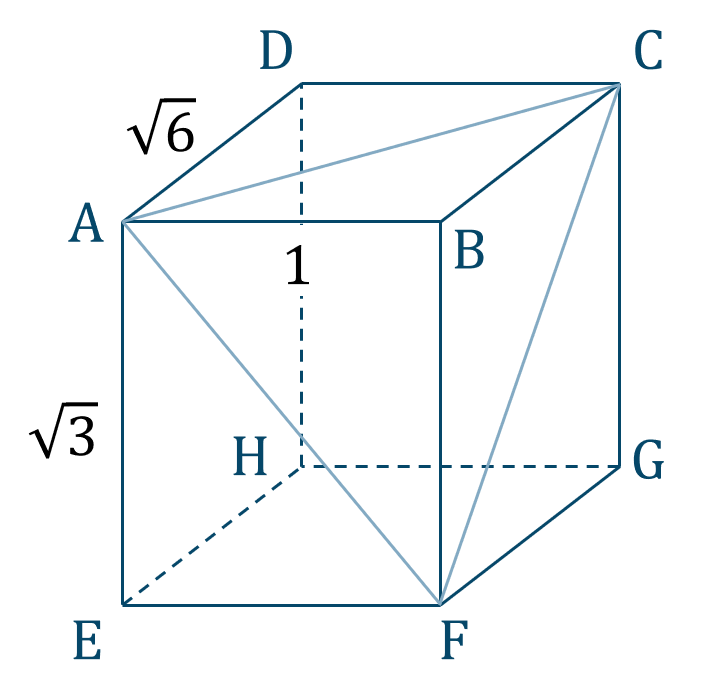
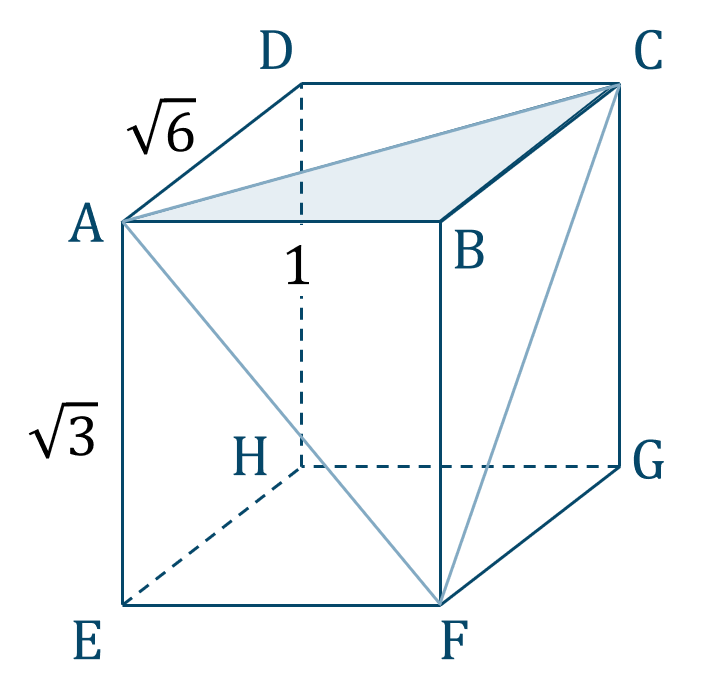
直方体の計量
「必要な部分を平面図形として抜き出して考える」
これが重要となります。
直方体の内部の三角錐の体積は、２通りの方法で求めることができます。
上の直方体について、三角錐 \({\rm BAFC}\) の体積 \(V\) は、
( ⅰ ) \(\triangle {\rm ABC}\) を底面とすると、
( ⅱ ) \(\triangle {\rm AFC}\) を底面とすると、
点 \({\rm B}\) から \(\triangle {\rm AFC}\) に下ろした垂線を \({\rm BI}\) とすると、
この２通りを用いて計算しましょう。
問題解説:直方体の計量
問題解説(1)
与えられた図形は次のようになります。
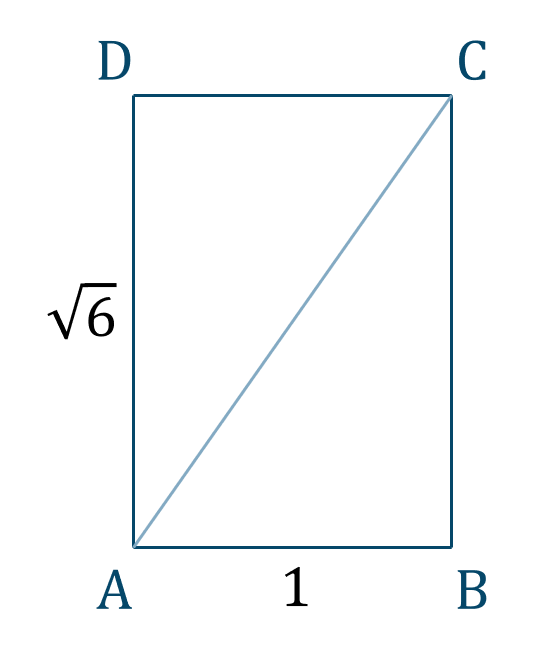
ここで長方形 \({\rm DABC}\) を考えると、
これより、三平方の定理を用いると、$$\hspace{ 10 pt}{\rm AC}^2=(\sqrt{6})^2+1^2$$$$\hspace{ 31 pt}=6+1$$$$\hspace{ 31 pt}=7$$ここで、\({\rm AC}>0\) より、$$\hspace{ 10 pt}{\rm AC}=\sqrt{7}~~\cdots{\large ①}$$
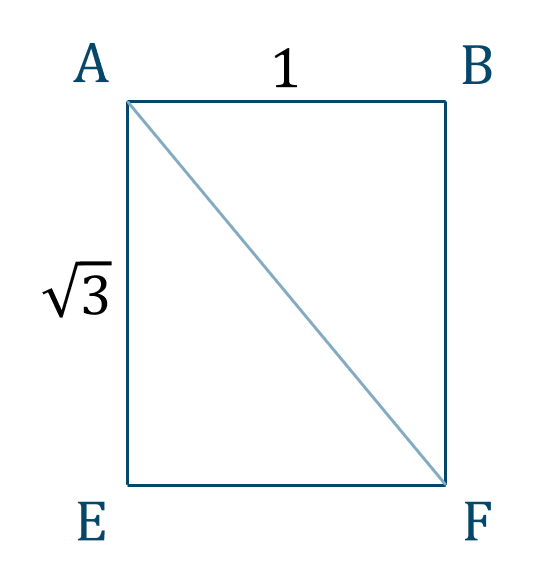
次に長方形 \({\rm AEFB}\) を考えると、
これより、三平方の定理を用いると、$$\hspace{ 10 pt}{\rm AF}^2=(\sqrt{3})^2+1^2$$$$\hspace{ 31 pt}=3+1$$$$\hspace{ 31 pt}=4$$ここで、\({\rm AF}>0\) より、$$\hspace{ 10 pt}{\rm AF}=2~~\cdots{\large ②}$$
次に長方形 \({\rm BFGC}\) を考えると、
これより、三平方の定理を用いると、$$\hspace{ 10 pt}{\rm CF}^2=(\sqrt{3})^2+(\sqrt{6})^2$$$$\hspace{ 30 pt}=3+16$$$$\hspace{ 30 pt}=9$$ここで、\({\rm CF}>0\) より、$$\hspace{ 10 pt}{\rm CF}=3~~\cdots{\large ③}$$
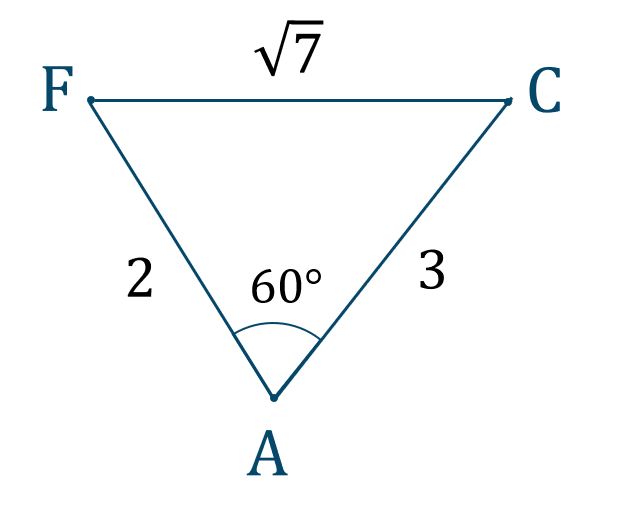
次に \(\triangle {\rm AFC}\) を考えると、
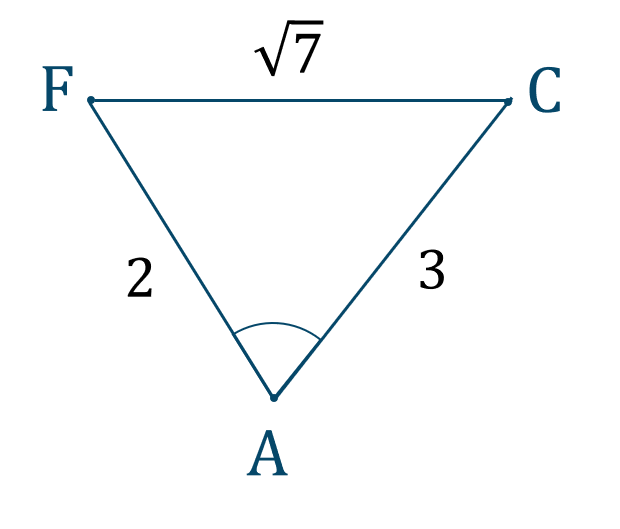
①〜③より、次のようになります。
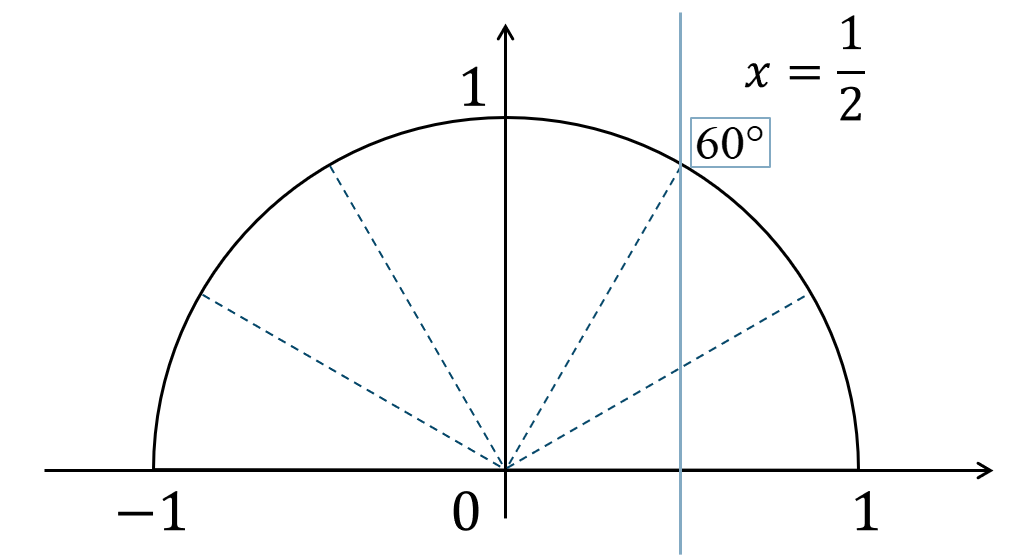
また、\(\angle{\rm AFC}=\theta\) として、
\(\cos{\theta}\) において余弦定理を用いると、$$\hspace{ 10 pt}(\sqrt{7})^2=2^2+3^2-2\cdot2\cdot3\cdot\cos{\theta}$$$$\hspace{ 30 pt}7=4+9-12\cos{\theta}$$$$\hspace{ 30 pt}7=13-12\cos{\theta}$$移項すると、$$\hspace{ 10 pt}12\cos{\theta}=13-7$$$$\hspace{ 10 pt}12\cos{\theta}=6$$両辺を \(12\) で割ると、$$\hspace{ 10 pt}\cos{\theta}=\frac{6}{12}$$$$\hspace{ 32 pt}=\frac{1}{2}$$単位円上に表すと、
よって、答えは$$~~~\theta=60^\circ$$となります。
問題解説(2)
\(\triangle {\rm AFC}\) は値を書き入れると、次のようになります。
\(\triangle {\rm AFC}\) の面積を \(S\) とすると、$$\hspace{ 10 pt}S=\frac{1}{2}\cdot2\cdot3\cdot\sin{60^\circ}$$$$\hspace{ 20 pt}=3\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 20 pt}=\frac{3\sqrt{3}}{2}$$よって、答えは$$~~~S=\frac{3\sqrt{3}}{2}$$となります。
問題解説(3)
三角錐 \({\rm BAFC}\) は \(\triangle {\rm ABC}\) を底面と考えると、高さが \({\rm BF}\) の三角錐となります。
\(\triangle {\rm ABC}\) の面積は、
図より、$$\hspace{ 10 pt}\frac{1}{2}\cdot\sqrt{6}\cdot1=\frac{\sqrt{6}}{2}$$また、高さ \({\rm BF}\) は、$$\hspace{ 10 pt}{\rm BF}={\rm AE}=\sqrt{3}$$
したがって、三角錐 \({\rm BAFC}\) の体積 \(V\) は、$$\hspace{ 10 pt}V=\frac{1}{3}\cdot \frac{\sqrt{6}}{2}\cdot\sqrt{3}$$$$\hspace{ 20 pt}=\frac{3\sqrt{2}}{6}$$$$\hspace{ 20 pt}=\frac{\sqrt{2}}{2}$$よって、答えは$$~~~V=\frac{\sqrt{2}}{2}$$となります。
問題解説(4)
\(\triangle {\rm AFC}\) を底面としたとき、三角錐 \({\rm BAFC}\) の体積 \(V\) は、
$$\hspace{ 10 pt}V=\frac{1}{3}\cdot\triangle {\rm AFC}\cdot{\rm BI}$$ここで、(2)の答えより$$~~~\triangle {\rm AFC}=\frac{3\sqrt{3}}{2}$$(3)の答えより、$$~~~V=\frac{\sqrt{2}}{2}$$これらを代入すると、$$\hspace{ 10 pt}\frac{\sqrt{2}}{2}=\frac{1}{3}\cdot\frac{3\sqrt{3}}{2}\cdot{\rm BI}$$両辺を入れ替えると、$$\hspace{ 10 pt}\frac{1}{3}\cdot\frac{3\sqrt{3}}{2}\cdot{\rm BI}=\frac{\sqrt{2}}{2}$$$$\hspace{ 31 pt}\frac{\sqrt{3}}{2}\cdot{\rm BI}=\frac{\sqrt{2}}{2}$$両辺を \({\Large \frac{2}{\sqrt{3}}}\) で割ると、$$\hspace{ 10 pt}{\rm BI}=\frac{\sqrt{6}}{3}$$よって、答えは$$~~~{\rm BI}=\frac{\sqrt{6}}{3}$$となります。
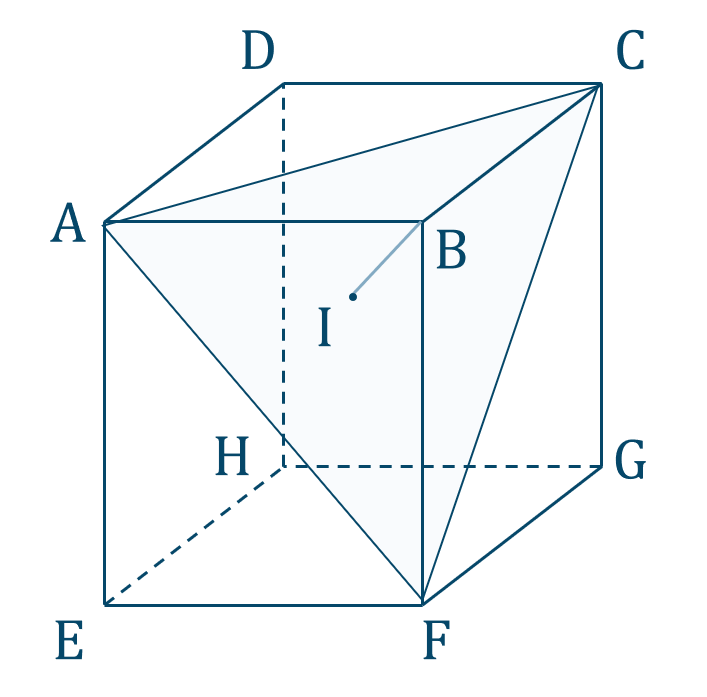
今回のまとめ
立体図形の計量は、まずは必要な部分を平面図形として抜き出して考えましょう。また、三角錐の体積は底面の位置で求め方が変わるのを利用しましょう。
