正四面体の計量

正四面体の計量
問題解説：正四面体の計量
今回のまとめ

正四面体の計量

Point：正四面体の計量立体図形の基本解法は、
「必要な部分を平面図形として抜き出して考える」
これが重要となります。

正四面体の計量では、４つの面がすべて正三角形となっている点を利用しましょう。

・三角形の高さと正弦
三角形の高さを求めるとき、

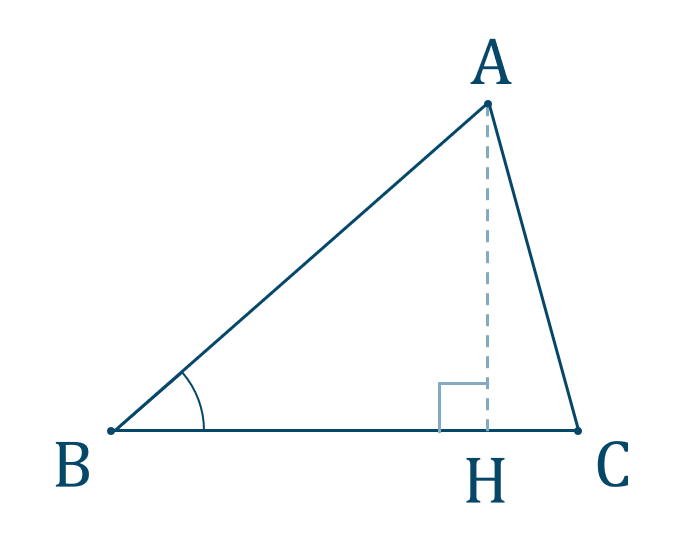
図のように $\angle{\rm B}$ の 正弦 $\sin{}$ の値がわかっていれば、

$$\sin{{\rm B}}=\frac{{\rm AH}}{{\rm AB}}$$

これより、${\rm AH}$ を求めることができます。

問題解説：正四面体の計量

問題解説(1)

問題１辺の長さが $3$ の正四面体 ${\rm ABCD}$ について、辺${\rm BC}$ の中点を ${\rm M}$、頂点 ${\rm A}$ から線分 ${\rm MD}$ に下ろした垂線を ${\rm AH}$ とするとき、次の値を求めよ。
${\small (1)}$ $\cos{\angle{\rm AMD}}$

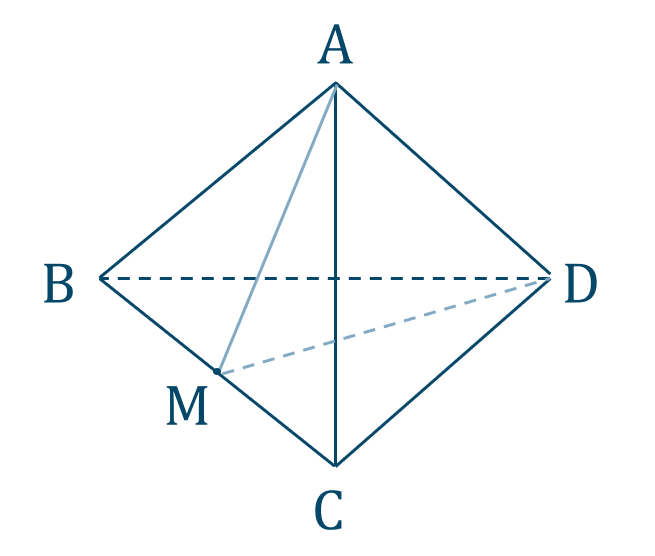
与えられた正四面体は次のようになります。

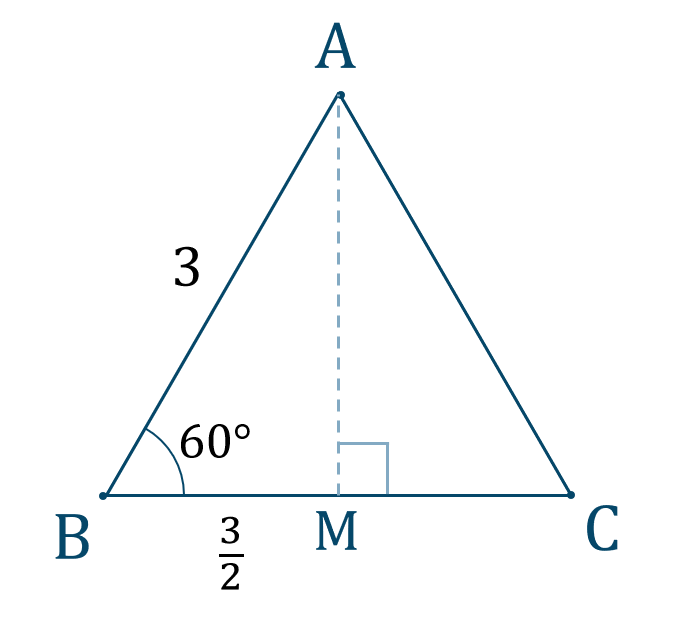
$\triangle {\rm ABC}$ について考えると、

これより、$\triangle {\rm ABM}$ は $1:2:\sqrt{3}$ の直角三角形となるので、$$\hspace{ 10 pt}{\rm AB}:{\rm AM}=2:\sqrt{3}$$$$\hspace{ 28 pt}2{\rm AM}=\sqrt{3}{\rm AB}$$$$\hspace{ 32 pt}{\rm AM}=\frac{\sqrt{3}}{2}{\rm AB}$$よって、${\rm AB}=3$ より、$$~~~{\rm AM}=\frac{3\sqrt{3}}{2}$$となります。

また、$\triangle {\rm DBC}$ でも同様に考えると、$$~~~{\rm DM}=\frac{3\sqrt{3}}{2}$$となります。

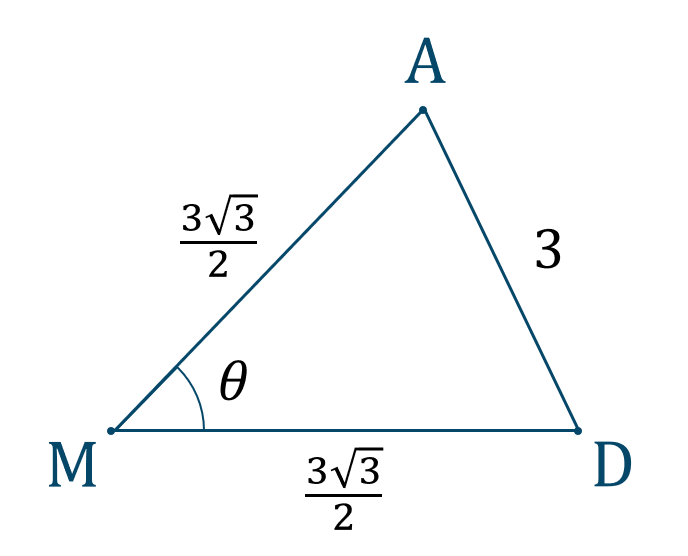
次に $\triangle {\rm AMD}$ について考えると、図形は次のようになります。

$\angle{\rm AMD}=\theta$ とすると、
$\triangle {\rm AMD}$ について、余弦定理を用いると、$$\hspace{ 10 pt}3^2=\left(\frac{3\sqrt{3}}{2}\right)^2+\left(\frac{3\sqrt{3}}{2}\right)^2$$$$\hspace{ 30 pt}-2\cdot\left(\frac{3\sqrt{3}}{2}\right)\cdot\left(\frac{3\sqrt{3}}{2}\right)\cdot\cos{\theta}$$$$\hspace{ 10 pt}9=\frac{27}{4}+\frac{27}{4}-\frac{27}{2}\cos{\theta}$$$$\hspace{ 10 pt}9=\frac{27+27}{4}-\frac{27}{2}\cos{\theta}$$$$\hspace{ 10 pt}9=\frac{54}{4}-\frac{27}{2}\cos{\theta}$$$$\hspace{ 10 pt}9=\frac{27}{2}-\frac{27}{2}\cos{\theta}$$両辺に $2$ をかけると、$$\hspace{ 10 pt}18=27-27\cos{\theta}$$移項すると、$$\hspace{ 10 pt}27\cos{\theta}=27-18$$$$\hspace{ 10 pt}27\cos{\theta}=9$$両辺を $27$ で割ると、$$\hspace{ 10 pt}\cos{\theta}=\frac{9}{27}$$$$\hspace{ 32 pt}=\frac{1}{3}$$よって、答えは$$~~~\cos{\angle{\rm AMD}}=\frac{1}{3}$$となります。

問題解説(2)

問題１辺の長さが $3$ の正四面体 ${\rm ABCD}$ について、辺${\rm BC}$ の中点を ${\rm M}$、頂点 ${\rm A}$ から線分 ${\rm MD}$ に下ろした垂線を ${\rm AH}$ とするとき、次の値を求めよ。
${\small (2)}$ 辺 ${\rm AH}$

相互関係の公式より、$$\hspace{ 10 pt}\sin^2{\theta}+\cos^2{\theta}=1$$移項すると、$$\hspace{ 10 pt}\sin^2{\theta}=1-\cos^2{\theta}$$$\cos{\theta}$ の値を代入すると、$$\hspace{ 10 pt}\sin^2{\theta}=1-\left(\frac{1}{3}\right)^2$$$$\hspace{ 35 pt}=1-\frac{1}{9}$$$$\hspace{ 35 pt}=\frac{9-1}{9}$$$$\hspace{ 35 pt}=\frac{8}{9}$$$\sin{\theta}>0$ であることより、$$\hspace{ 10 pt}\sin{\theta}=\sqrt{\frac{8}{9}}$$$$\hspace{ 31 pt}=\frac{\sqrt{8}}{\sqrt{9}}$$$$\hspace{ 31 pt}=\frac{2\sqrt{2}}{3}$$
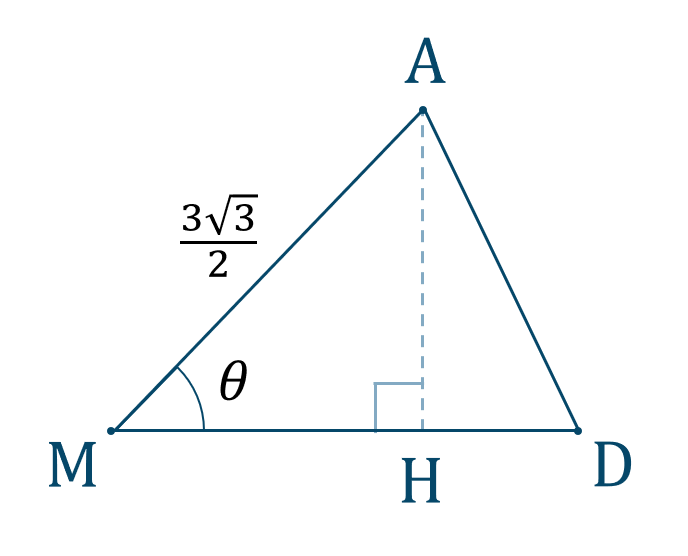
また、$\triangle {\rm AMD}$ と垂線との交点 ${\rm H}$ は次の図のようになります。

ここで、直角三角形の三角比の定義より、$$\hspace{ 10 pt}\sin{\theta}=\frac{{\rm AH}}{{\rm AM}}$$両辺を入れ替えて、${\rm AM}$ をかけると、$$\hspace{ 10 pt}\frac{{\rm AH}}{{\rm AM}}=\sin{\theta}$$$$\hspace{ 13 pt}{\rm AH}={\rm AM}\cdot\sin{\theta}$$値を代入すると、$$\hspace{ 10 pt}{\rm AH}=\frac{3\sqrt{3}}{2}\cdot\frac{2\sqrt{2}}{3}$$$$\hspace{ 27 pt}=\sqrt{6}$$よって、答えは$$~~~{\rm AH}=\sqrt{6}$$となります。

問題解説(3)

問題１辺の長さが $3$ の正四面体 ${\rm ABCD}$ について、辺${\rm BC}$ の中点を ${\rm M}$、頂点 ${\rm A}$ から線分 ${\rm MD}$ に下ろした垂線を ${\rm AH}$ とするとき、次の値を求めよ。
${\small (3)}$ 正四面体 ${\rm ABCD}$ の体積

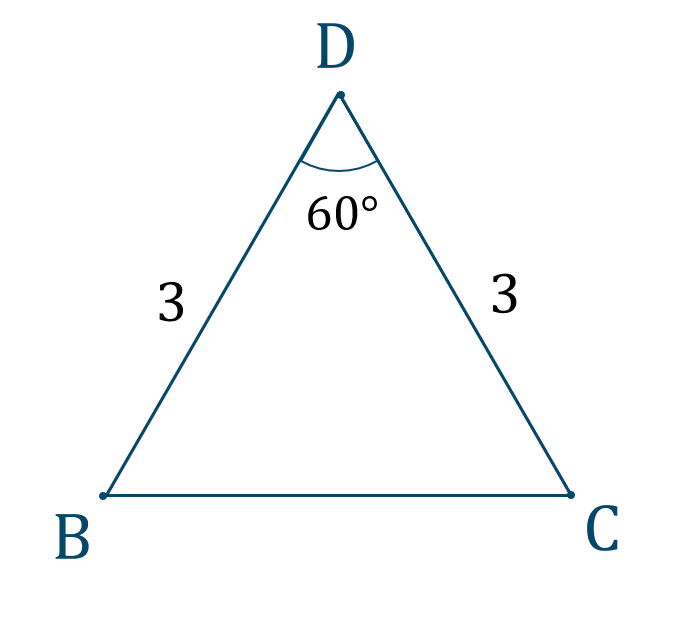
$\triangle {\rm DBC}$ について考えると、

図より、$\triangle {\rm DBC}$ の面積 $S$ は、$$\hspace{ 10 pt}S=\frac{1}{2}\cdot3\cdot3\cdot\sin{60^\circ}$$$$\hspace{ 20 pt}=\frac{9}{2}\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 20 pt}=\frac{9\sqrt{3}}{4}$$
よって、$\triangle {\rm DBC}$ を底面、高さを ${\rm AH}=\sqrt{6}$ として、正四面体 ${\rm ABCD}$ の体積 $V$ を求めると、$$\hspace{ 10 pt}V=\frac{1}{3}\cdot\triangle {\rm DBC}\cdot{\rm AH}$$$$\hspace{ 20 pt}=\frac{1}{3}\cdot\frac{9\sqrt{3}}{4}\cdot\sqrt{6}$$$$\hspace{ 20 pt}=\frac{9\cdot3\sqrt{2}}{12}$$$$\hspace{ 20 pt}=\frac{9\sqrt{2}}{4}$$よって、答えは$$~~~\frac{9\sqrt{2}}{4}$$となります。