座標を利用した等式の証明

2018.05.042020.06.09

座標を利用した等式の証明の方法
問題解説：座標を利用した等式の証明
今回のまとめ

座標を利用した等式の証明の方法

Point：座標を利用した等式の証明三角形 $ABC$ と辺 $BC$ の中点 $M$ の４つの座標をすべて文字でおくと未知数が多くなってしまいます。
次のように座標軸と原点を利用することで未知数の数を少なくすることができます。

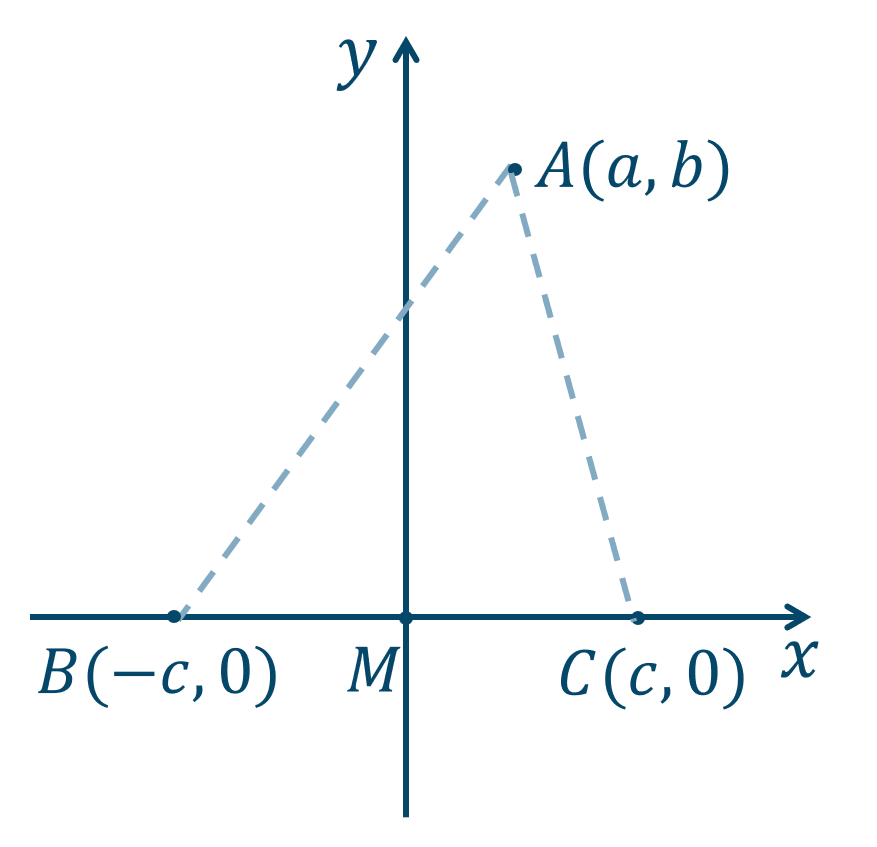
$BC$ の中点 $M$ を原点におくことで、点 $B$ と点 $C$ が原点で対称となり未知数を１つで表すことでできます。

問題解説：座標を利用した等式の証明

問題三角形 $ABC$ と辺 $BC$ の中点 $M$ において、次の等式が成り立つことを証明せよ。$$~~~AB^2+AC^2=2(AM^2+BM^2)$$

[証明]
線分 $BC$ の中点 $M$ を原点におき、３点 $A,B,C$ を次のように座標平面上に表します。
$$~~~A(a,b)~,~B(-c,0)~,~C(c,0)~,~M(0,0)$$
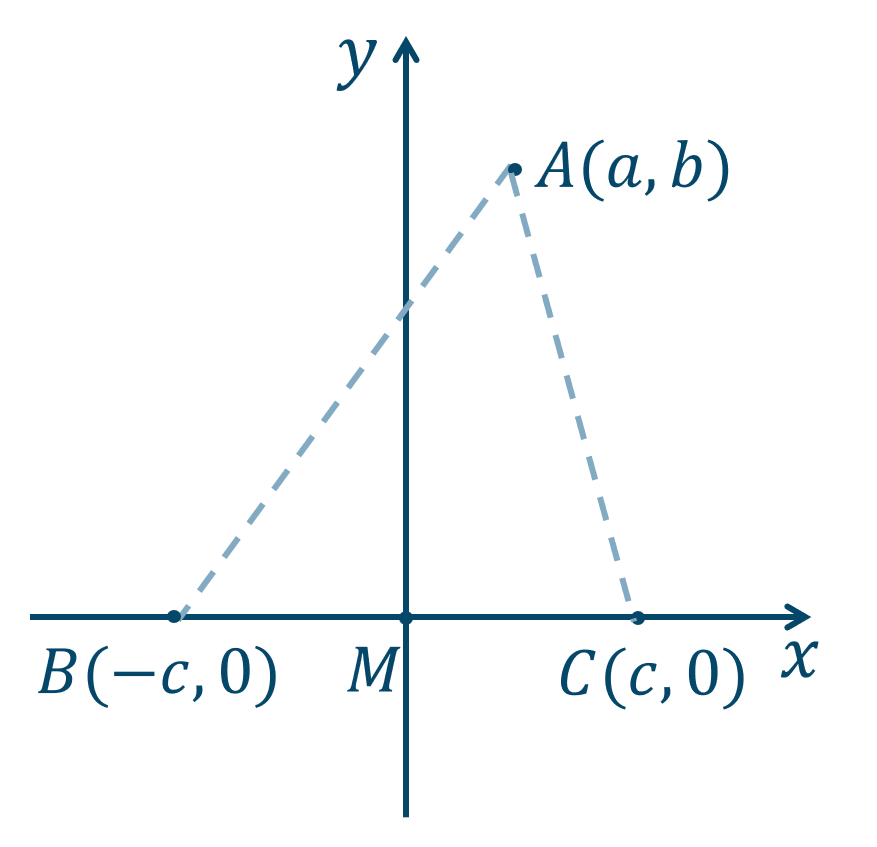
$AB$ と $AC$ の２点間の距離の公式より、$$~~~~~~AB^2$$$$~=(-c-a)^2+(0-b)^2$$$$~=c^2+2ac+a^2+b^2$$$$~=a^2+b^2+c^2+2ac$$また、$$~~~~~~AC^2$$$$~=(c-a)^2+(0-b)^2$$$$~=c^2-2ac+a^2+b^2$$$$~=a^2+b^2+c^2-2ac$$よって、$$~~~~~~AB^2+AC^2$$$$~=(a^2+b^2+c^2+2ac)$$$$\hspace{40pt}+(a^2+b^2+c^2-2ac)$$$$~=2a^2+2b^2+2c^2$$$$~=2(a^2+b^2+c^2)~\cdots{\large ①}$$
次に、$AM$ と $BM$ の２点間の距離の公式より、$$~~~~~~AM^2$$$$~=(0-a)^2+(0-b)^2$$$$~=a^2+b^2$$また、$$~~~~~~BM^2$$$$~=\{0-(-c)\}^2$$$$~=c^2$$よって、$$~~~~~~2(AM^2+BM^2)$$$$~=2(a^2+b^2+c^2)~\cdots{\large ②}$$
したがって、①と②より、$$~~~AB^2+AC^2=2(AM^2+BM^2)$$[終]