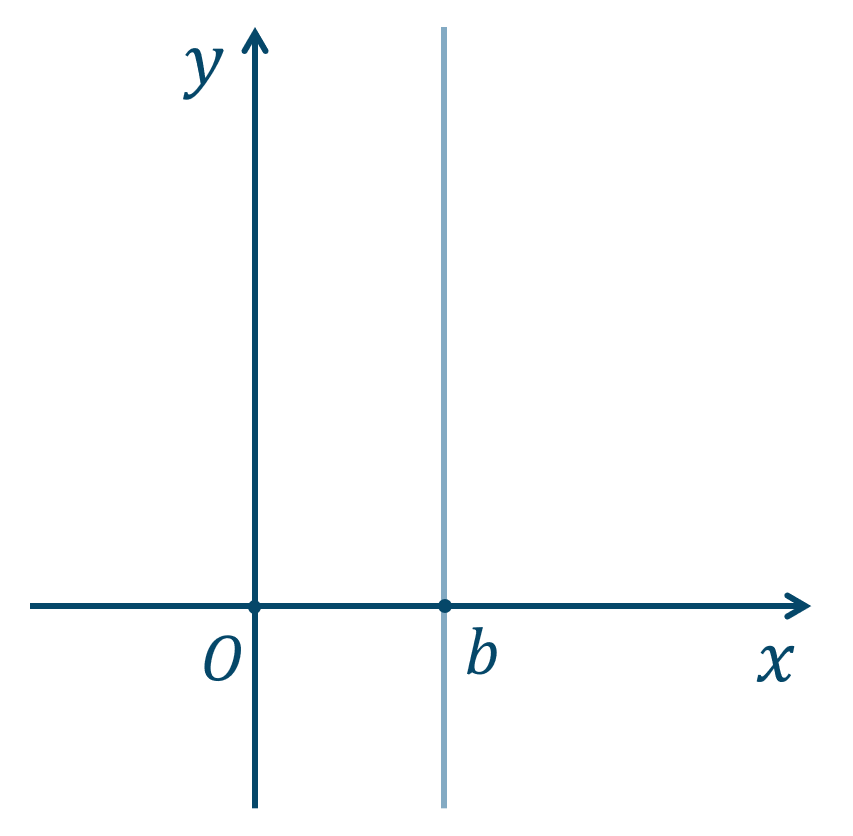直線の方程式の解法
\(x\) 軸に平行な直線の方程式は、
\(y\) 座標が常に \(a\) となるので、
\(y\) 軸に平行な直線の方程式は、
\(x\) 座標が常に \(b\) となるので、
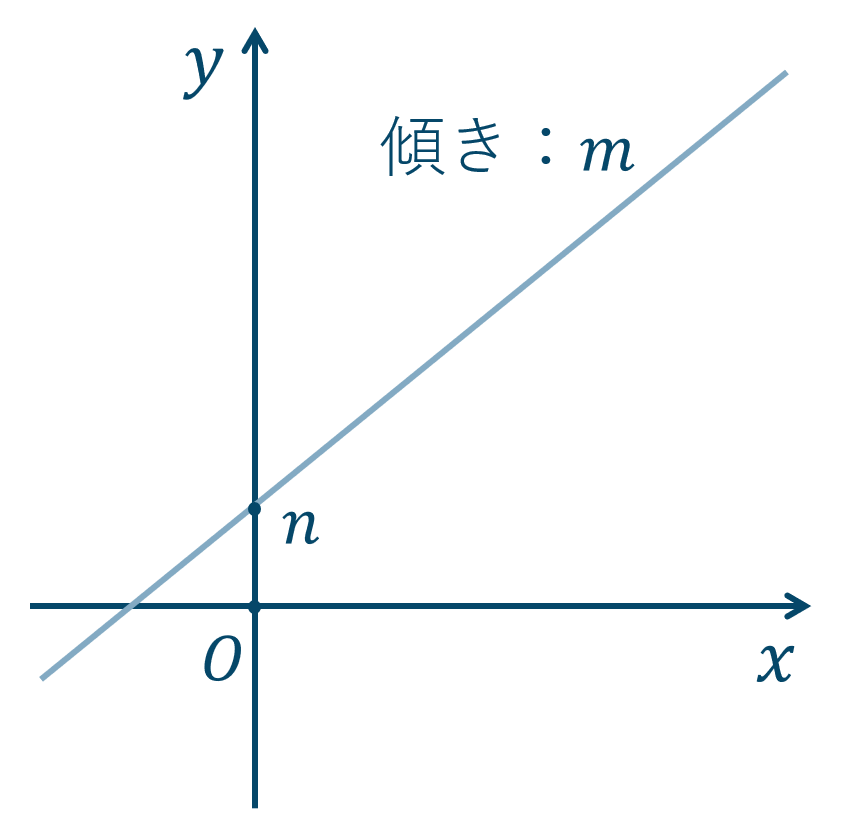
・傾きと \(y\) 切片
傾きが \(m\) で、\(y\) 切片が \(n\) の直線の方程式は、
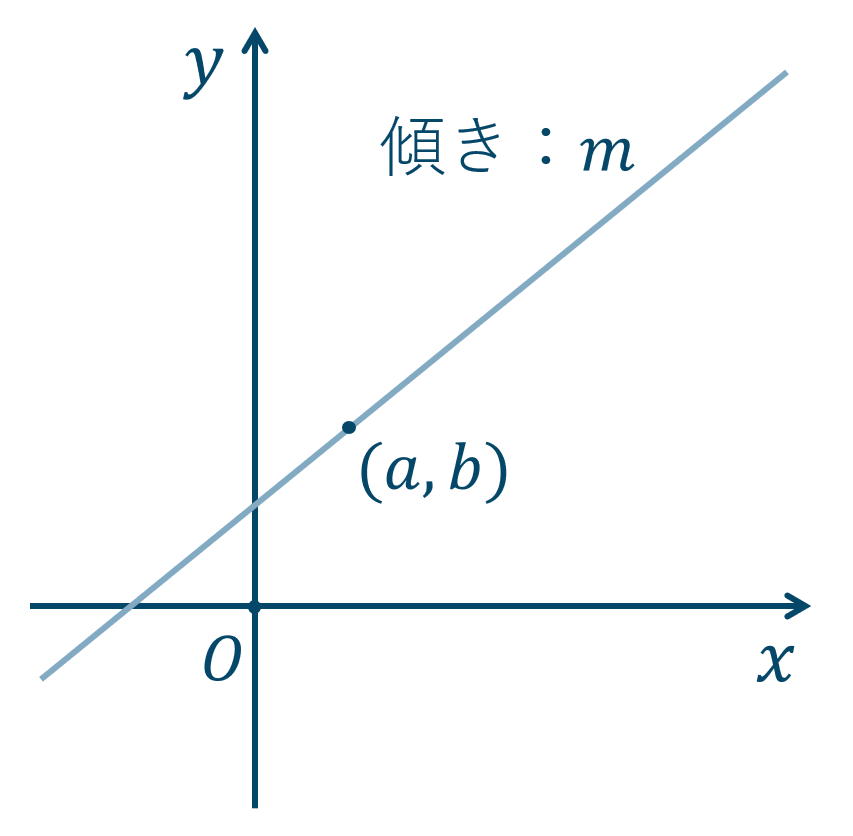
・傾きと1点
傾きが \(m\) で、点 \((a,b)\) を通る直線の方程式は、
・直線の方程式の一般形
次の式を直線の方程式の一般形といいます。
\(a\neq 0\) または \(b\neq 0\) のとき、
問題解説:直線の方程式
問題解説(1)
\({\small (1)}~\)点 \((2,3)\) を通り、\(x\) 軸に平行な直線
点 \((2,3)\) を通り、\(x\) 軸に平行な直線の方程式は、\(y\) 座標が常に \(3\) になるので、$$~~~y=3$$
また、一般形は移項すると、$$~~~y-3=0$$となります。
問題解説(2)
\({\small (2)}~\)点 \((2,3)\) を通り、\(y\) 軸に平行な直線
点 \((2,3)\) を通り、\(y\) 軸に平行な直線の方程式は、\(x\) 座標が常に \(2\) になるので、$$~~~x=2$$
また、一般形は移項すると、$$~~~x-2=0$$となります。
問題解説(3)
\({\small (3)}~\)傾きが \(3\) で \(y\) 切片が \(-2\) の直線
傾きが \(3\) で、\(y\) 切片が \(-2\) の直線の方程式は、$$~~~y=3x-2$$
また、一般形は移項すると、$$\hspace{ 10 pt}-3x+y+2=0$$両辺に \(-1\) をかけると、$$\hspace{ 18 pt}3x-y-2=0$$となります。
問題解説(4)
\({\small (4)}~\)傾きが \(3\) で、点 \((2,3)\) を通る直線
傾きが \(3\) で、点 \((2,3)\) を通る直線の方程式は、$$~~~~y-3=3(x-2)$$$$\hspace{ 10 pt}y-3=3x-6$$移項すると、$$\hspace{ 10 pt}y=3x-6+3$$$$\hspace{ 10 pt}y=3x-3$$
また、一般形は移項すると、$$\hspace{ 10 pt}-3x+y+3=0$$両辺に \(-1\) をかけると、$$\hspace{ 18 pt}3x-y-3=0$$となります。
今回のまとめ
直線の方程式を求めるときは、それぞれの条件に合った条件式を用いて計算しましょう。