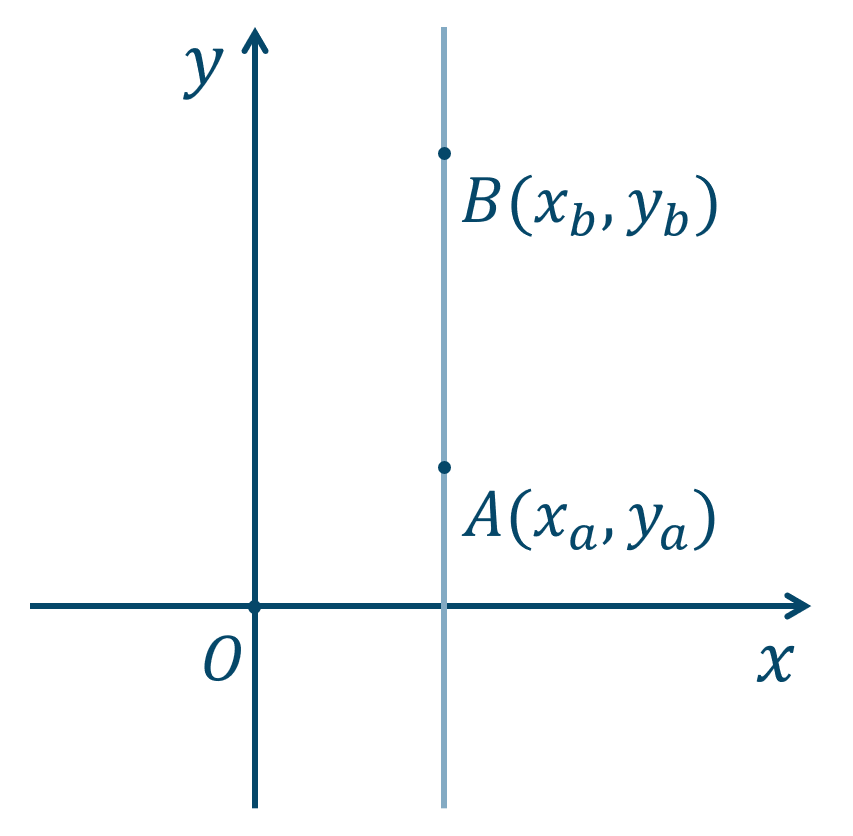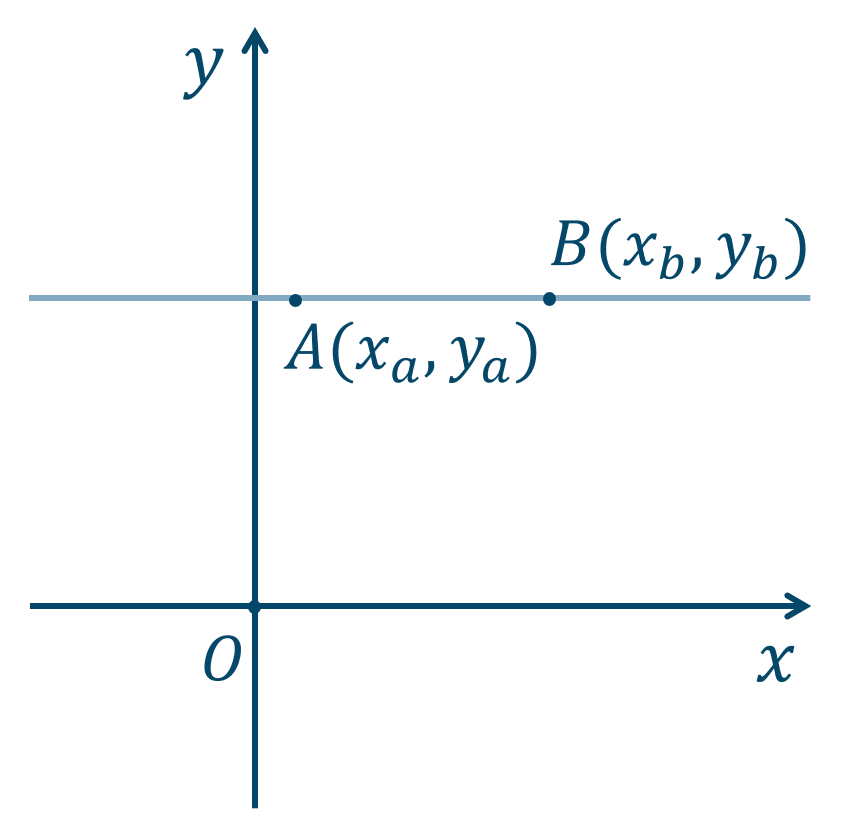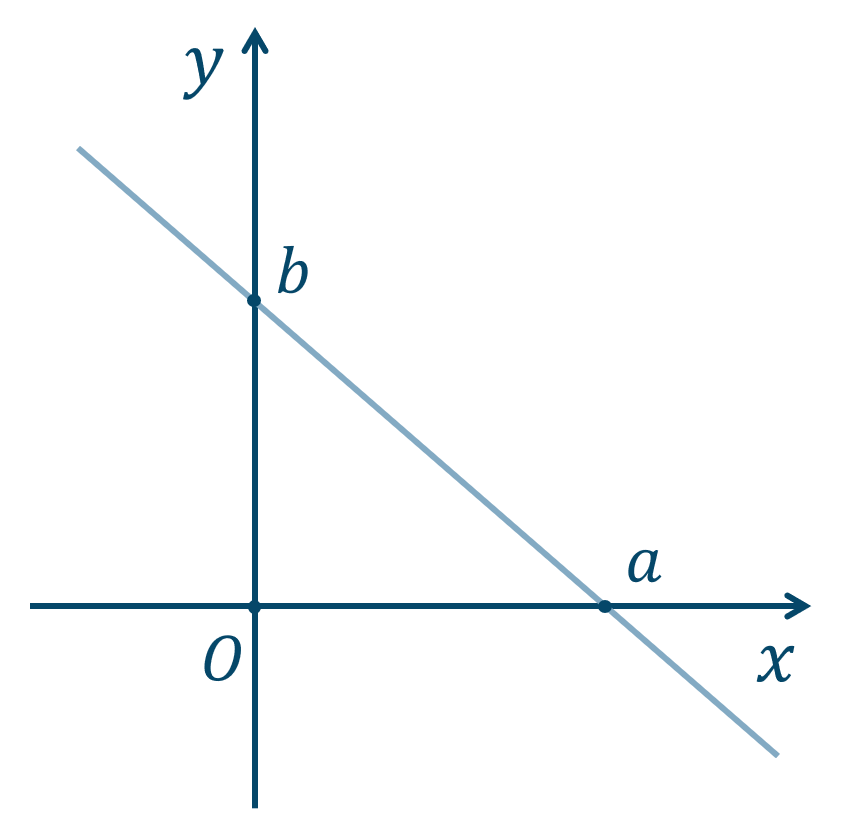２点を通る直線の方程式

2018.05.052020.06.09

２点を通る直線の方程式の解法
問題解説：２点を通る直線の方程式
今回のまとめ

２点を通る直線の方程式の解法

Point：２点を通る直線の方程式・２点を通る直線
２点 $(x_a,y_a)~,~(x_b,y_b)$ を通る直線の方程式は、
① $x_a\neq x_b$ かつ $y_a\neq y_b$ のとき

$$y-y_a=\frac{y_b-y_a}{x_b-x_a} (x-x_a)$$

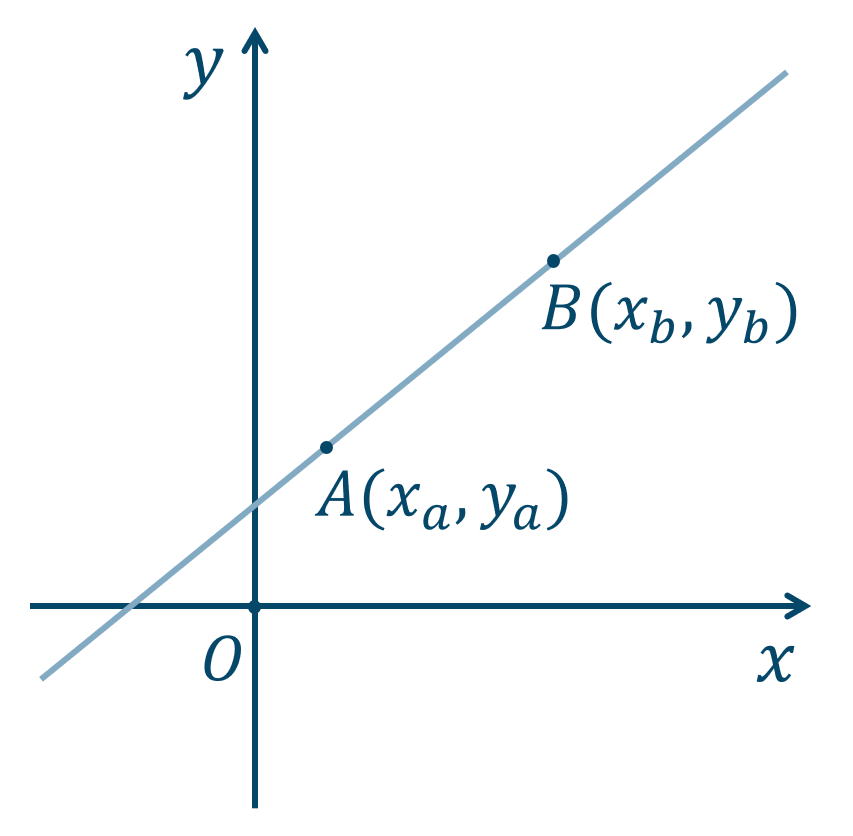
傾きの部分が、
分子が $y$ の増加量 $y_b-y_a$
分母が $x$ の増加量 $x_b-x_a$
となっています。引く順番を分母分子で揃えることに注意しましょう。

② $x_a=x_b$ のとき

$x$ 座標が同じであり、$y$ 軸に平行な直線となるので、

$$x=x_a$$

となります。

③ $y_a=y_b$ のとき

$y$ 座標が同じであり、$x$ 軸に平行な直線となるので、

$$y=y_a$$

となります。

・切片を通る直線
２点 $(a,0)~,~(0,b)$ のように、$x$ 切片と $y$ 切片が与えられた直線の方程式は、

$$\frac{x}{a}+\frac{y}{b}=1$$

となります。

問題解説：２点を通る直線の方程式

問題解説(1)

問題次の直線の方程式を求めよ。
${\small (1)}~$２点 $(2,3)~,~(-2,1)$ を通る直線

２点 $(2,3)~,~(-2,1)$ を通るので、$$\hspace{ 10 pt}y-3=\frac{1-3}{-2-2}(x-2)$$$$\hspace{ 10 pt}y-3=\frac{-2}{-4}(x-2)$$$$\hspace{ 10 pt}y-3=\frac{1}{2}(x-2)$$移項すると、$$\hspace{ 10 pt}y=\frac{1}{2}x-1+3$$$$\hspace{ 10 pt}y=\frac{1}{2}x+2$$よって、答えは $y={\Large \frac{1}{2}} x+2$ となります。

問題解説(2)

問題次の直線の方程式を求めよ。
${\small (2)}~$２点 $(2,3)~,~(2,-5)$ を通る直線

２点 $(2,3)~,~(2,-5)$ は $x$ 座標が等しいので $y$ 軸に平行な直線となります。よって、答えは $x=2$ となります。

問題解説(3)

問題次の直線の方程式を求めよ。
${\small (3)}~$２点 $(3,1)~,~(-2,1)$ を通る直線

２点 $(3,1)~,~(-2,1)$ は $y$ 座標が等しいので $x$ 軸に平行な直線となります。よって、答えは $y=1$ となります。

問題解説(4)

問題次の直線の方程式を求めよ。
${\small (4)}~$２点 $(2,0)~,~(0,1)$ を通る直線

２点 $(2,0)~,~(0,1)$ を通ることより、$x$ 切片と $y$ 切片がわかるので、直線の方程式は次のようなります。$$~~~\frac{x}{2}+\frac{y}{1}=1$$$$\hspace{ 12 pt}\frac{x}{2}+y=1$$移項すると、$$\hspace{ 10 pt}y=-\frac{1}{2}x+1$$よって、答えは $y=-{\Large \frac{1}{2}}x+1$ となります。