平行な直線と垂直な直線の解法
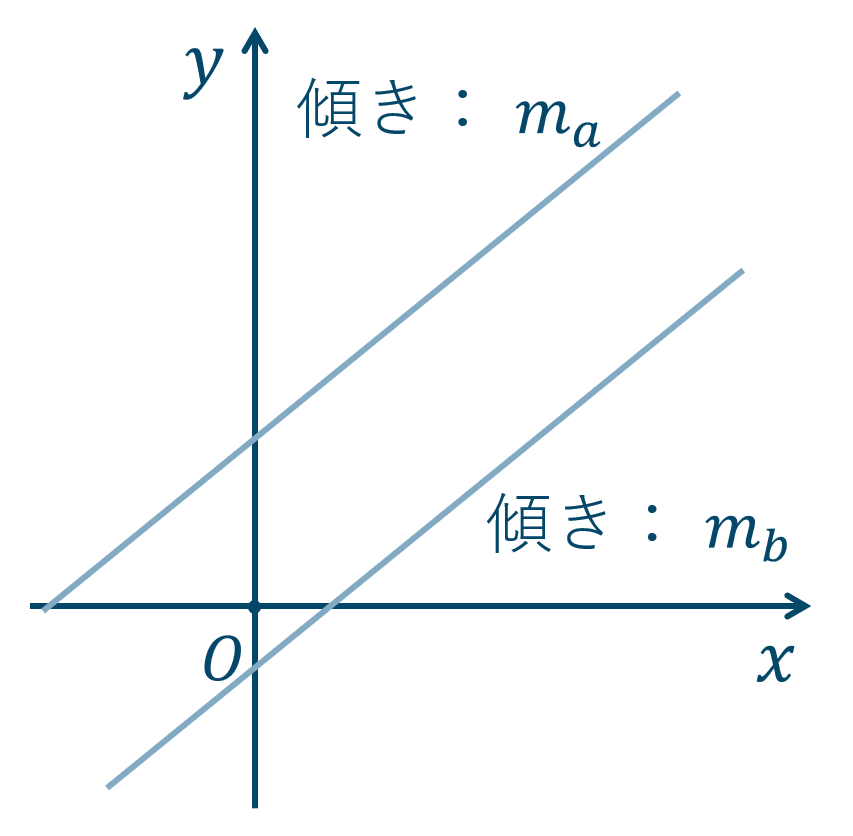
次の2直線について、$$~~~\biggl\{ \begin{eqnarray} ~y=m_ax+n_a \\ ~y=m_bx+n_b\end{eqnarray}$$この2直線が平行のとき、
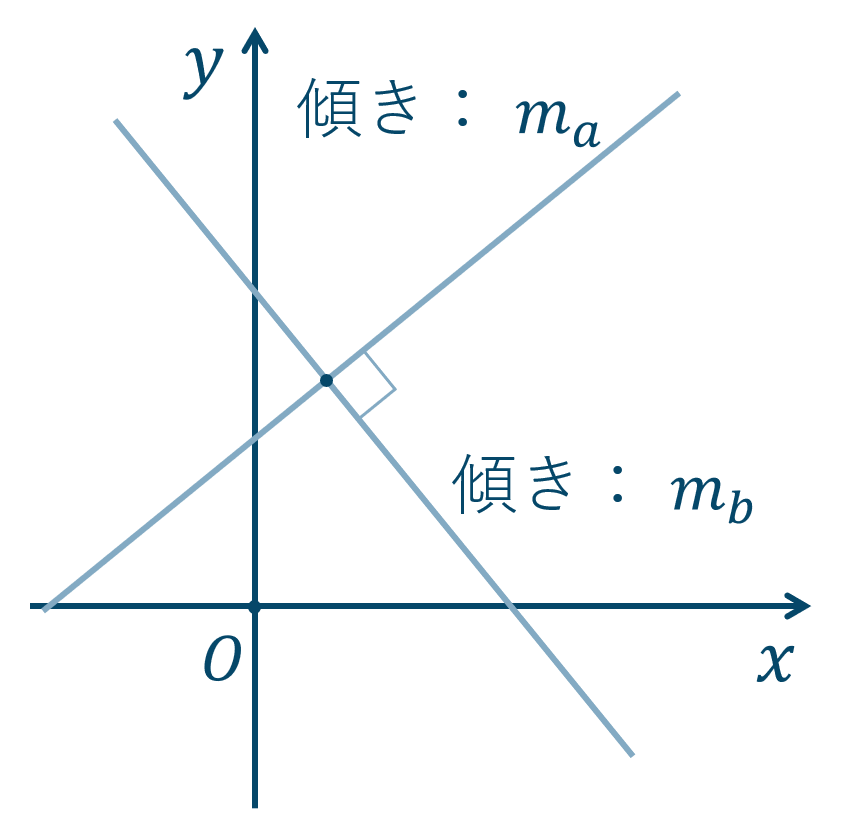
この2直線が垂直のとき、
これらを用いて傾きを求めましょう。
・一般形の平行と垂直
点 \((x_p,y_p)\) を通り、直線 \(ax+by+c=0\) について、
平行な直線は、
垂直な直線は、
傾きを求める方法でも解けますが、この公式を覚えておくと計算が楽になります。
問題解説:平行な直線と垂直な直線
問題解説(1)
\({\small (1)}~\)点 \((-2,1)\) を通り、直線 \(y=-3x+9\) に平行な直線と垂直な直線
直線 \(y=-3x+9\) の傾きが \(-3\) となります。
この直線に平行な直線の傾きは \(-3\) となり、点 \((-2,1)\) を通るので、$$\hspace{ 10 pt}y-1=-3\{x-(-2)\}$$$$\hspace{ 10 pt}y-1=-3(x+2)$$移項して計算すると、$$\hspace{ 10 pt}y=-3x-6+1$$$$\hspace{ 10 pt}y=-3x-5$$
この直線に垂直な直線の傾きを \(m\) とすると、$$~~~-3\times m=-1$$$$\hspace{ 38 pt}m=\frac{1}{3}$$よって、傾きが \({\Large \frac{1}{3}}\) で、点 \((-2,1)\) を通るので、$$\hspace{ 10 pt}y-1=\frac{1}{3}\{x-(-2)\}$$$$\hspace{ 10 pt}y-1=\frac{1}{3}(x+2)$$移項して計算すると、$$\hspace{ 10 pt}y=\frac{1}{3}x+\frac{2}{3}+1$$$$\hspace{ 10 pt}y=\frac{1}{3}x+\frac{5}{3}$$
したがって、答えは平行な直線の方程式は、$$~~~y=-3x-5$$垂直な直線の方程式は、$$~~~y=\frac{1}{3}x+\frac{5}{3}$$となります。
問題解説(2)
\({\small (2)}~\)点\((2,3)\) を通り、直線 \(x-5y+1=0\) に平行な直線と垂直な直線
点 \((2,3)\) を通り、直線 \(x-5y+1=0\) について、
平行な直線の方程式は、$$\hspace{ 10 pt}1\cdot(x-2)+(-5)\cdot(y-3)=0$$$$\hspace{ 56 pt}x-2-5y+15=0$$$$\hspace{ 74 pt}x-5y+13=0$$
垂直な直線の方程式は、$$\hspace{ 10 pt}-5\cdot(x-2)-1\cdot(y-3)=0$$$$\hspace{ 42 pt}-5x+10-y+3=0$$$$\hspace{ 59 pt}-5x-y+13=0$$両辺に \(-1\) をかけると、$$\hspace{ 10 pt}5x+y-13=0$$
したがって、答えは、
平行な直線の方程式は、$$~~~x-5y+13=0$$垂直な直線の方程式は、$$~~~5x+y-13=0$$となります。
今回のまとめ
平行な直線と垂直な直線は傾きの関係式を覚えておきましょう。また、一般形の平行と垂直の公式は便利ですので使えるようになりましょう。