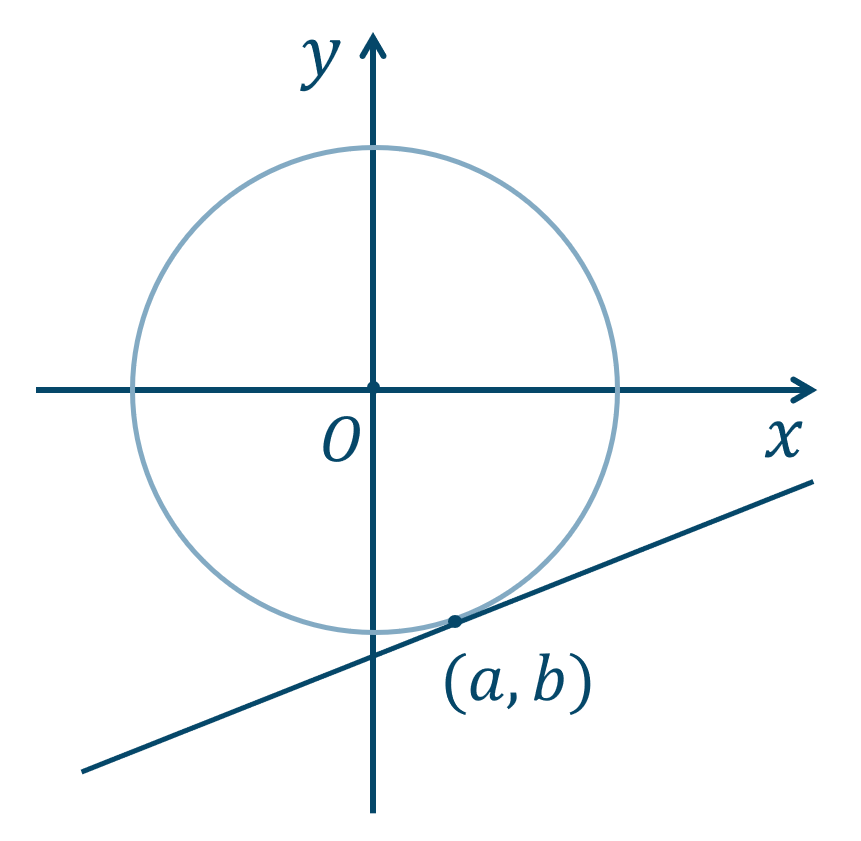
円の接線の方程式の解法
円 \(x^2+y^2=r^2\) 上の点 \((a,b)\) における接線の方程式は、
となります。
この公式は、円の方程式を$$~~~xx+yy=r^2$$と考えて、\(x,y\) のそれぞれ片方だけに \(a,b\) を代入すると覚えましょう。
・外部の点から引いた接線
円 \(x^2+y^2=r^2\) に外部の点 \((p,q)\) から引いた接線の方程式は、
① 接点の座標を \((a,b)\) とします。
② 円上にこの接点があることより、$$~~~a^2+b^2=r^2~\cdots {\small (a)}$$③ 接線の方程式を求めます。$$~~~ax+by=r^2~\cdots {\small (b)}$$④ この接線が点 \((p,q)\) を通ることより代入すると、$$~~~ap+bq=r^2~\cdots {\small (c)}$$⑤ \({\small (a)}\) と \({\small (c)}\) を連立して \(a,b\) の値を求めて、\({\small (b)}\) を代入して接線の方程式を求めます。
問題解説:円の接線の方程式
問題解説(1)
\({\small (1)}~\)円 \(x^2+y^2=5\) 上の点 \((-1,2)\) における接線の方程式を求めよ。
接線の方程式は、$$~~~(-1)\cdot x+2\cdot y=5$$$$\hspace{ 36 pt}-x+2y=5$$移項して、両辺に \(-1\) をかけると、$$\hspace{ 10 pt}-x+2y-5=0$$$$\hspace{ 18 pt}x-2y+5=0$$よって、答えは \(x-2y+5=0\) となります。
問題解説(2)
\({\small (2)}~\)円 \(x^2+y^2=10\) に点 \((5,5)\) から引いた接線の方程式を求めよ。
接点の座標を \((a,b)\) とすると、円上にこの接点があることより、$$~~~a^2+b^2=10~\cdots{\large ①}$$
また、接線の方程式は、$$~~~ax+by=10~\cdots{\large ②}$$この接線の方程式が点 \((5,5)\) を通るので、代入すると、$$~~~a\cdot 5+b\cdot 5=10$$$$\hspace{ 23 pt}5a+5b=10$$両辺を \(5\) で割ると、$$\hspace{ 10 pt}a+b=2$$移項すると、$$\hspace{ 10 pt}b=-a+2~\cdots{\large ③}$$
③を①に代入すると、$$\hspace{17pt} a^2+(-a+2)^2=10$$$$\hspace{ 10 pt}a^2+a^2-4a+4=10$$移項して計算すると、$$\hspace{ 10 pt}2a^2-4a+4-10=0$$$$\hspace{ 32 pt}2a^2-4a-6=0$$両辺を \(2\) で割ると、$$\hspace{ 10 pt} a^2-2a-3=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(a+1)(a-3)=0$$$$\hspace{ 67 pt}a=-1~,~3$$
( ⅰ ) \(a=-1\) のとき、③に代入すると、$$~~~b=-(-1)+2$$$$\hspace{ 15 pt}=1+2$$$$\hspace{ 15 pt}=3$$よって、\((a,b)=(-1,3)\) となるので②に代入すると、$$~~~(-1)\cdot x+3\cdot y=10$$$$\hspace{ 36 pt}-x+3y=10$$移項して、両辺に \(-1\) をかけると、$$\hspace{ 10 pt}-x+3y-10=0$$$$\hspace{ 18 pt}x-3y+10=0$$
( ⅱ ) \(a=3\) のとき、③に代入すると、$$~~~b=-3+2$$$$\hspace{ 15 pt}=-1$$よって、\((a,b)=(3,-1)\) となるので②に代入すると、$$~~~3\cdot x+(-1)\cdot y=10$$$$\hspace{ 43 pt}3x-y=10$$左辺に \(10\) を移項すると、$$\hspace{ 10 pt}3x-y-10=0$$
よって、( ⅰ )と( ⅱ )より答えは、$$~~~x-3y+10=0~,~3x-y-10=0$$となります。
今回のまとめ
接線の方程式はまずは公式を覚えましょう。また、外部の点から引いた接線は解法の手順を押さえておきましょう。