連立不等式の表す領域①

2018.05.162020.06.09

連立不等式の表す領域の解法
問題解説：連立不等式の表す領域①
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

連立不等式の表す領域の解法

Point：連立不等式の表す領域例えば、$$~~~\biggl\{ \begin{eqnarray}~y<x-2~\cdots{\large ①} \\ ~x>2~\cdots{\large ②} \end{eqnarray}$$
①は直線 $y=x-2$ の下側部分となるので、

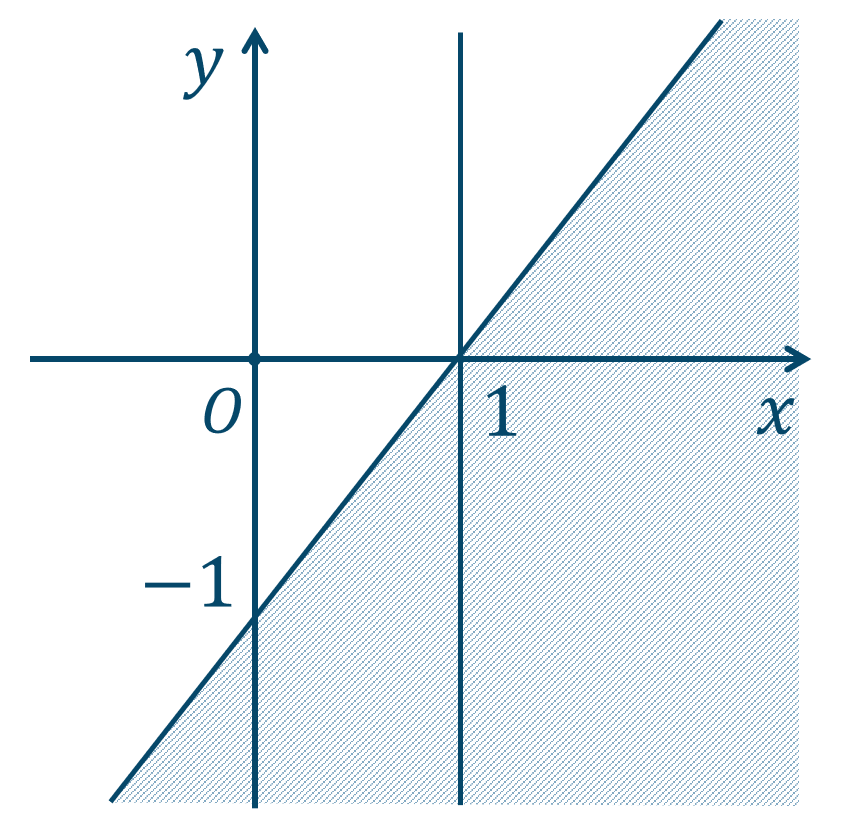
②は直線 $x=2$ の右側部分となるので、

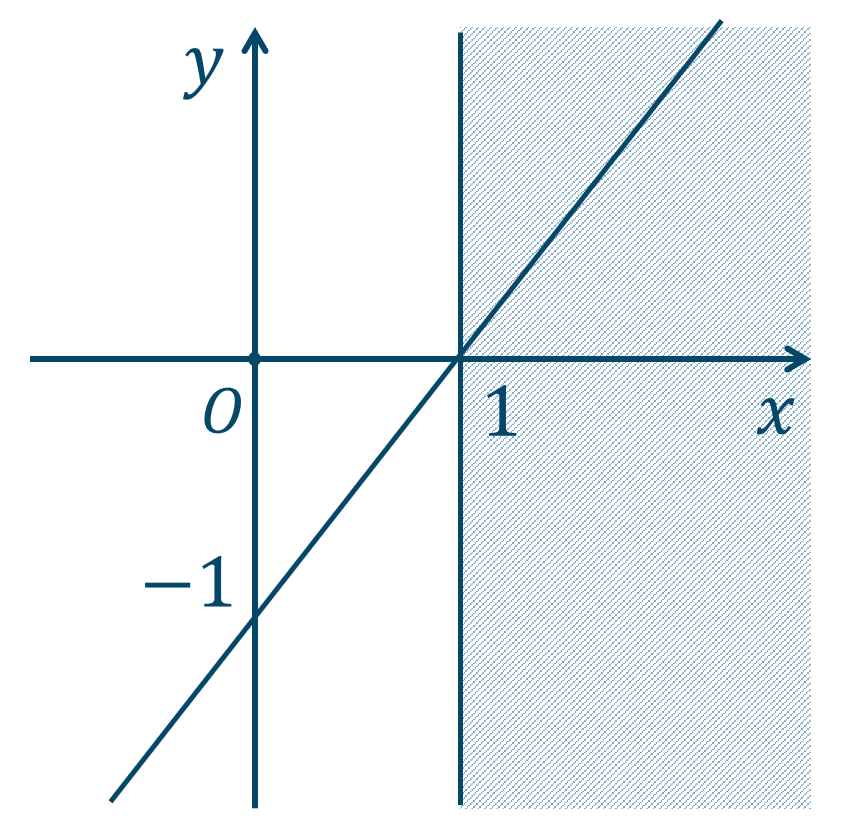
この２つの共通部分となるので、

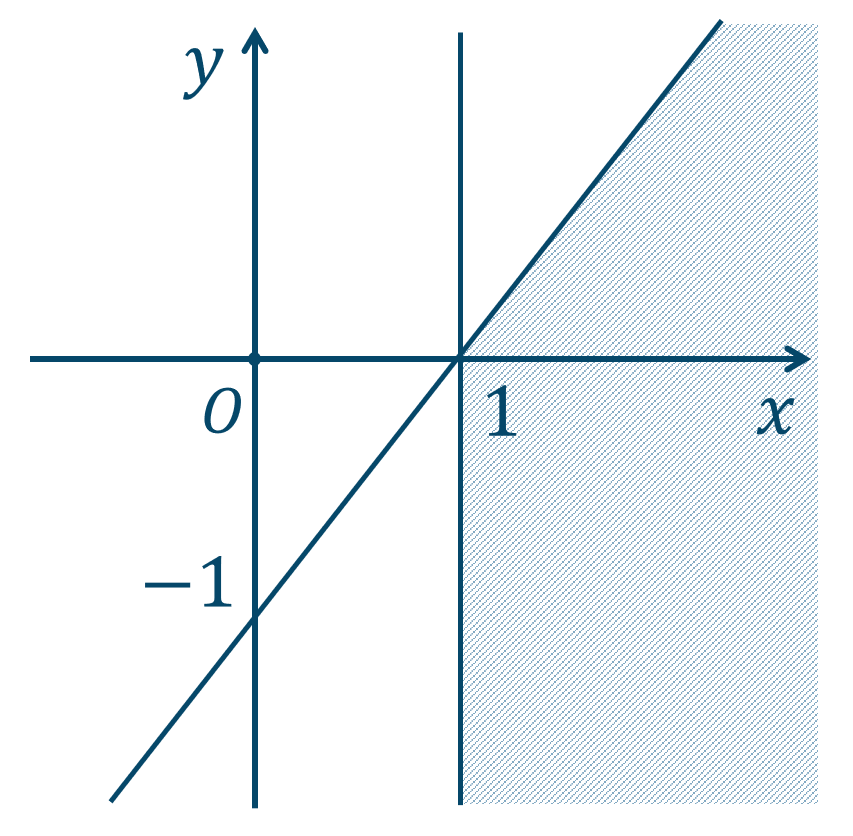
この連立不等式の領域は上の斜線部分となり、境界線は含みません。

このようにそれぞれの不等式の領域を表し、共通部分を求めましょう。

問題解説：連立不等式の表す領域①

問題解説(1)

問題次の不等式の表す領域を求めよ。$${\small (1)}~\biggl\{ \begin{eqnarray} ~x-y+1≧0 \\ ~3x+y+3≧0 \end{eqnarray}$$

$$~~~\biggl\{ \begin{eqnarray} ~x-y+1≧0 ~\cdots{\large ①} \\ ~3x+y+3≧0 ~\cdots{\large ②}\end{eqnarray}$$
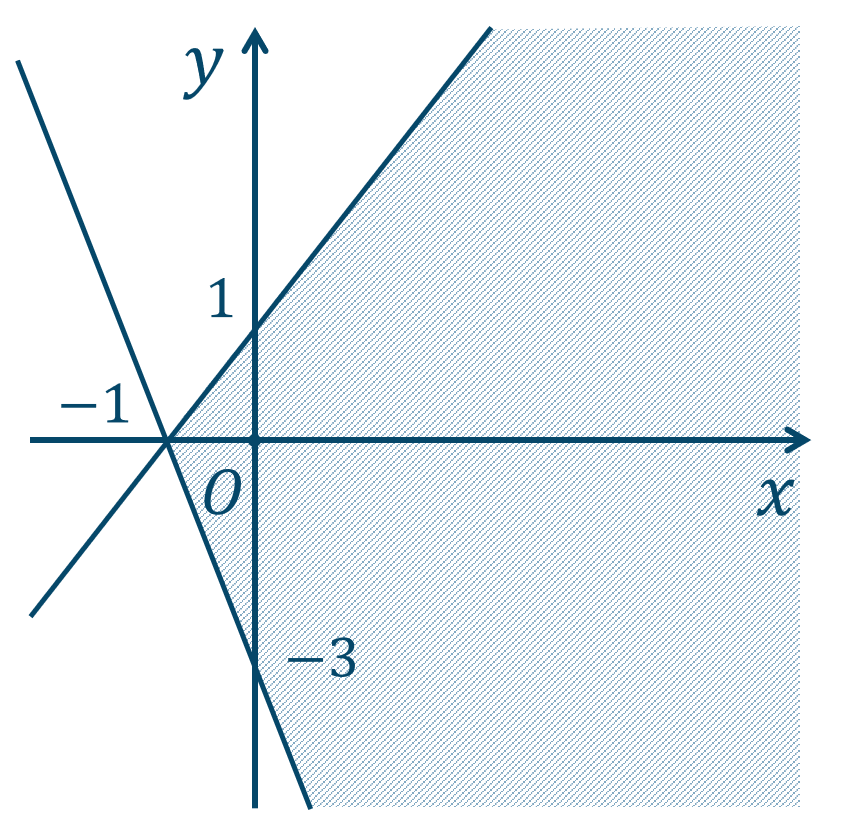
①について、式変形すると、$$~~~x-y+1≧0$$$$\hspace{ 37 pt}-y≧-x-1$$両辺に $-1$ をかけると、不等号の向きが逆になるので、$$\hspace{ 10 pt}y≦x+1$$よって、①は直線 $y=x+1$ の下側部分となります。
また、②について式変形すると、$$~~~3x+y+3≧0$$$$\hspace{ 48 pt}y≧-3x-3$$よって、②は直線 $y=-3x-3$ の上側部分となります。
この２つの領域の共通部分となるので、

この連立不等式の表す領域は、上の斜線部分となり、境界線を含みます。

問題解説(2)

問題次の不等式の表す領域を求めよ。$${\small (2)}~\biggl\{ \begin{eqnarray} ~y>-\frac{1}{2}x+1 \\ ~(x-2)^2+(y-1)^2>4 \end{eqnarray}$$

$$~~~\biggl\{ \begin{eqnarray} ~y>-\frac{1}{2}x+1 ~\cdots{\large ①}\\ ~(x-2)^2+(y-1)^2>4 ~\cdots{\large ②}\end{eqnarray}$$
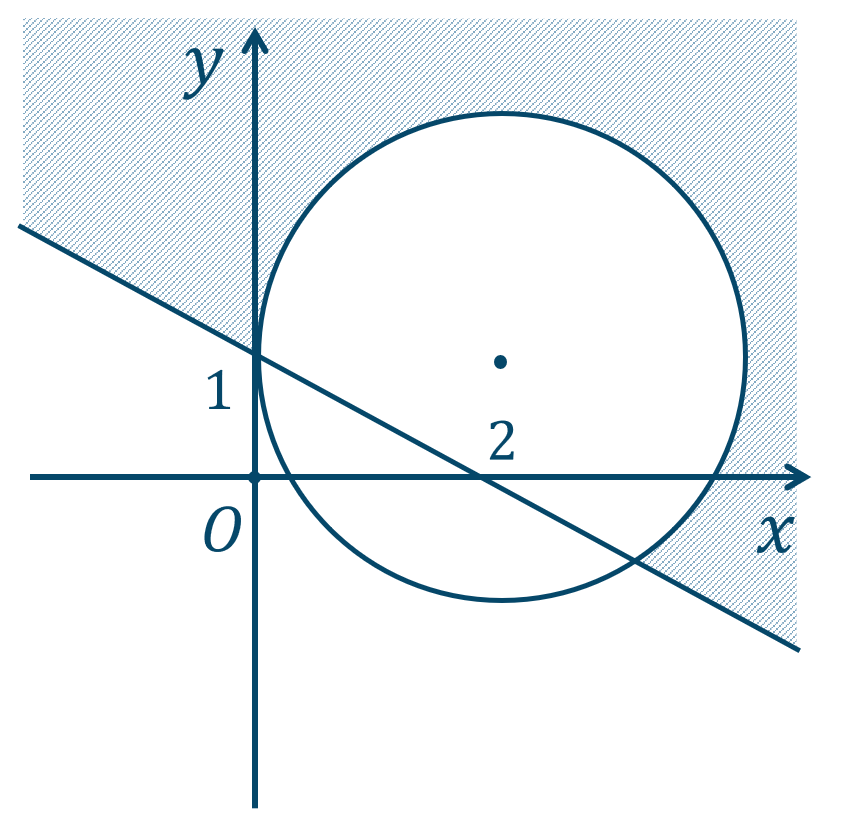
①は、直線 $y=-{\Large \frac{1}{2}}x+1$ の上側部分となります。
また、②は円 $(x-2)^2+(y-1)^2=4$ の外側部分となります。
この２つの領域の共通部分となるので、

この連立不等式の表す領域は、上の斜線部分となり、境界線を含みません。