線形計画法
① 与えられた不等式の表す領域を図示します。このとき、領域の頂点の座標を求めておきます。
② 最大値・最小値を求める式を \(=k\) とおき、図形で表します。
③ その図形が領域内に共有点をもつときの、\(k\) の最大値・最小値を求めます。
問題解説:線形計画法
$$~~~2x+3y-15≦0$$移項して、\(3\) で割ると、$$\hspace{ 10 pt}3y≦-2x+15$$$$\hspace{ 16 pt}y≦-\frac{2}{3}x+5~\cdots{\large ①}$$また、$$~~~4x+3y-21≦0$$移項して、\(3\) で割ると、$$\hspace{ 10 pt}3y≦-4x+21$$$$\hspace{ 16 pt}y≦-\frac{4}{3}x+7~\cdots{\large ②}$$
①は、直線 \(y=-{\Large \frac{2}{3}}x+5\) の下側部分となります。
②は、直線 \(y=-{\Large \frac{4}{3}}x+7\) の下側部分となります。
\(x≧0\) は、\(x=0\) の右側部分となります。
\(y≧0\) は、\(y=0\) の上側部分となります。
また、次の2直線の交点は、$$~~~\biggl\{ \begin{eqnarray} ~ 2x+3y-15=0~\cdots{\large ③} \\~4x+3y-21=0~\cdots{\large ④} \end{eqnarray}$$
④−③より、$$~~~(4x+3y-21)-(2x+3y-15)=0$$$$\hspace{ 25 pt}4x+3y-21-2x-3y+15=0$$$$\hspace{ 121 pt}2x-6=0$$移項して、\(2\) で割ると、$$\hspace{ 10 pt}2x=6$$$$\hspace{ 15 pt}x=3$$③に代入すると、$$~~~2\cdot3+3y-15=0$$$$\hspace{ 20 pt}6+3y-15=0$$$$\hspace{ 43 pt}3y-9=0$$移項して、\(3\) で割ると、$$\hspace{ 10 pt}3y=9$$$$\hspace{ 15 pt}y=3$$よって、この2直線の交点は \((3,3)\) となります。
また、③の直線と \(y\) 軸との交点は、\(x=0\) より、$$~~~2\cdot0+3y-15=0$$$$\hspace{ 38 pt}3y-15=0$$移項して、\(3\) で割ると、$$\hspace{ 10 pt}3y=15$$$$\hspace{ 15 pt}y=5$$よって、交点は \((0,5)\) となります。
また、④の直線と \(x\) 軸との交点は、\(y=0\) より、$$~~~4x+3\cdot0-21=0$$$$\hspace{ 38 pt}4x-21=0$$移項して、\(4\) で割ると、$$\hspace{ 10 pt}4x=21$$$$\hspace{ 15 pt}x=\frac{21}{4}$$よって、交点は \(\left( {\Large \frac{21}{4}}~,~0\right)\) となります。
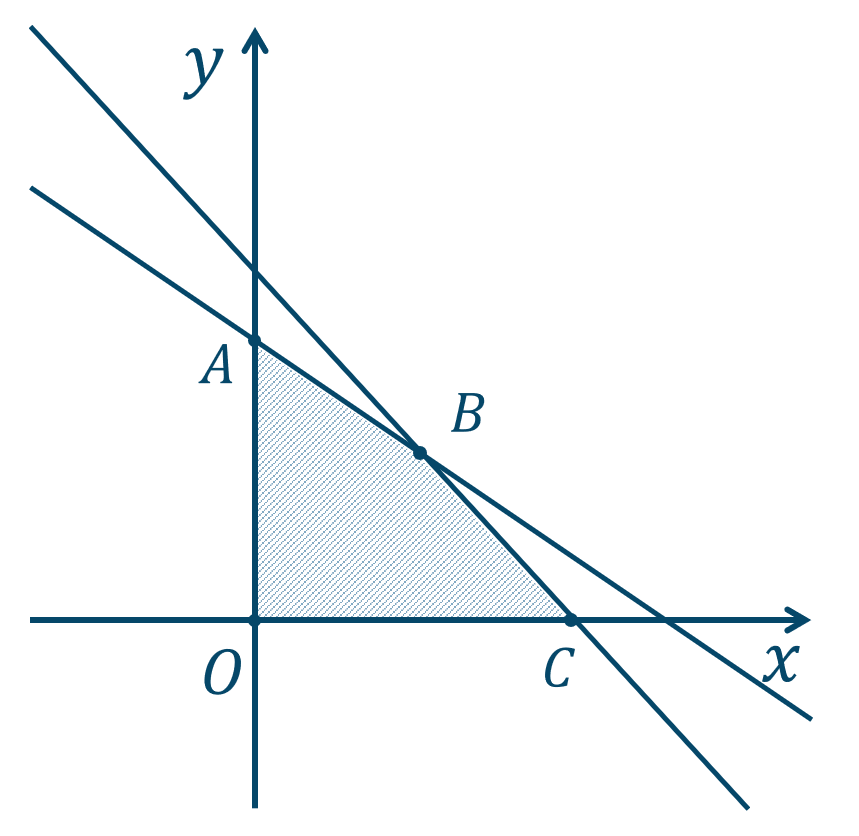
したがって、領域は
この図のように、4点 \(O(0,0)\) \(,\) \(A(0,5)\) \(,\) \(B(3,3)\) \(,\) \(C\left( {\Large \frac{21}{4}} ~,~0\right)\) を頂点とする四角形の内部および周となります。
次に、最大値・最小値を求める式を \(k\) を用いて表すと、$$~~~x+y=k$$$$\hspace{ 27 pt}y=-x+k$$よって、傾き \(-1\) で、\(y\) 切片が \(k\) の直線の方程式となります。
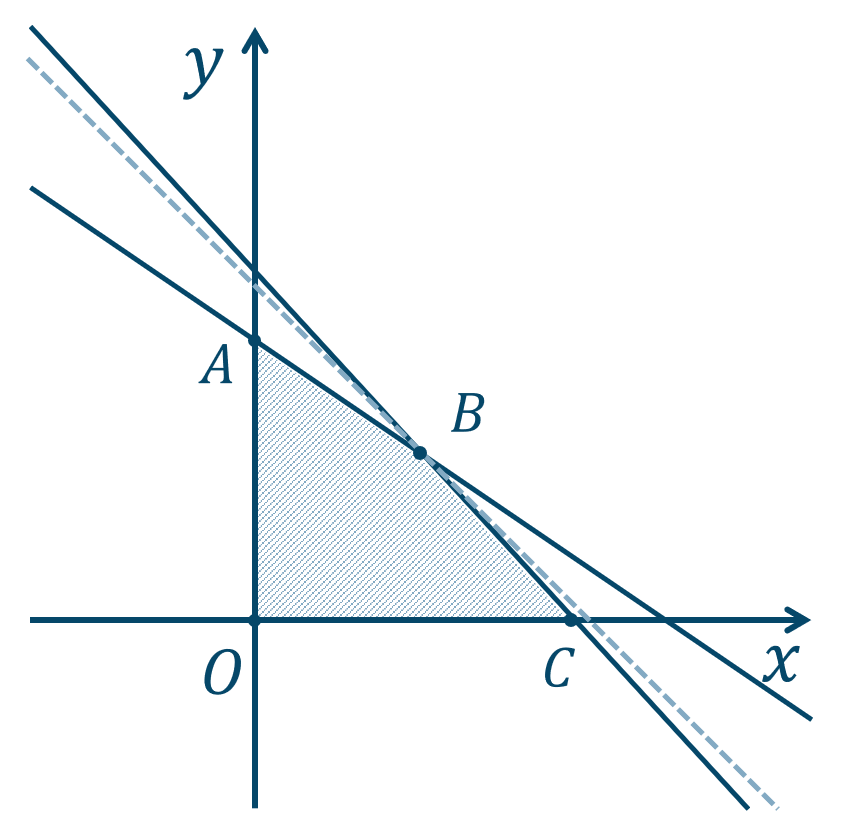
\(x,y\) が領域内を動くとき、\(k\) が最大となるのは、
図のときであり、点 \(B(3,3)\) を通るので、$$~~~k=3+3$$$$\hspace{ 16 pt}=6$$
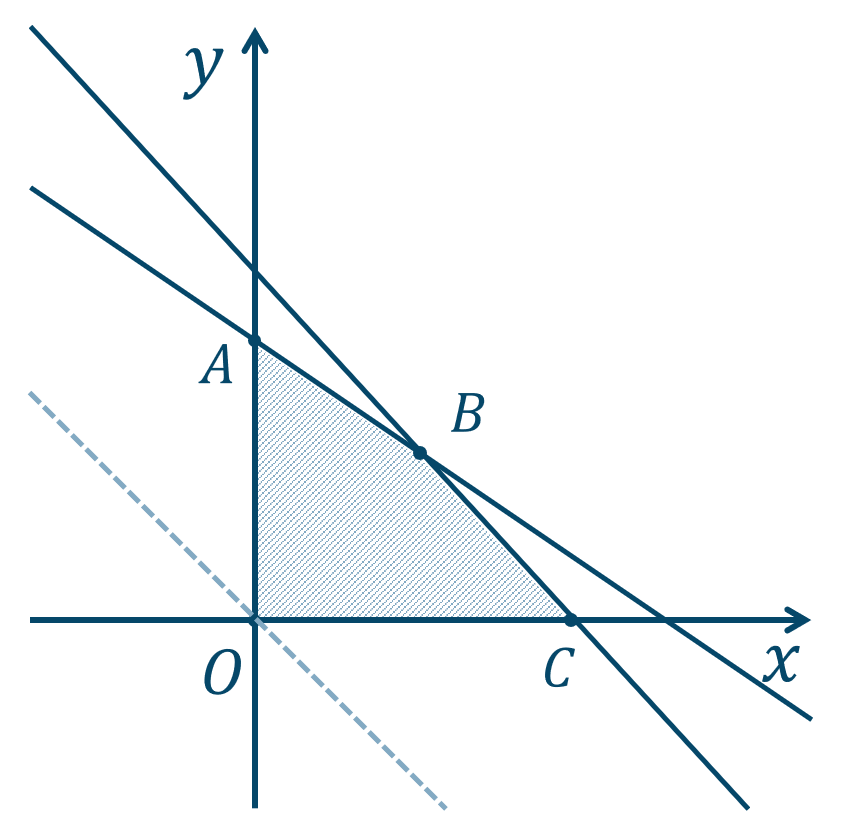
\(x,y\) が領域内を動くとき、\(k\) が最小となるのは、
図のときであり、点 \(O(0,0)\) を通るので、$$~~~k=0+0$$$$\hspace{ 16 pt}=0$$
以上より、答えは
\(x=3~,~y=3\) のとき最大値 \(6\)
\(x=0~,~y=0\) のとき最小値 \(0\)
となります。
今回のまとめ
線形計画法は手順が少し面倒ですが、よく出題されるので覚えておきましょう。領域を求めるとき、4つの頂点の座標を求めることを忘れないようにしましょう。