領域を用いた証明のやり方
Point：領域を用いた証明２つの不等式 \(P~,~Q\) について、
\(P\) ならば \(Q\)
この証明は、２つの不等式 \(P~,~Q\) の領域を図示して、\(P\) が \(Q\) の部分集合になっていれば命題が示されます。
\(P\) ならば \(Q\)
この証明は、２つの不等式 \(P~,~Q\) の領域を図示して、\(P\) が \(Q\) の部分集合になっていれば命題が示されます。
問題解説：領域を用いた証明
問題\(x^2+y^2<2\) ならば \(x^2+y^2-4y-12<0\) であることを証明せよ。
[証明]$$~P~:~x^2+y^2<2$$$$~Q~:~x^2+y^2-4y-12<0$$とすると、
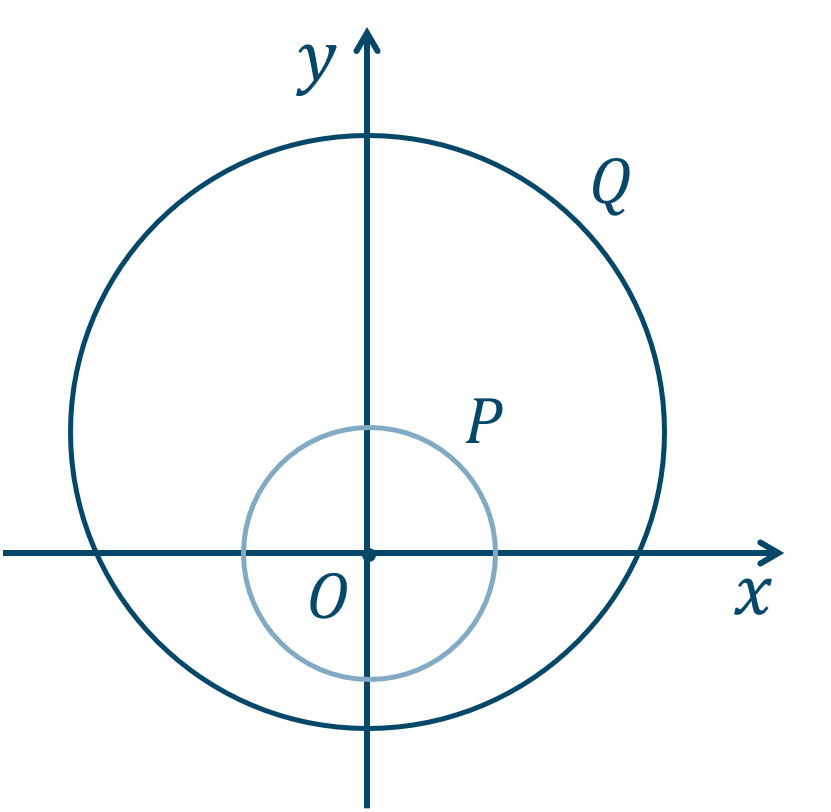
\(P\) は、\(x^2+y^2=2\) の内部となります。
\(Q\) について式変形すると、$$\hspace{ 10 pt}x^2+y^2-4y-12<0$$\(y\) について平方完成すると、$$\hspace{ 10 pt}x^2+(y^2-4y+4-4)-12<0$$$$\hspace{ 50 pt}x^2+(y-2)^2-16<0$$$$\hspace{ 72 pt}x^2+(y-2)^2<16$$よって、\(Q\) は円 \(x^2+(y-2)^2=16\) の内部となります。
よって、\(P~,~Q\) の表す領域を図示すると、
これより、\(P\subset Q\) となるので、
\(x^2+y^2<2\) ならば \(x^2+y^2-4y-12<0\)
が成り立ちます。[終]
今回のまとめ
２つの不等式の命題は、不等式の表す領域を用いて視覚的に証明できます。手順をしっかりと覚えておきましょう。
【問題一覧】数学Ⅱ：図形と方程式
このページは「高校数学Ⅱ：図形と方程式」の問題一覧ページとなります。解説の見たい単元名がわからないと...
yorikuwa.com
