集合の要素の個数の求め方
例えば、集合 \({\rm A}=\{~3~,~6~,~9~\}\) のとき、その要素の個数は
となります。
1〜50までの自然数について、3の倍数の個数を数えてみましょう。
はじめに \( 3\times n≦50 \) となるような最大の整数 \(n\) を見つけましょう。$$~~~n≦\frac{50}{3}=16.6 \cdots$$よって、\(n=16\) が最大の整数となります。
このことより、3の倍数の集合 \(\rm A\) は次のように表せます。
これより集合 \(\rm A\) の要素の個数は、\(n=1\) から \(n=16\) までの \(16\) 個あるので、\(n({\rm A})=16\) となります。
問題解説:集合の要素の個数
問題解説(1)
1〜100までの自然数のうち2の倍数の集合 \(\rm A\) について、 \( 2\times n≦100 \) となるような整数 \(n\) は、$$~~~n≦\frac{100}{2}=50$$よって、\(n=50\) が最大の整数となります。
このことより、集合 \(\rm A\) は次のように表せます。$$~~~{\rm A}=\{~2\times 1~,~2\times 2~,~\cdots~,~2\times 50~\}$$これより集合 \(\rm A\) の要素の個数は、\(n=1\) から \(n=50\) までの \(50\) 個あるので、\(n({\rm A})=50\) となります。
問題解説(2)
1〜100までの自然数のうち3の倍数の集合 \(\rm B\) について、\( 3\times n≦100 \) となるような整数 \(n\) は、$$~~~n≦\frac{100}{3}=33.3\cdots $$よって、\(n=33\) が最大の整数となります。
このことより、集合 \(\rm B\) は次のように表せます。$$~~~{\rm B}=\{~3\times 1~,~3\times 2~,~\cdots~,~3\times 33~\}$$これより集合 \(\rm B\) の要素の個数は、\(n=1\) から \(n=33\) までの \(33\) 個あるので、\(n({\rm B})=33\) となります。
問題解説(3)
\({\rm A} \cap {\rm B}\) は2の倍数かつ3の倍数であることより、6の倍数の集合を求めればよいことになります。
1〜100までの自然数のうち6の倍数の集合 \({\rm A} \cap {\rm B}\) について、\( 6\times n≦100 \) となるような整数 \(n\) は、$$~~~n≦\frac{100}{6}=16.6\cdots $$よって、\(n=16\) が最大の整数となります。
このことより、集合 \({\rm A} \cap {\rm B}\) は次のように表せます。$$~~~{\rm A} \cap {\rm B}=\{~6\times 1~,~6\times 2~,~\cdots~,~6\times 16~\}$$これより集合 \({\rm A} \cap {\rm B}\) の要素の個数は、\(n=1\) から \(n=50\) までの \(16\) 個あるので、\(n({\rm A} \cap {\rm B})=16\) となります。
問題解説(4)
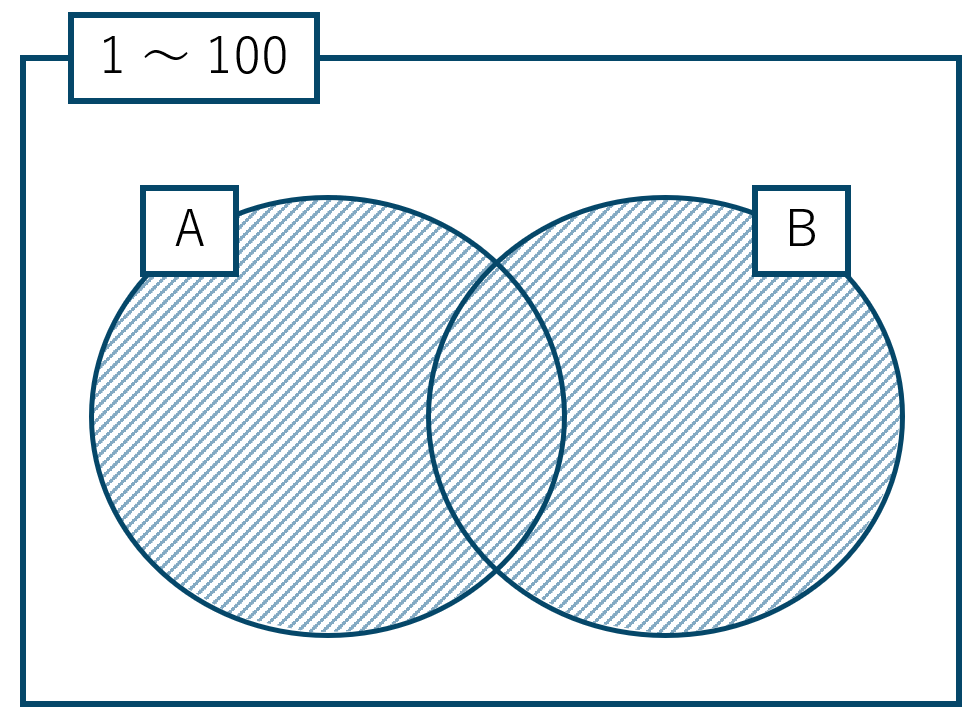
\({\rm A} \cup {\rm B}\) は2の倍数または3の倍数を表すので、ベン図は次のようになります。
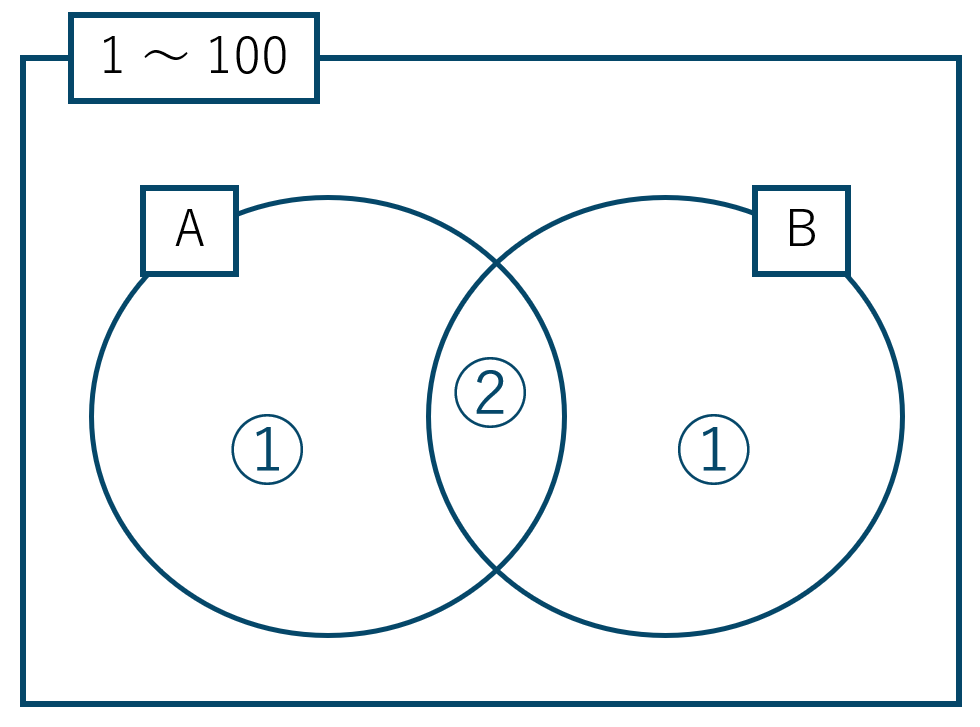
ここで、\(n({\rm A})+n({\rm B})\) の計算を考えると、
この図のように \(n({\rm A} \cap {\rm B})\) を2回カウントしていることになります。
よって、\(n({\rm A} \cap {\rm B})\) を1回分引く必要があるので、$$n({\rm A}\cup {\rm B})=n({\rm A})+n({\rm B})-n({\rm A} \cap {\rm B})$$が成り立ちます。
よって、$$~~~~~~50+33-16$$$$~=67$$答えは、\(n({\rm A} \cup {\rm B})=67\) となります。
今回のまとめ
集合の要素の個数の数え方について解説しました。「かつ」と「または」についてはその解法をしっかりとできるようになりましょう。