補集合の要素の個数

補集合の要素の個数とド・モルガンの法則
問題解説：
今回のまとめ

補集合の要素の個数とド・モルガンの法則

Point：補集合の要素の個数全体集合 $\rm U$ とその部分集合 $\rm A$ について、$\rm A$ でない集合を $ \overline {\rm A}$ で表し補集合といいます。

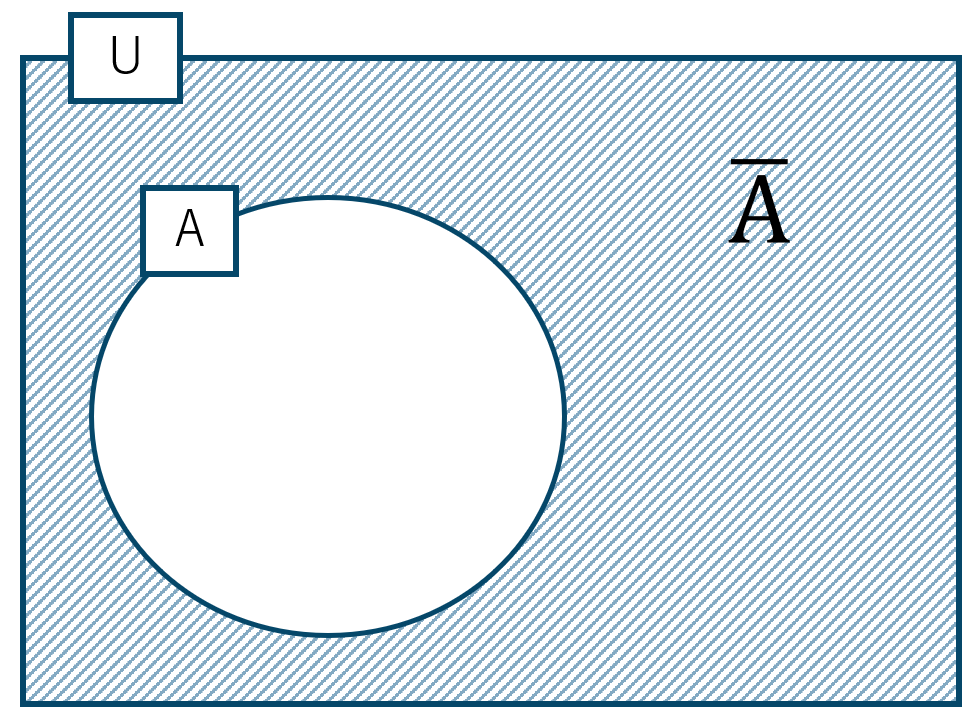
よって、補集合の要素の個数 $ n(\overline {\rm A}) $ は、全体集合の要素の個数を $ n({\rm U}) $ とするとき、

$$n(\overline {\rm A})=n({\rm U})-n({\rm A})$$

全体の個数から集合 $\rm A$ の要素の個数を引いて求めましょう。

Point：ド・モルガンの法則と要素の個数

全体集合 $\rm U$ とその部分集合 ${\rm A}~,~{\rm B}$ において、
$n( \overline {{\rm A}}) \cup n(\overline {{\rm B}} )$ をベン図で表すと、

この２つの和集合となるので、

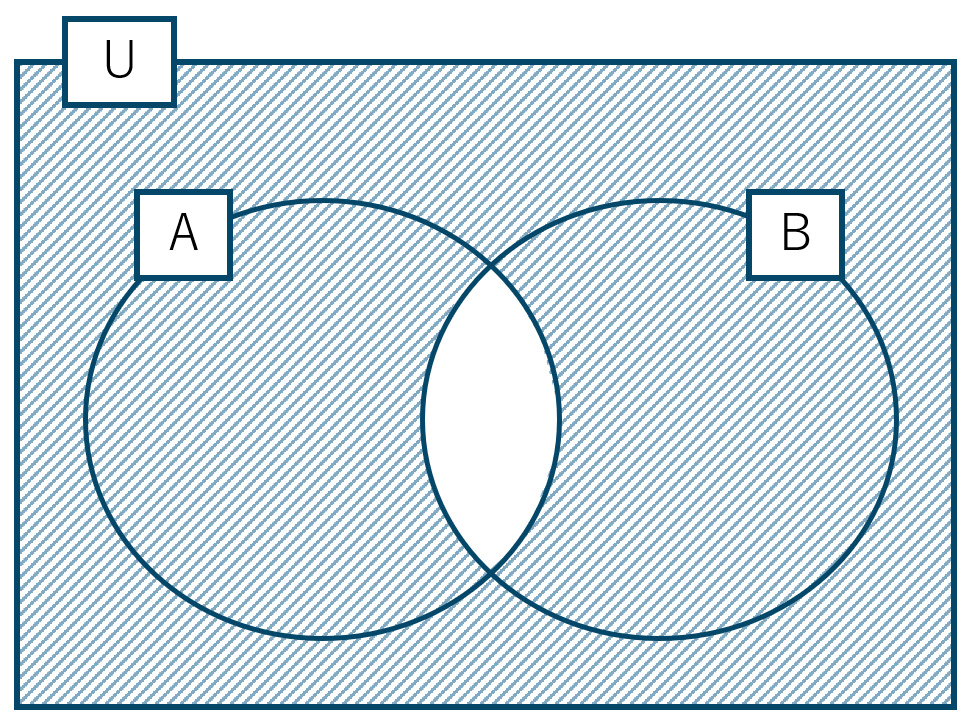
これは集合 $n( {\rm A}\cap {\rm B} )$ の補集合と同じになるので、

$$n(\overline {{\rm A} \cap {\rm B}})=n(\overline {{\rm A}} )\cup n(\overline {{\rm B}})$$

次に、$n( \overline {{\rm A}}) \cup n(\overline {{\rm B}} )$ をベン図で表すと、

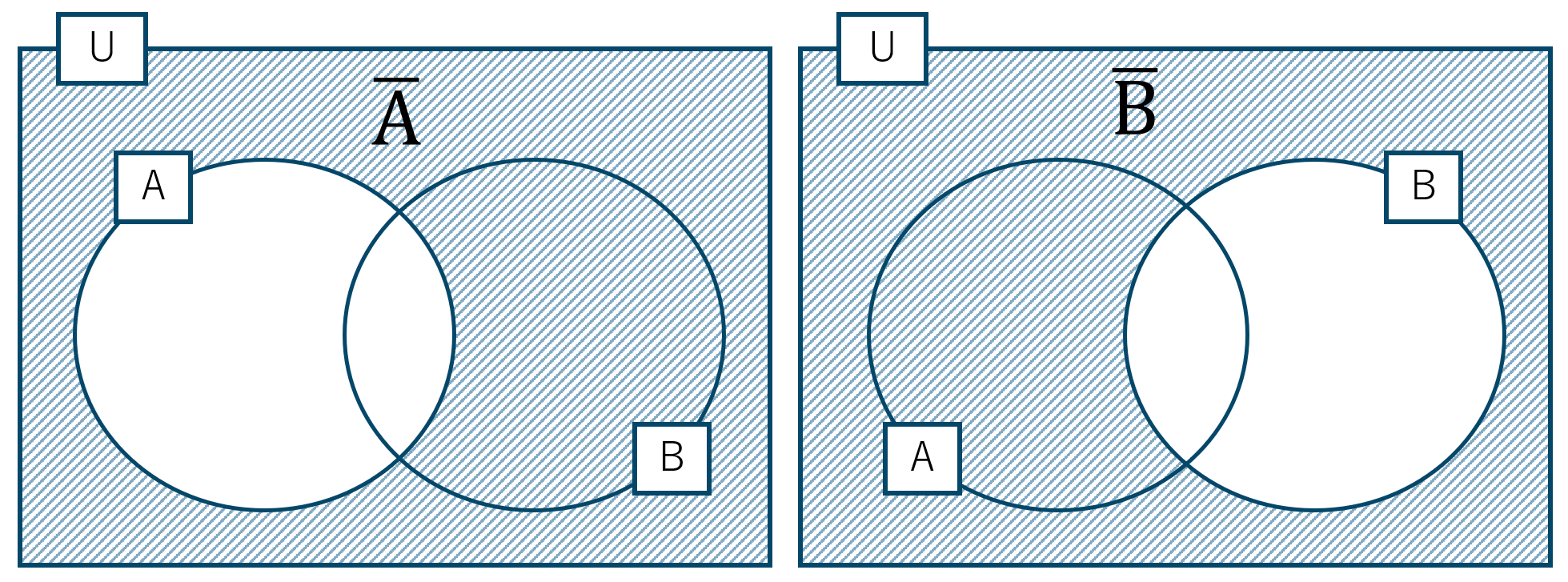
この２つの共通部分となるので、

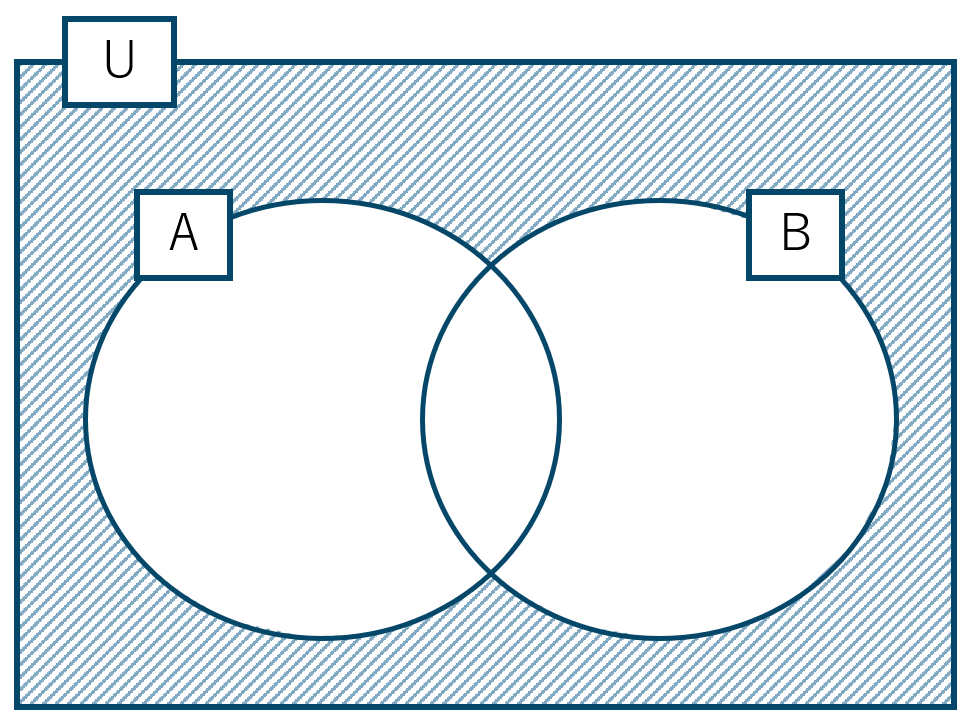
これは集合 $n( {\rm A} \cup {\rm B} )$ の補集合と同じになるので、

$$n(\overline {{\rm A} \cup {\rm B}})=n(\overline {{\rm A}} )\cap n(\overline {{\rm B}})$$

問題解説：

問題解説(1)

問題あるクラスの生徒 $40$ 人に数学と英語の好き・嫌いのアンケートを行った。数学が好きな生徒は $21$ 人、英語が好きな生徒は $17$ 人、どちらも好きな生徒は $8$ 人いた。このとき、次の生徒の人数を答えよ。
${\small (1)}~$数学が嫌いな生徒

問題に入る前に集合の要素の個数をまとめておきましょう。
クラス全体の集合を $\rm U$ とすると、$$~~~n({\rm U})=40$$数学が好きな生徒の集合を $\rm A$、英語が好きな生徒の集合を $\rm B$ とすると、$$~~~n({\rm A})=21~,~n({\rm B})=17$$また、どちらも好きな生徒の集合を ${\rm A} \cap {\rm B}$ とすると、$$~~~n({\rm A} \cap {\rm B})=8$$それでは問題を見ていきましょう。

数学を嫌いな生徒の数は $ n(\overline {\rm A}) $ と表されて、ベン図は次のようになります。

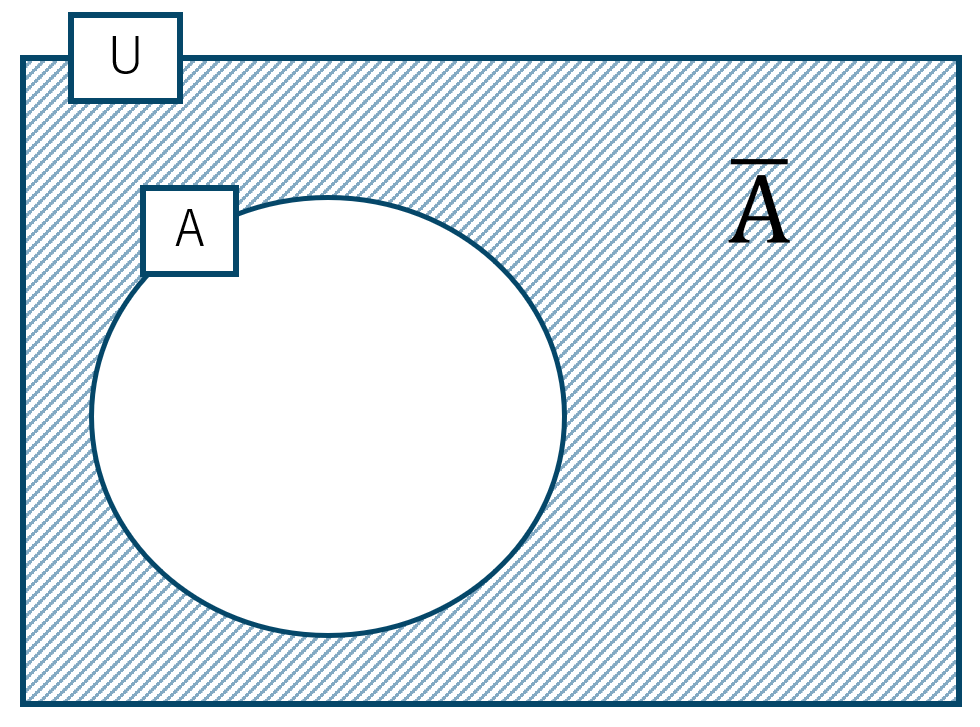
よって、$$~~~n(\overline {\rm A})=n({\rm U})-n({\rm A})$$$$\hspace{32pt}=40-21=19$$答えは $ n(\overline {\rm A})=19 $ となります。

問題解説(2)

問題あるクラスの生徒 $40$ 人に数学と英語の好き・嫌いのアンケートを行った。数学が好きな生徒は $21$ 人、英語が好きな生徒は $17$ 人、どちらも好きな生徒は $8$ 人いた。このとき、次の生徒の人数を答えよ。
${\small (2)}~$数学が嫌いで英語が好きな生徒

数学が嫌いで英語が好きな生徒の数は $ n(\overline {\rm A}\cap {\rm B} ) $ と表されて、ベン図は次のようになります。

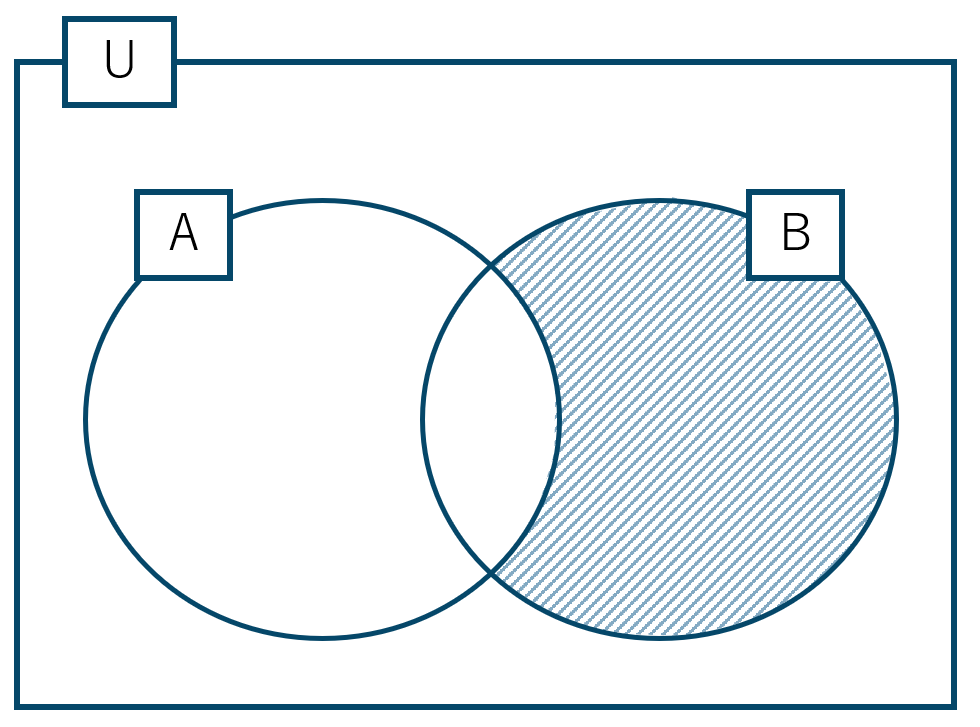
これより、$n({\rm B})$ から $n({\rm A}\cap {\rm B})$ を引けばよいので、$$~~~n(\overline {\rm A}\cap {\rm B} )=n({\rm B})-n({\rm A}\cap {\rm B})$$$$\hspace{50pt}=17-8=9$$答えは $ n(\overline {\rm A}\cap {\rm B} )=9 $ となります。

問題解説(3)

問題あるクラスの生徒 $40$ 人に数学と英語の好き・嫌いのアンケートを行った。数学が好きな生徒は $21$ 人、英語が好きな生徒は $17$ 人、どちらも好きな生徒は $8$ 人いた。このとき、次の生徒の人数を答えよ。
${\small (3)}~$数学と英語の少なくとも一方が好きな生徒

数学と英語の少なくとも一方が好きな生徒の数は、数学が好きまたは英語が好きとなるので $n({\rm A} \cup {\rm B})$ と表されてベン図は次のようになります。

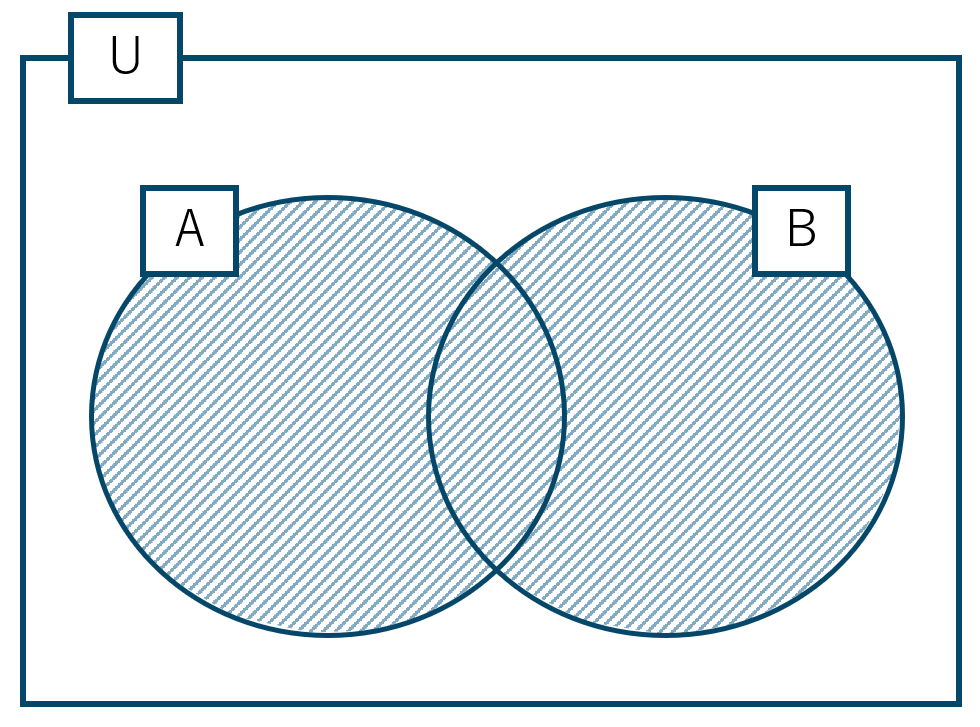
これより、$n({\rm A})$ と $n({\rm B})$ を合わせたものから $n({\rm A}\cap {\rm B})$ を１回引けばよいので、$$~~~n({\rm A} \cup {\rm B})=n({\rm A})+n({\rm B})-n({\rm A} \cap {\rm B})$$$$\hspace{50pt}=21+17-8=30$$答えは $n({\rm A} \cup {\rm B})=30$ となります。

問題解説(4)

問題あるクラスの生徒 $40$ 人に数学と英語の好き・嫌いのアンケートを行った。数学が好きな生徒は $21$ 人、英語が好きな生徒は $17$ 人、どちらも好きな生徒は $8$ 人いた。このとき、次の生徒の人数を答えよ。
${\small (4)}~$数学と英語のどちらも嫌いな生徒

数学と英語のどちらも好きでない生徒の数は $ n(\overline {\rm A}\cap \overline {\rm B} ) $ で表される。
ド・モルガンの法則より、$$~~~ n(\overline {\rm A}\cap \overline {\rm B})= n(\overline{ {\rm A}\cup {\rm B}})$$となり、またベン図は次のようになります。

よって、$$~~~n(\overline{ {\rm A}\cup {\rm B}})=n({\rm U})-n({\rm A} \cup {\rm B})$$(3)の答え $n({\rm A} \cup {\rm B})=30$ より、$$\hspace{50pt}=40-30=10$$答えは $ n(\overline {\rm A}\cap \overline {\rm B} )=10 $ となります。