文字の順列の解法
① 並べる文字の数だけ箱を描きます。
② 左の箱から順に、文字の入れる場合の数を書き込みます。
③ 積の法則より、場合の数を求めます。
・隣り合う文字がある場合
① 隣り合う文字を1つのセットと考えて、残りの文字との順列を考えます。
② セットにした中での順列を考えます。
③ 積の法則より、場合の数を求めます。
・特定の文字が両端にくる場合
① 特定の文字が両端にくる場合の数を求めます。
② 残りの文字を間の部分に並べる順列を考えます。
③ 積の法則より、場合の数を求めます。
問題解説:文字の順列
問題解説(1)
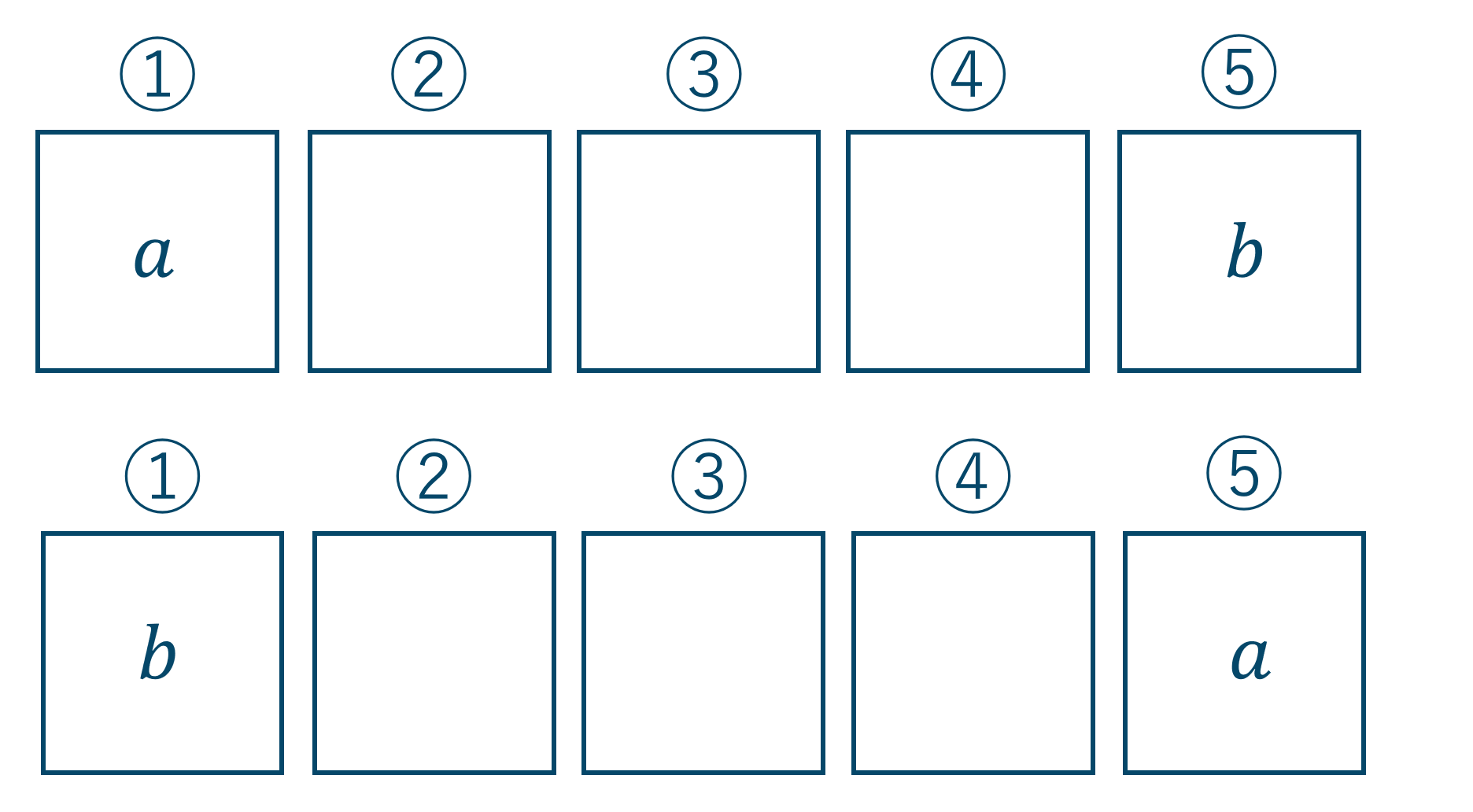
\({\small (1)}~\)\(a,b\) が隣り合う並べ方
\(a,b\)が隣り合うのでこれを1つのセットとします。
この1つのセットと残りの3文字の合計4つのものの順列は、
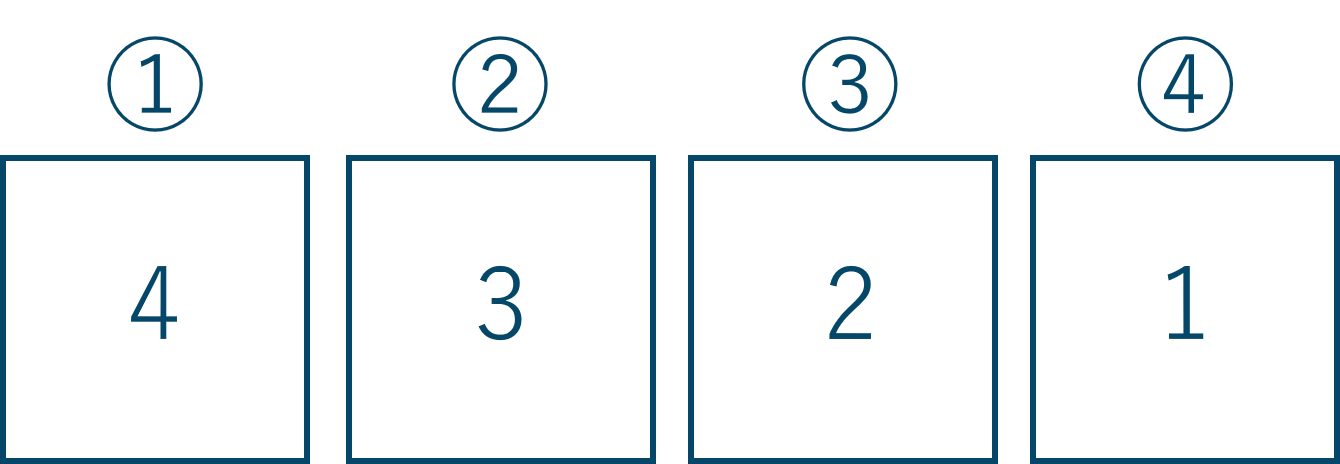
4つの箱を描いて、左から順に文字の入り方の場合の数を考えると、
①の箱には1セットと残りの3文字で4通り
②の箱には①で選ばなかった3通り
③では①と②で選ばなかった2通り
④では残った1通り
したがって、計算式は$$~~~4\times 3\times 2\times 1 = 24$$よって、24通りとなります。
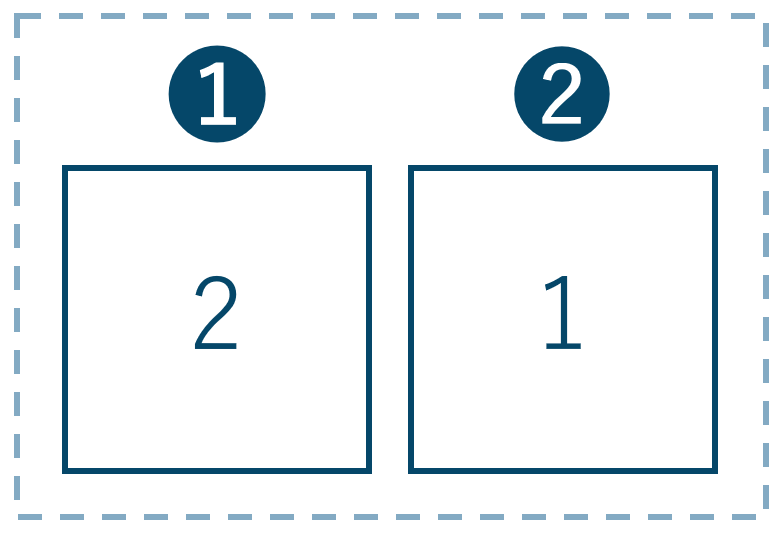
次にセットとした中でも順列を考えると、
➊には \(a,b\) のどちらか一方で1通り
❷には➊で選ばなかった方で1通り
計算式は、$$~~~2\times 1=2$$よって、2通りとなります。
以上より、この2つの場合の数は「連続して起きている」ので積の法則より$$~~~24\times 2=48$$答えは、48通りとなります。
問題解説(2)
\({\small (2)}~\)\(a,b\) が両端にくる並べ方
両端が特定の文字になるパターンです。\(a,b\)が両端にくるので、初めに両端の文字 \(a,b\) の入り方を考えましょう。
これより、\(a,b\) の入り方は2通りとなります。
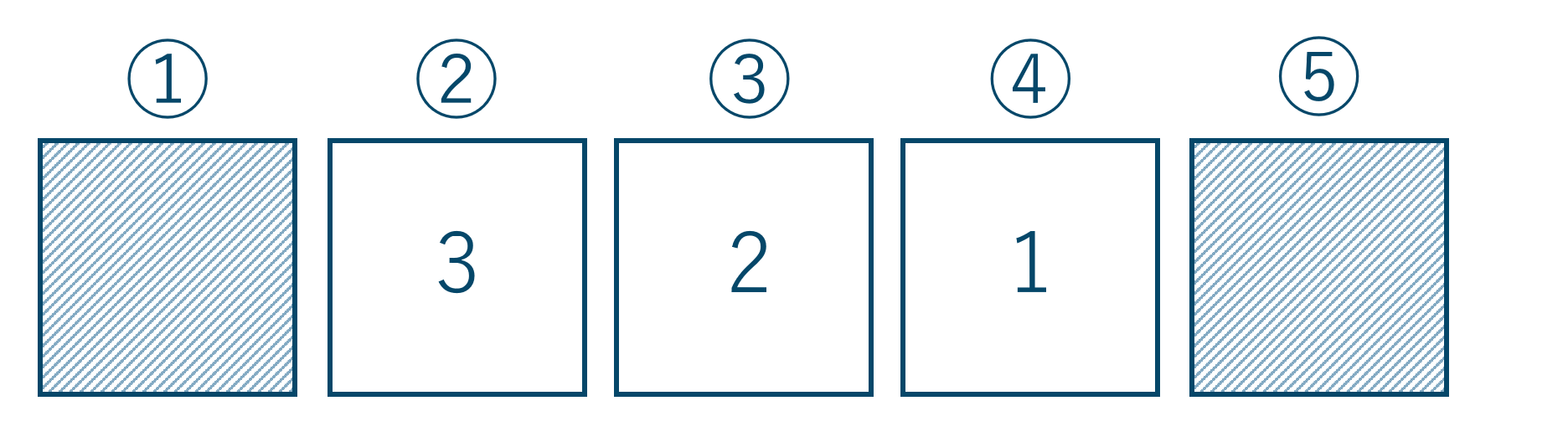
また、この間に入る残りの3文字の順列は3つの箱を描いて、左から順に入り方の場合の数を考えると
②の箱には \(c,d,e\) から1つ選ぶので3通り
③の箱には②で選ばなかった2通り
④の箱には残った1通り
したがって、計算式は、$$~~~3\times 2\times 1=6$$よって6通りなります。
以上より、この2つの場合の数は「連続して起きている」ので積の法則より$$~~~2\times 6=12$$答えは、12通りとなります。
今回のまとめ
順列の問題は公式だけでは解けません。今回のように条件が付くようなパターンでは「箱を描いて、順番に場合の数を考える」方法が非常に重要となります。この2つのパターンは条件付きの順列の基本となる問題です。条件に合った解法をしっかりと理解しできるようになりましょう!