数字の順列の解法
① 並べる数字の桁数だけ箱を描きます。
② 左の桁から順に、数字の入れる場合の数を書き込みます。
③ 積の法則より、場合の数を求めます。
整数を作る場合は、先頭の位に \(0\) が入れないことに注意して場合の数を求めましょう。
問題解説:数字の順列
問題解説(1)
\({\small (1)}~\)3桁の整数
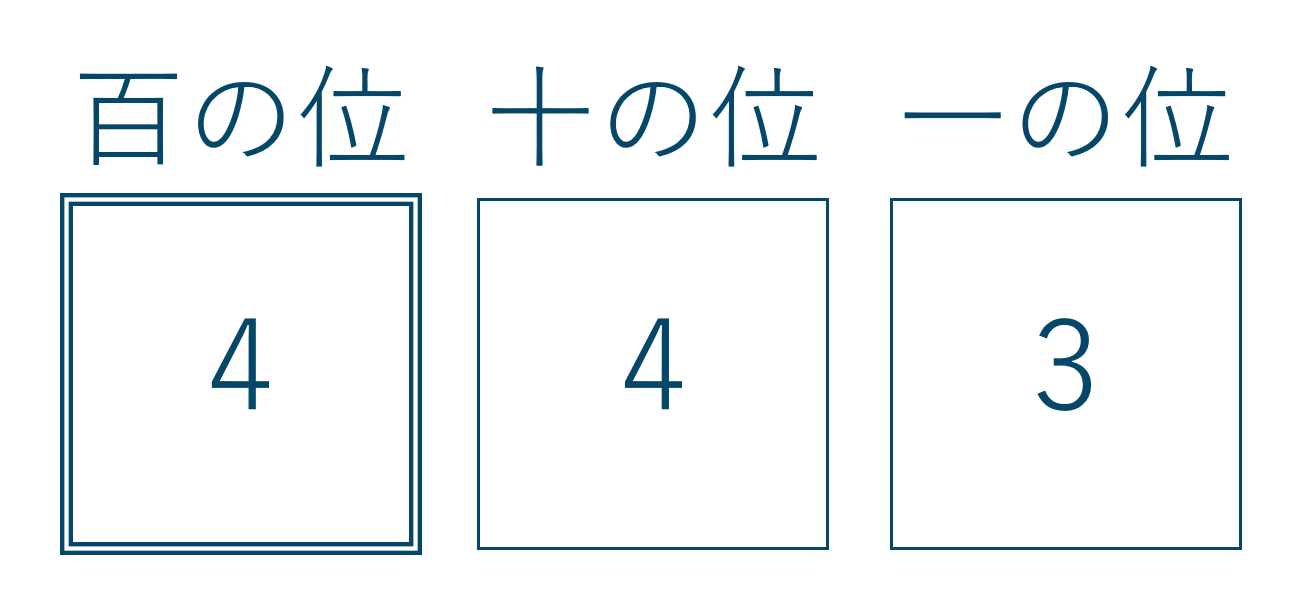
3桁の整数を作るので百の位、十の位、一の位の箱を描いて、数字の入り方の場合の数を百の位から考えます。
百の位には0以外から選ばれるので4通り
十の位は、百の位で入れた数字以外と0から選ばれるので4通り
一の位には残りの3つの数字から選ばれるので3通り
計算式は、$$~~~4 \times 4 \times 3 =48$$よって、答えは48通りとなります。
問題解説(2)
\({\small (2)}~\)3桁の暗証番号
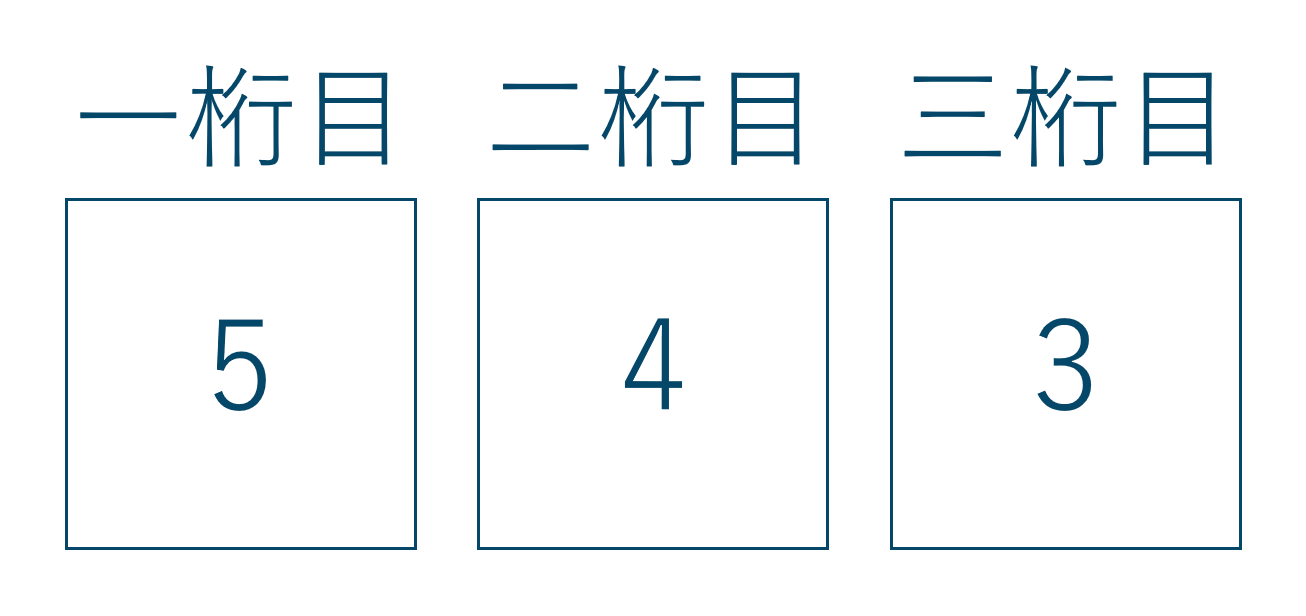
暗証番号は整数と違って、先頭の位に0が使えます。ですので単純に1桁目、2桁目、3桁目と箱を描き、それぞれの場合の数を書き並べましょう。
1桁目にはすべての数字より5通り
2桁目には1桁目に入れた数字以外の数字より4通り
3桁目には残りの3つの数字より3通り
計算式は、$$~~~5 \times 4 \times 3 =60$$よって、答えは60通りとなります。
問題解説(3)
\({\small (3)}~\)3桁の偶数
偶数となるためには一の位が偶数または0となるときです。それらを場合分けをして考えますが、0は百の位には入れないので0が一の位に入るかどうかで場合分けが必要となります。よって、「一の位が偶数」と「一の位が0」で分けましょう。
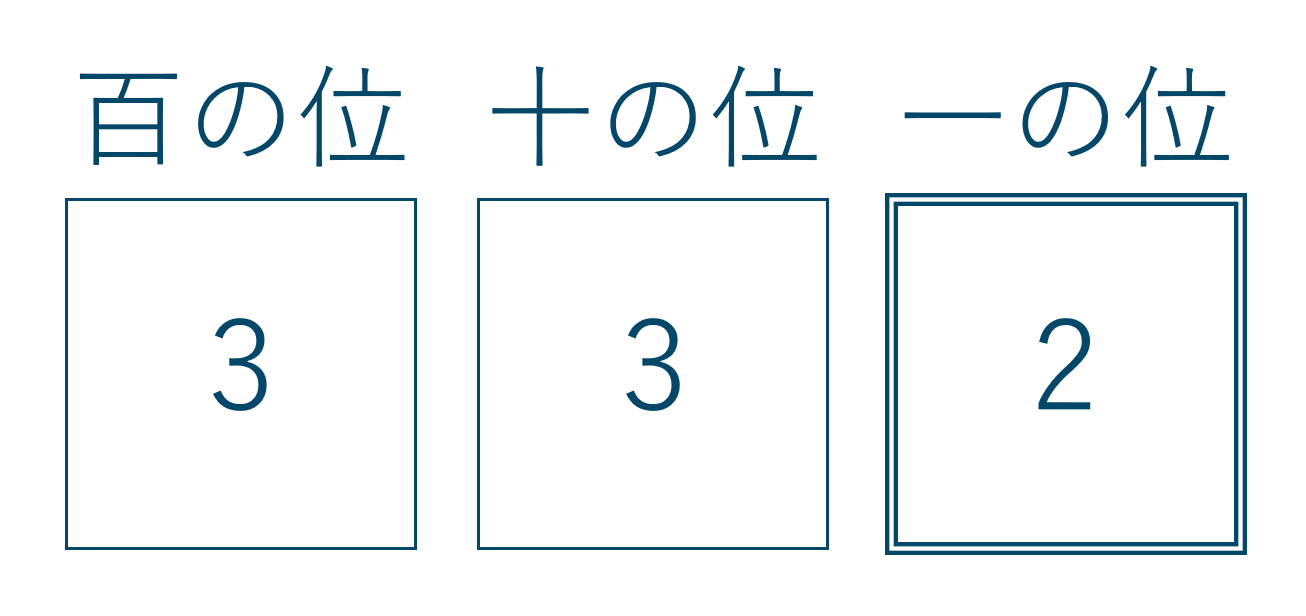
(ⅰ) 一の位が偶数の場合
一の位に入る数字は2または4なので2通り
百の位には一の位で選ばれなかった数字と残りの0以外の数字が入れるので3通り
十の位は残り数字から入れるので3通り
計算式は、$$~~~3 \times 3 \times 2 =18$$よって、18通りとなります。
(ⅱ) 一の位が0の場合
一の位は0で固定なので1通り
百の位は0以外の4つの数字から選ばれるので4通り
十の位は残りの3つの数字から選ばれ3通り
計算式は、$$~~~1 \times 4 \times 3 =12$$よって、12通りとなります。
ここで、(ⅰ)と(ⅱ)は「同時に起こらない」ので和の法則より計算式は、$$~~~18 + 12 =30$$よって、答えは30通りとなります。
問題解説(4)
\({\small (4)}~\)3桁の整数のうち、300以上の整数
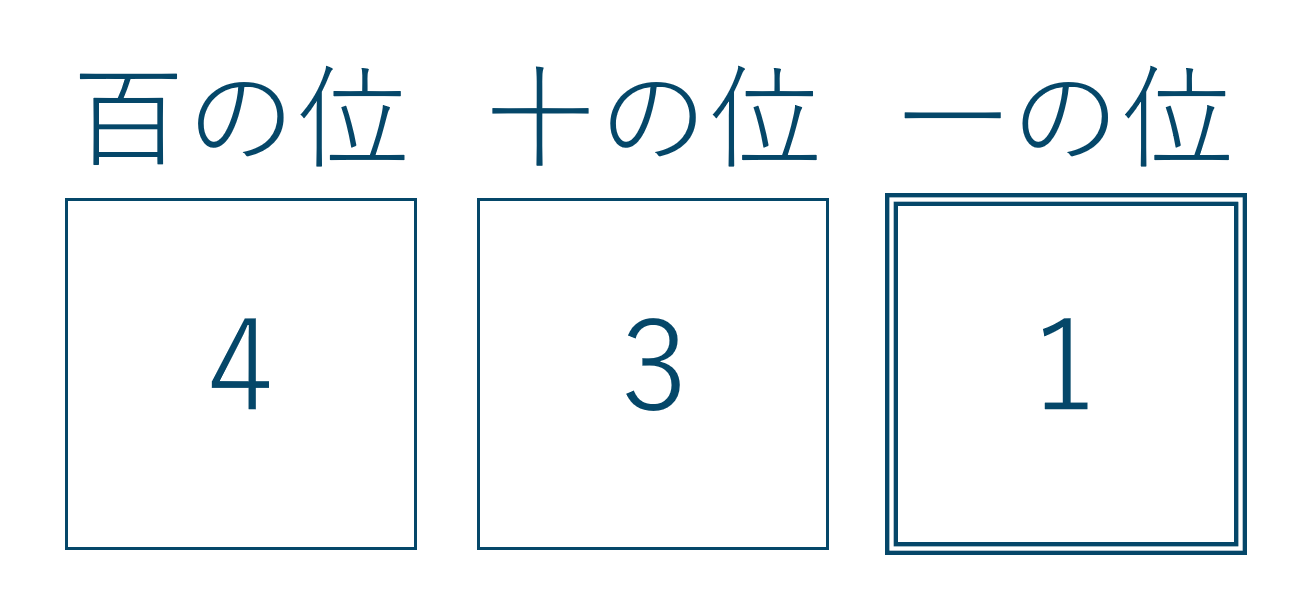
3桁の整数で300以上の整数を作るので、百の位は3または4でないといけません。百の位、十の位、一の位の箱を描いて考えましょう。
百の位は3または4で2通り
十の位は百の位で選ばれなかった数字と残りの数字が選択肢となるので4通り
一の位は残りの3つの数字から選ばれるので3通り
計算式は、$$~~~2 \times 4 \times 3 =24$$よって答えは24通りとなります。
今回のまとめ
順列の問題は記号を単純に使うだけでは解けません。このような問題は箱を描いて1つずつ箱に入れる場合の数を考えていきましょう。また、整数を作るときには先頭の位に0が入らないことに注意して計算しましょう。