円順列とじゅず順列の解法
Point:円順列例題1:5つの文字 \( a,b,c,d,e \) を円形に並べるときの場合の数を求めよ。
・解法パターン1
順列ですので、箱を描いて考えましょう。円形に①〜⑤と描いて、場合の数を書いて積の法則を使うのですが、このままでは回転したときのダブりが出てしまいます。

この5つは回転したときに全く同じになるので1つの場合の数と考える必要があります。
回転したときのダブりが出ないように「特定のものを一か所に固定する」ことをします。
この例題では \( a \) を①の場所に固定します。

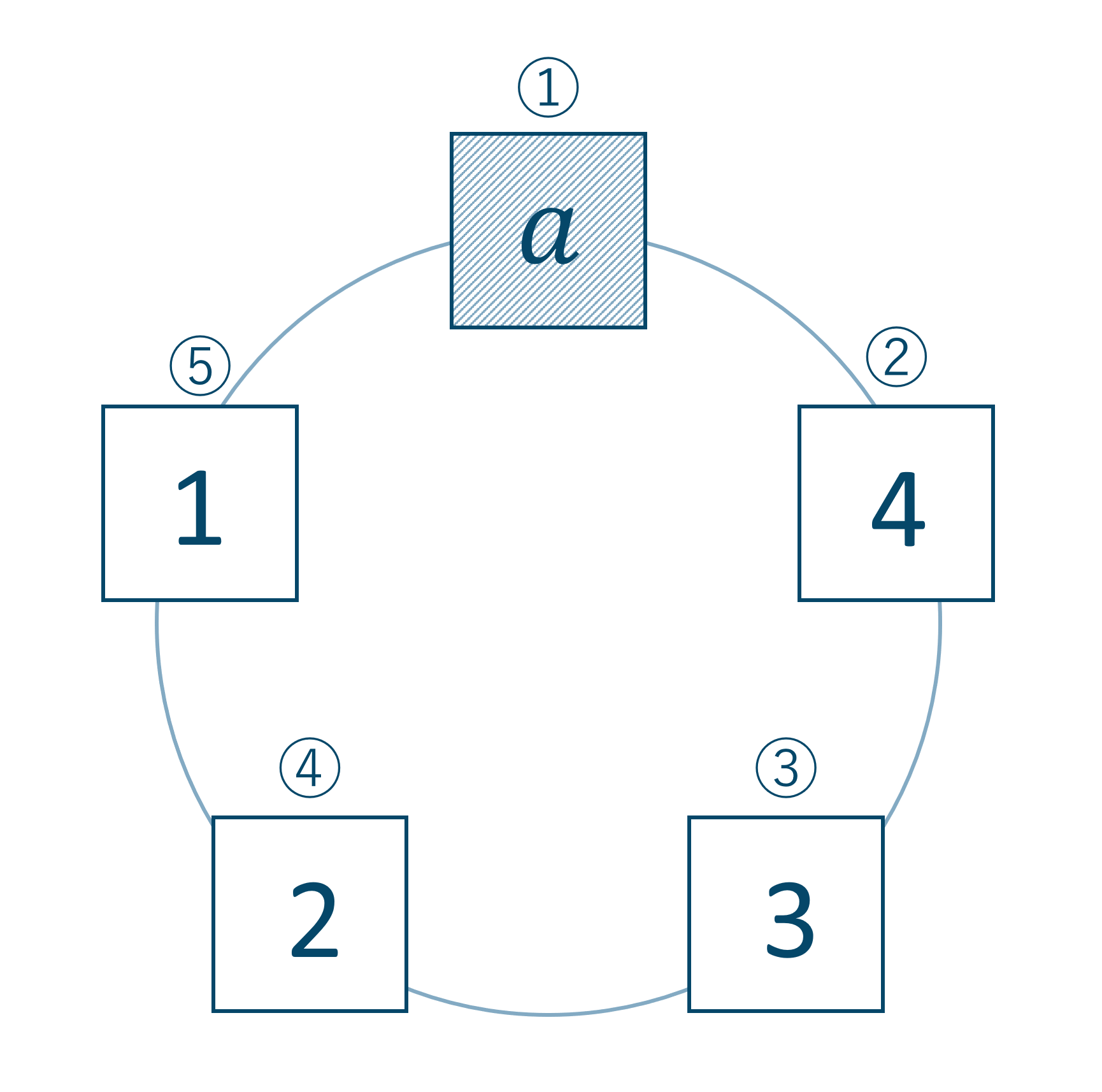
すると回転したときのダブりが出てこなくなり場合の数が求まります。固定された \( a \) 以外の文字を②~⑤に入れていけばよいので、計算式は$$~~~(5-1)!=4\times 3\times 2\times 1=24$$となり求める場合の数は24通りとなる。
このように円順列は (並べるものの数−1)!と計算できます。
・解法パターン2
箱を描いて、場合の数を書くと回転によるダブりは以下のようになります。


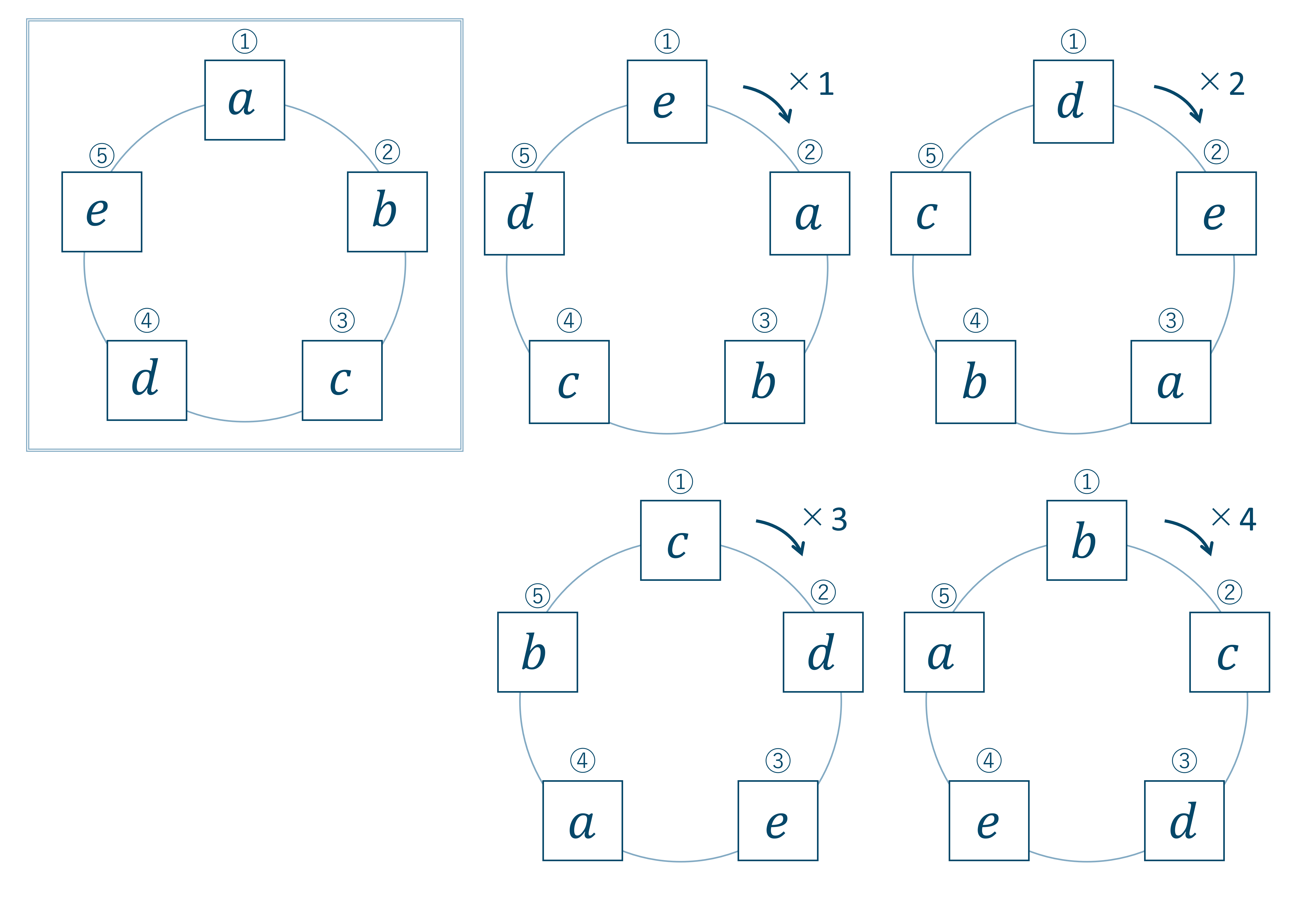
これより、回転によるダブりは1つの場合の数に対して「並べるものの数」通り発生します。今回は時計回りに\( a,b,c,d,e \)となるのは5通りのダブりが発生しています。
よって通常の順列と同じようにと計算し、円順列と考えたときそれぞれ通りダブりが出てくるのを考慮し計算しましょう。$$~~~5! \div 5=4\times 3\times 2\times 1 =24$$よって、答えは24通りとなります。
まとめると、(並べるものの数)!÷ (並べるものの数) と計算できます。
・解法パターン1
順列ですので、箱を描いて考えましょう。円形に①〜⑤と描いて、場合の数を書いて積の法則を使うのですが、このままでは回転したときのダブりが出てしまいます。

この5つは回転したときに全く同じになるので1つの場合の数と考える必要があります。
回転したときのダブりが出ないように「特定のものを一か所に固定する」ことをします。
この例題では \( a \) を①の場所に固定します。


すると回転したときのダブりが出てこなくなり場合の数が求まります。固定された \( a \) 以外の文字を②~⑤に入れていけばよいので、計算式は$$~~~(5-1)!=4\times 3\times 2\times 1=24$$となり求める場合の数は24通りとなる。
このように円順列は (並べるものの数−1)!と計算できます。
・解法パターン2
箱を描いて、場合の数を書くと回転によるダブりは以下のようになります。



これより、回転によるダブりは1つの場合の数に対して「並べるものの数」通り発生します。今回は時計回りに\( a,b,c,d,e \)となるのは5通りのダブりが発生しています。
よって通常の順列と同じようにと計算し、円順列と考えたときそれぞれ通りダブりが出てくるのを考慮し計算しましょう。$$~~~5! \div 5=4\times 3\times 2\times 1 =24$$よって、答えは24通りとなります。
まとめると、(並べるものの数)!÷ (並べるものの数) と計算できます。
Point:じゅず順列
じゅず順列では、表裏でダブりが出るので次の手順で解きましょう。
例題2:5つの文字\( a,b,c,d,e \)が入った球を用いてじゅずを作るときの場合の数を求めよ。
じゅず順列は円形に並べるまでは円順列と同じですが、じゅずやブレスレットを作るので表裏があります。
具体的には次の2つの場合の数は円順列のときは別としてカウントしていましたが、じゅず順列では裏から見たとき同じ並び方となるので、この2つは同じものとしてカウントします。
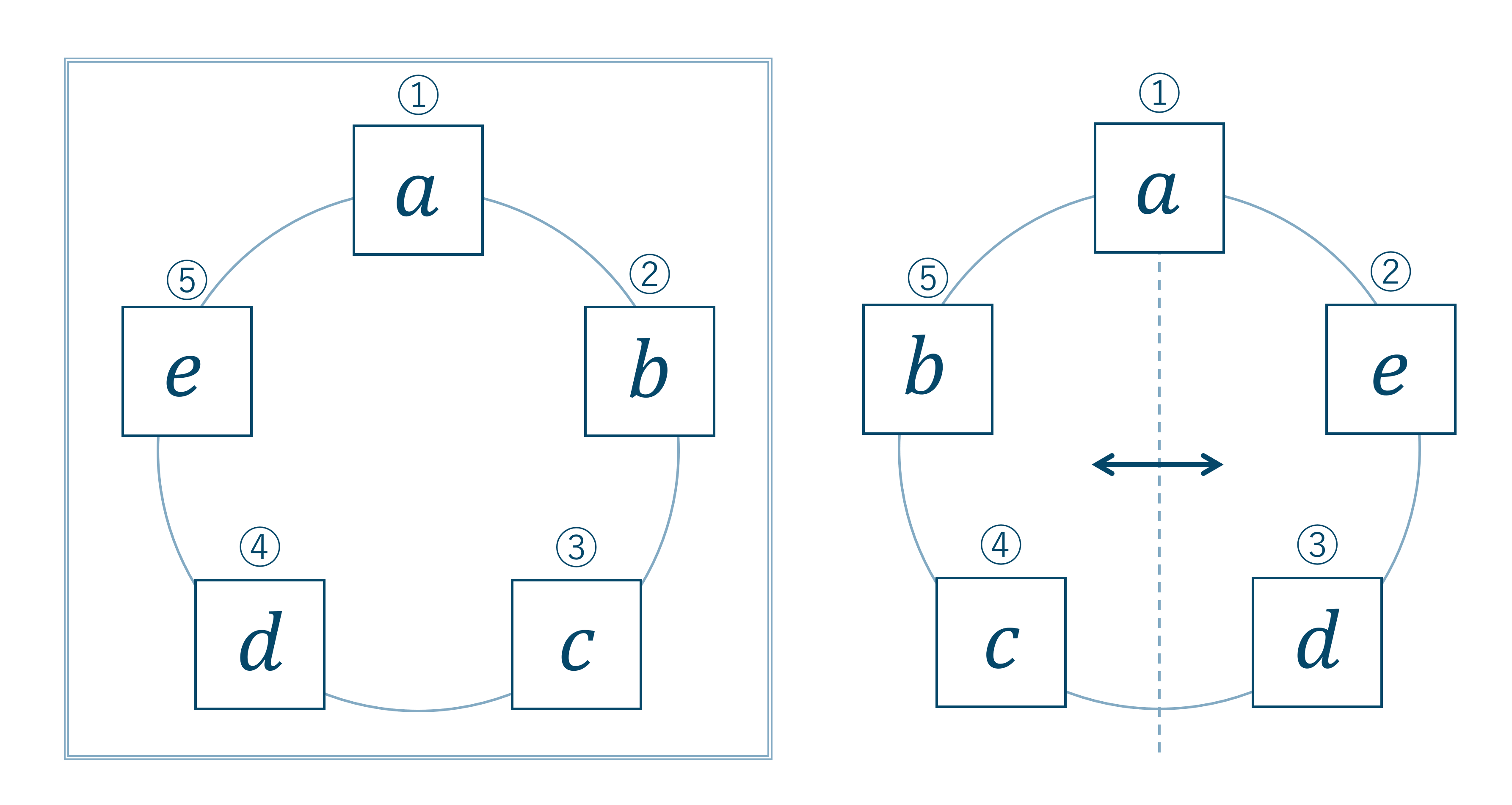
また、円順列として考えたすべての通りについてこの表裏の2通りのダブりが存在することになります。
よって、この例題での計算は、$$~~~(5-1)!=4\times 3\times 2\times 1=24$$$$~~~24 \div 2=12$$答えは12通りとなります。
このように、全ての通りで表裏の2通りのダブりがでるので(円順列として計算)÷2を計算する必要があります。
問題解説:円順列とじゅず順列
問題解説(1)
問題8種類の球を用いて次の場合の数を求めよ。
\({\small (1)}~\)円状に並べる方法
\({\small (1)}~\)円状に並べる方法
解法パターン1を使って計算すると$$~~~(8-1)!=7!=5040$$よって、答えは5040通りとなります。
また、解法パターン2を使うと、$$~~~8! \div 8=7!=5040$$よって、答えは5040通りとなります。
問題解説(2)
問題8種類の球を用いて次の場合の数を求めよ。
\({\small (2)}~\)じゅずを作るときの方法
\({\small (2)}~\)じゅずを作るときの方法
8つのものの円順列を考えると、$$~~~(8-1)!=7!=5040$$じゅず順列にするので表裏のダブりを考えて計算すると、$$~~~5040 \div 2=2520$$よって、答えは2520通りとなります。
今回のまとめ
このように順列の計算パターンで円順列とじゅず順列は回転や表裏のダブりをなくす計算が必要となります。それぞの解法を計算の意味を理解しつつ覚えておきましょう。


【問題一覧】数学A:場合の数と確率
このページは「高校数学A:場合の数と確率」の問題一覧ページとなります。解説の見たい単元名がわからない...


