条件付き円順列
この特定の \(n\) 人を1つのグループと考えて固定して、残りの人の順列を考えます。
次にこのグループの中での順列を考えて、積の法則より場合の数を求めます。
( \(n\) 人以外の順列)×( \(n\) 人グループの順列)
(2) 特定の2人が向い合うとき
この特定の2人を固定して、残りの人の順列を考えます。
このとき、特定の2人は入れ替えたら回転させると入れ替える前と同じになります。よって、特定の2人の入れ替えは考えなくてよくなります。
(特定の2人以外を並べる順列)×1
問題解説:条件付き円順列
問題解説(1)
\({\small (1)}~\)すべての座り方
先生と生徒合わせて6人が円形のテーブルに座ることになります。
前回の解法パターン1を使って計算すると$$~~~(6-1)!=5!=120$$よって、答えは120通りとなります。
また、前回の解法パターン2を使うと、$$~~~6! \div 6=5!=120$$よって、答えは120通りとなります。
問題解説(2)
\({\small (2)}~\)先生2人が隣り合う座り方
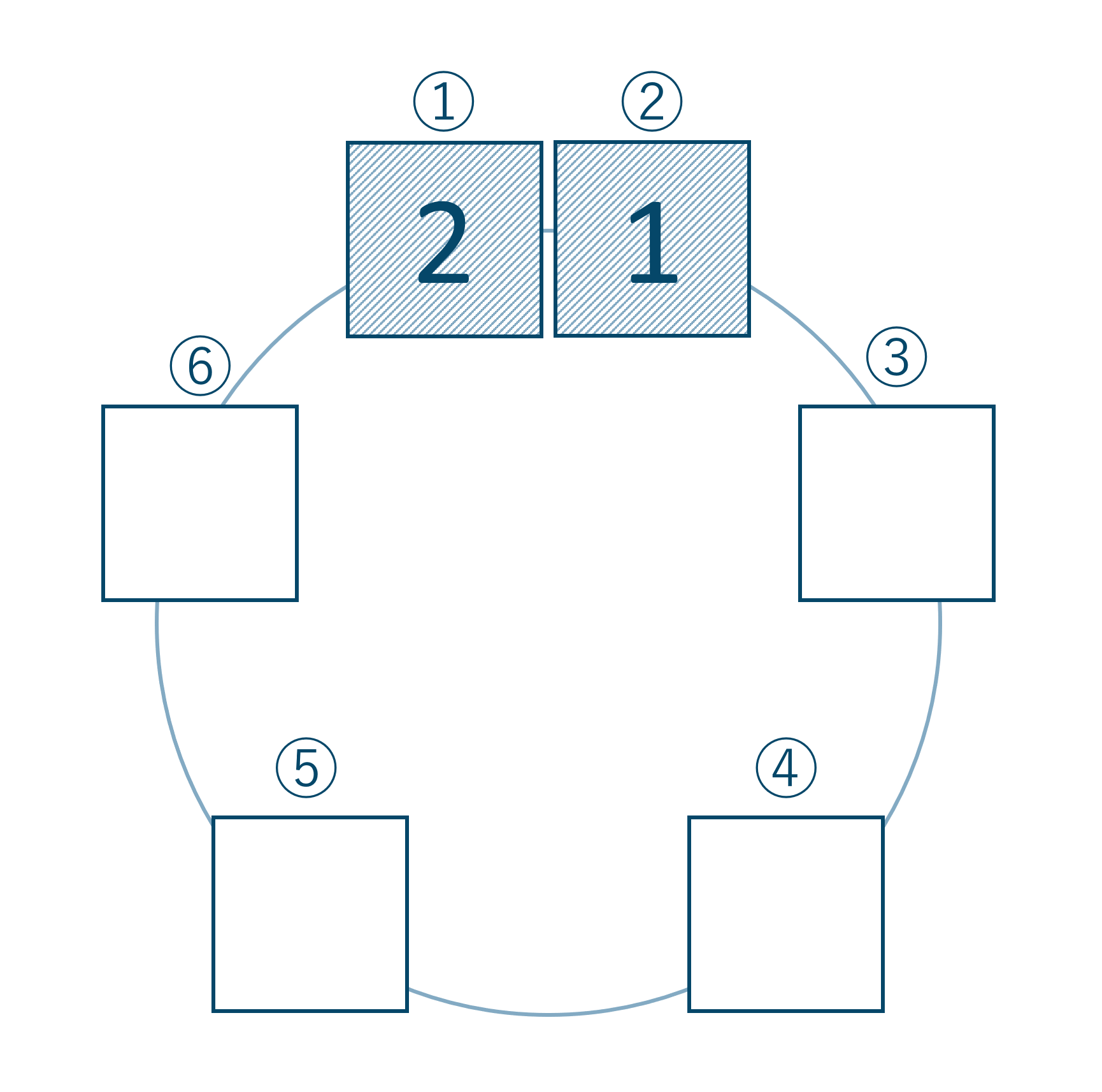
先生2人は必ず隣り合わないといけません。この隣り合う先生2人の場所を①と②にし固定ます。
2席を使って固定し、その固定された中での場合の数を考えると$$~~~2\times 1=2$$よって2通りとなります。
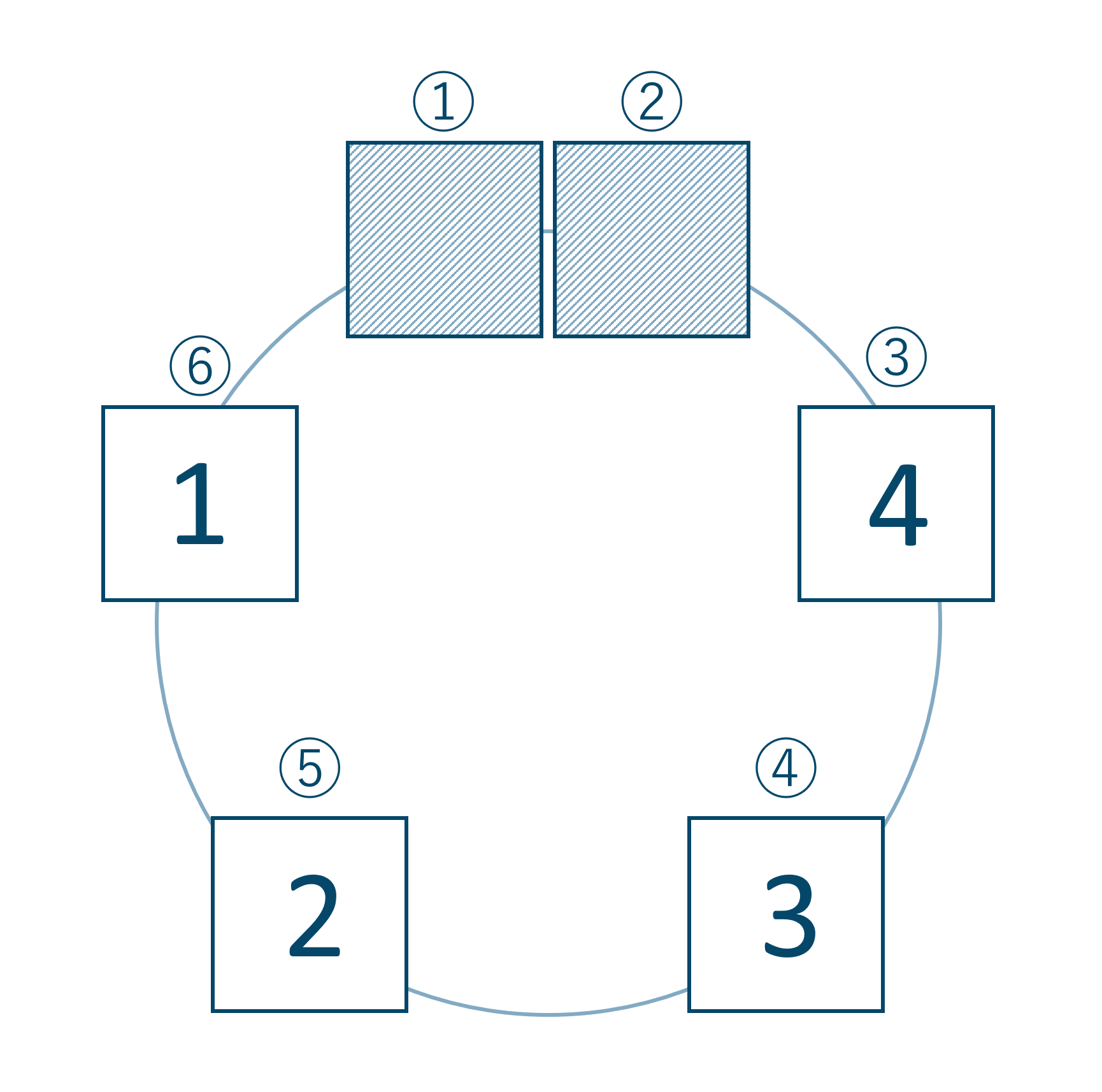
次にこの先生2人以外の4人を座らせます。先生2人が固定されているので、円順列の回転によるダブりは考えなくて良くなっています。③~⑥の席の順列を考えると、
よって4人の順列となるので計算式は、$$~~~4!=4\times 3\times 2\times 1=24$$よって24通りとなります。
以上よりこの2つの場合の数は「連続して起こる」ので積の法則より$$~~~2\times 24=48$$よって、答えは48通りとなる。
問題解説(3)
\({\small (3)}~\)先生2人が向い合う座り方
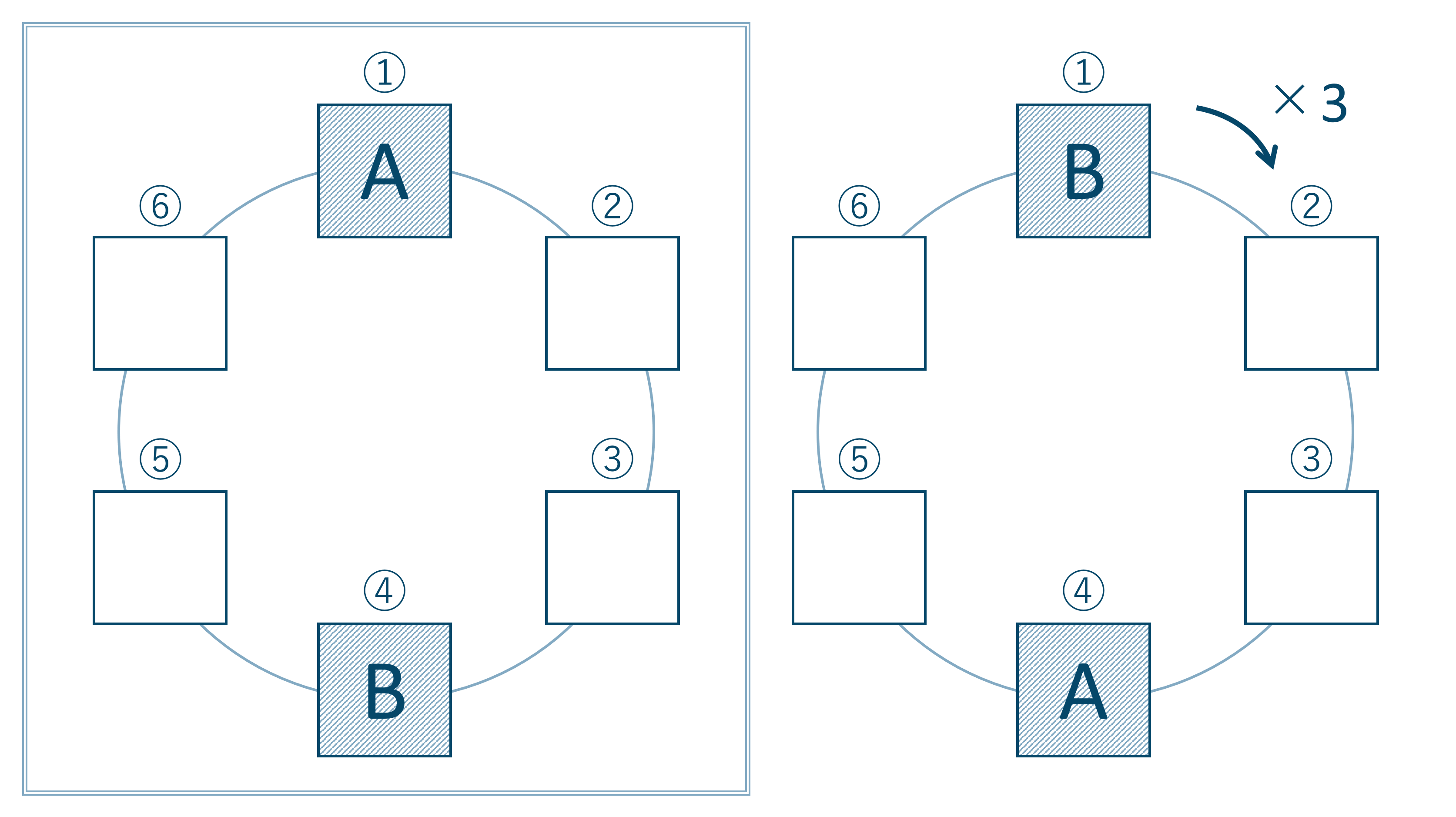
向い合う先生2人をAとBとしたとき、AとBを入れ替えて回転させると入れ替える前と同じになります。
図の2つの場合は回転させたとき同じになるので、先生2人を向い合せに座らせる場合はその入れ替わりは考えなくてよくなり、その場合の数は1通りとなります。
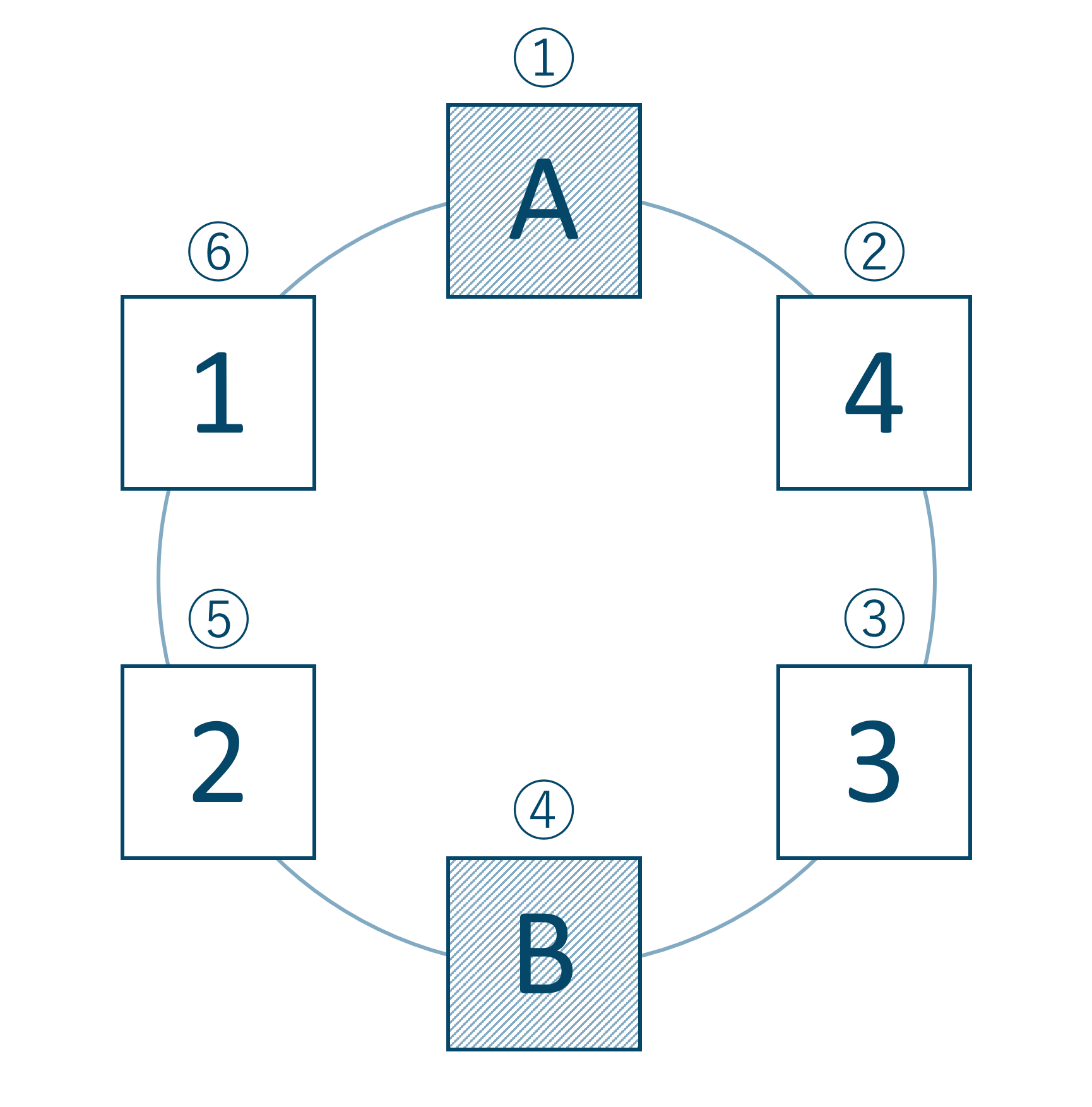
次に残りの4人を座らせます。このとき、先生2人が固定されて座っているので、残りの4席に座っていく順列として考えるので、
よって、計算式は$$~~~4!=4\times 3\times 2\times 1=24$$よって、24通りとなります。
したがって、この2つの場合の数は「連続して起こる」ので積の法則より、$$~~~1\times 24=24$$よって、答えは24通りとなる。
今回のまとめ
条件があっても基本は円順列に変わりないので「固定させる」を考えましょう!また、「隣り合うとき」と「向い合うとき」の解法もしっかりと覚えておきましょう。