重複を許す順列
Point:タイトル異なる \(n\) 個のものから重複を許し \(r\) 個並べる順列は、
\(r\) 個の箱を描いて、それぞれの箱に入る選択肢はすべて \(n\) 通りあるので
\(r\) 個の箱を描いて、それぞれの箱に入る選択肢はすべて \(n\) 通りあるので
$$n \times n \times n \times \cdots \times n=n^r$$
となります。
問題解説:重複を許す順列
問題解説(1)
問題次の場合の数を答えよ。
\({\small (1)}~\)\( a,b,c,d,e\) の5つの文字から、重複を許して3つの文字を一列に並べる並べ方
\({\small (1)}~\)\( a,b,c,d,e\) の5つの文字から、重複を許して3つの文字を一列に並べる並べ方
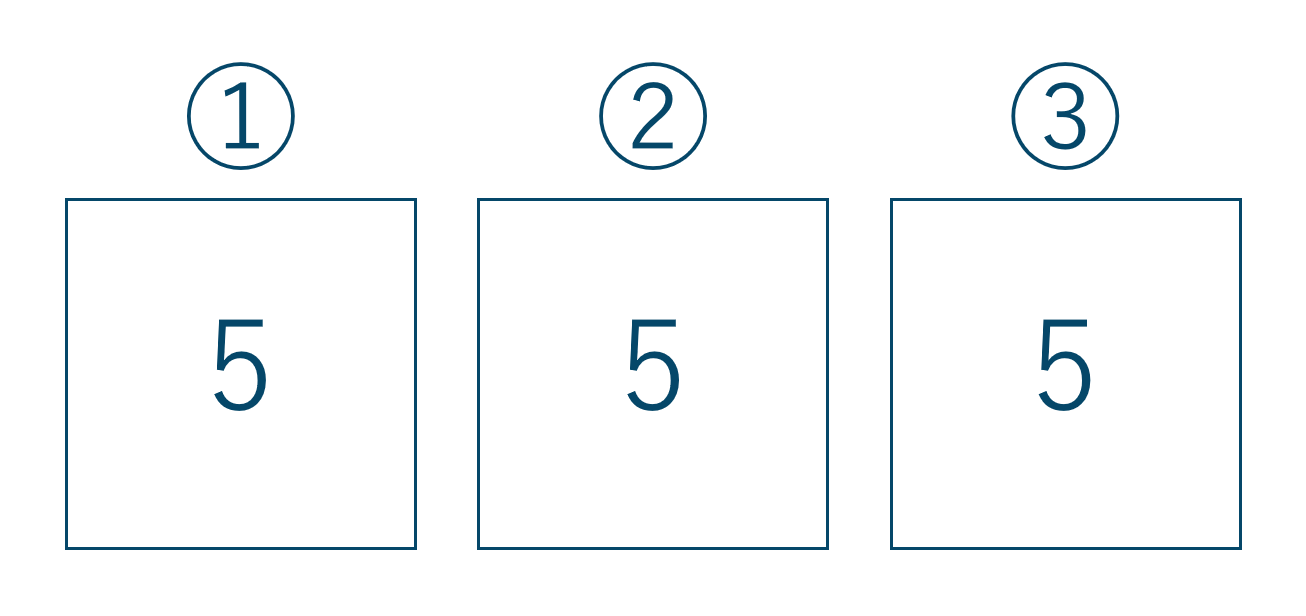
箱を3つ描いて考えると、
このときそれぞれの箱に入る文字の場合の数は①で5通り、②でも③でもすべての文字が使えるのでそれぞれ5通りとなります。
よって、積の法則より$$~~~5\times 5\times 5=125$$答えは125通りとなります。
重複順列の公式を使うと計算式は、$$~~~5^3=125$$よって、答えは125通りとなります。
問題解説(2)
問題次の場合の数を答えよ。
\({\small (2)}~\)0 , 1 , 2 , 3 , 4 の5つの数字から、重複を許して3桁の自然数を作る作り方
\({\small (2)}~\)0 , 1 , 2 , 3 , 4 の5つの数字から、重複を許して3桁の自然数を作る作り方
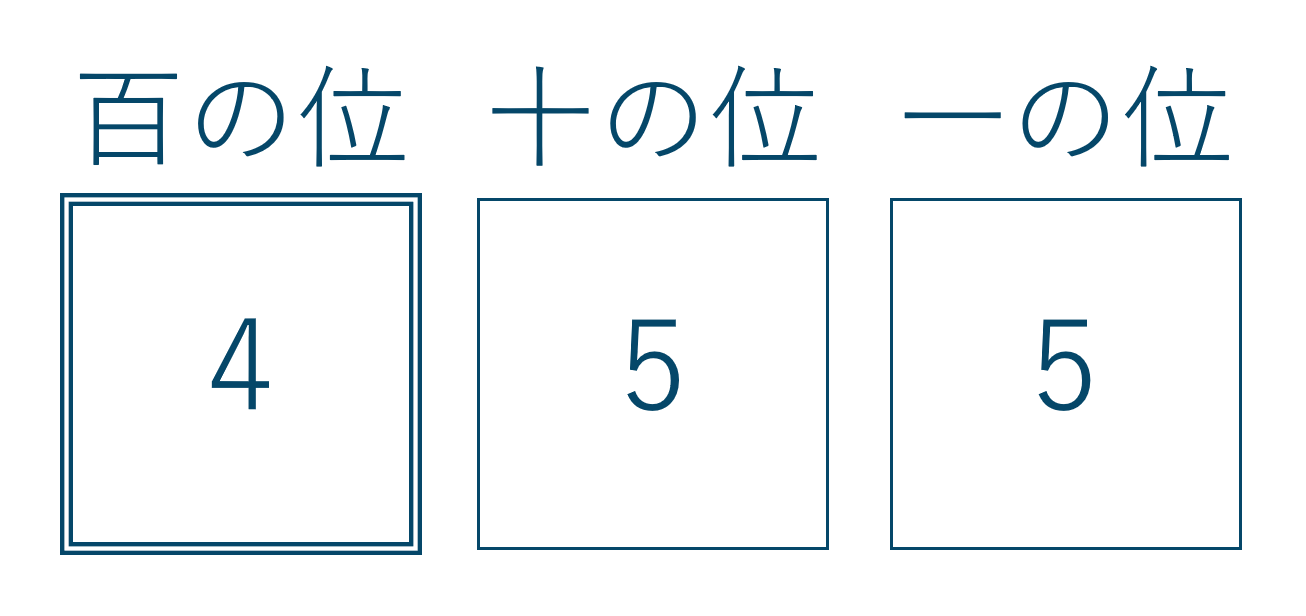
3桁の整数を作るので百の位、十の位、一の位の箱を描きます。それで百の位から順に数字の入れる場合の数を書いていきましょう。百の位にはを0除く4つの数字が入るので4通り。十の位と一の位には0を含むすべての数字が入れるのでそれぞれ5通りとなります。
したがって、積の法則より$$~~~4 \times 5 \times 5=100$$答えは100通りとなります。
今回のまとめ
(1)の問題では公式が使えるパターンですが、(2)は公式がそのまま使えません。重複順列でも順列の基本解法である「箱を描いて、順番に場合の数を書く」を用いて解きましょう。

【問題一覧】数学A:場合の数と確率
このページは「高校数学A:場合の数と確率」の問題一覧ページとなります。解説の見たい単元名がわからない...