3つのグループに分ける方法
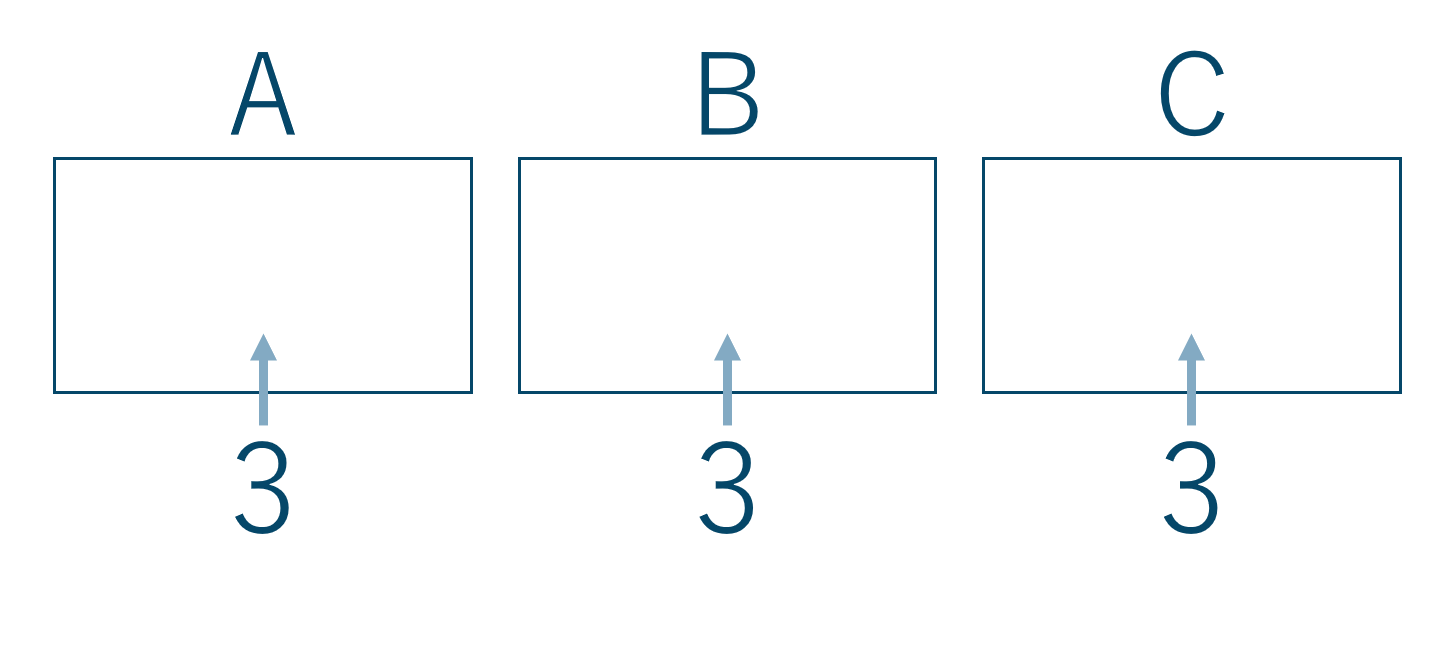
「3つの部屋A、B、Cに分ける」ときや「人数にバラバラで区別できる」ときは3つの箱を描きそれぞれの箱に入れる組合せを考えて、積の法則より場合の数を求めましょう。
・グループに区別がない
「すべてのグループに同じ人数が入る」ときは、グループに区別がありません。
このときは、
① グループに区別があると考えて場合の数を計算します。
② この場合の数を(グループの数)!で割ります。
※区別がないグループの数の階乗で割ると覚えておきましょう。
問題解説:3つのグループに分ける
問題解説(1)
\({\small (1)}~\)3人ずつA、B、Cの3部屋に分ける
この問題ではA、B、Cの3部屋とあるのでグループに区別があります。ですので、A、B、Cの3つの箱を考えて1部屋ずつ場合の数を考えていきましょう。

Aの部屋には9人の中から3人を選んで入るので計算式は \( {}_{9}{\rm C}_{3} \) となる
Bの部屋にはAに入った3人以外の6人から3人を選んで入るので計算式は \( {}_{6}{\rm C}_{3} \) となる
Cの部屋には残りの3人から3人を選んで入るので計算式は \( {}_{3}{\rm C}_{3} \) となる
これらは「連続して起こる」ので積の法則より$$~~~~~{}_{9}{\rm C}_{3} \times {}_{6}{\rm C}_{3} \times {}_{3}{\rm C}_{3}$$$$~ =\frac{9 \times 8 \times 7}{3 \times 2 \times 1} \times \frac{6 \times 5 \times 4}{3 \times 2 \times 1} \times 1=1680$$よって、答えは1680通りとなります。
問題解説(2)
\({\small (2)}~\)3人ずつ3組に分ける
次の問題では3人ずつ3組に分けるだけですのでグループに区別がありません。
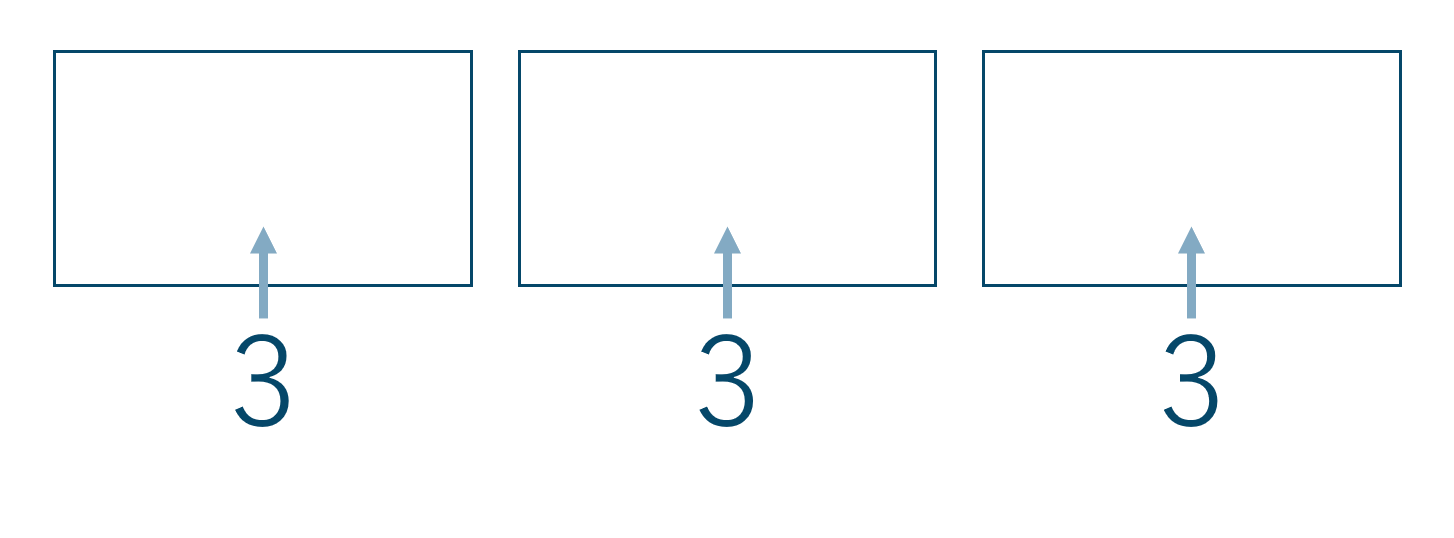
ですのでまずはグループに区別があると考えて計算をし、その後で(グループの数)!で割る必要があります。
グループに区別があるときは、(1)と同じになるので1680通りとなります。また、3つの区別ができないグループに分けるので \( 3! \) で割ると計算式は、$$~~~1680 \div 3! = \frac{1680}{3\times 2\times 1}=280$$よって、答えは280通りとなります。
問題解説(3)
\({\small (3)}~\)4人、3人、2人に分ける
この問題は分けるだけで区別はついていません、しかし、4人、3人、2人に分けると人数に違いが出ているので区別がついていると同じ事となります。
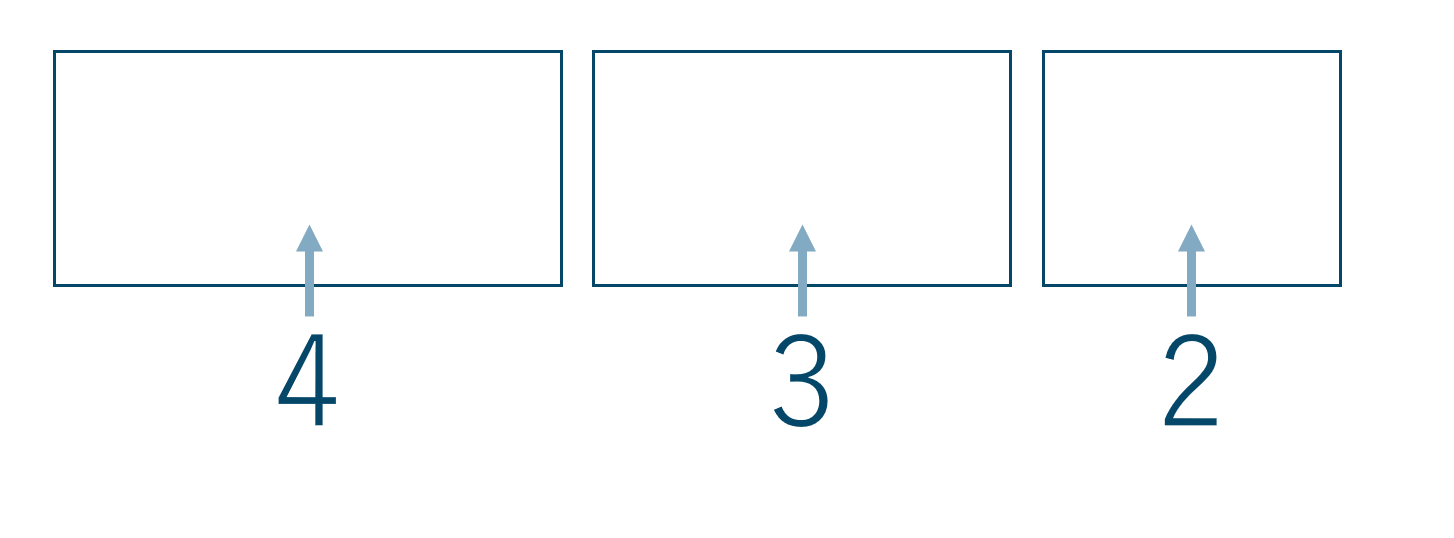
よって、9人から4人を選ぶ組合せは \( {}_{9}{\rm C}_{4} \) となる
次に、残りの5人から3人を選ぶ組合せは \( {}_{5}{\rm C}_{3} \) となる
次に、残りの2人から2人を選ぶ組合せは \( {}_{2}{\rm C}_{2} \) となる
これらは「連続して起こる」ので積の法則より$$~~~~~{}_{9}{\rm C}_{4} \times {}_{5}{\rm C}_{3} \times {}_{2}{\rm C}_{2} $$$$~=\frac{9 \times 8 \times 7 \times 6}{4 \times 3 \times 2 \times 1} \times \frac{5 \times 4 \times 3}{3 \times 2 \times 1} \times 1=1260$$よって、答えは1260通りとなります。
今回のまとめ
3つのグループに分ける問題を見ていきました。グループに区別があるかどうかの判断をして解法を選択できるようになりましょう。また、グループに区別がないときでも、人数に差がある場合は区別があると考えましょう。




