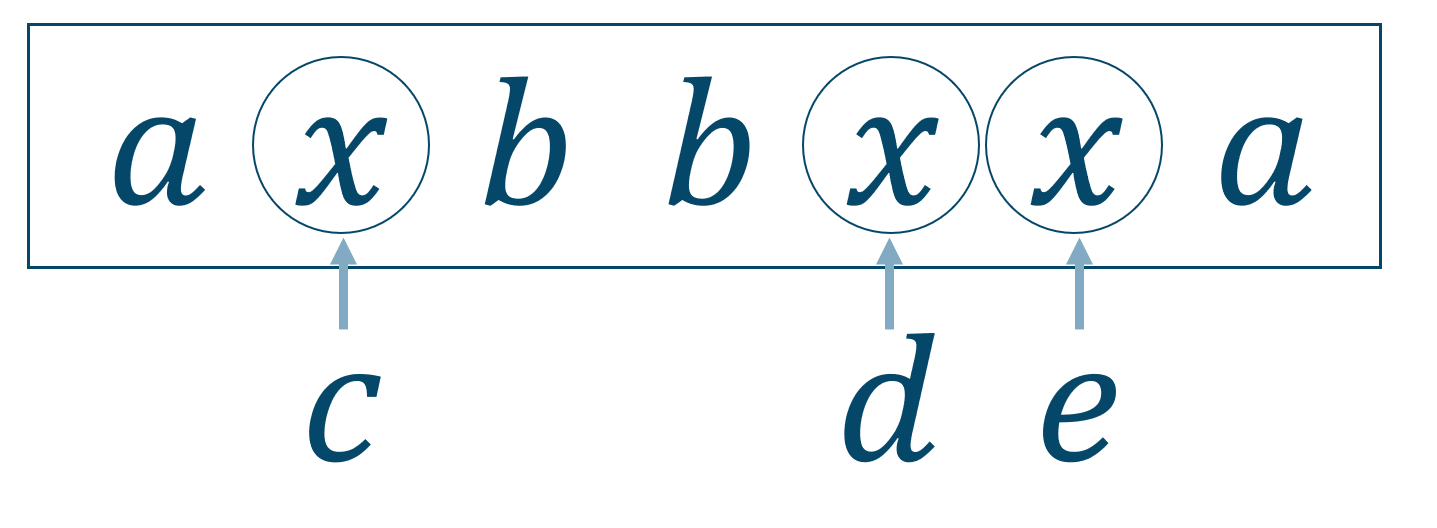同じものを含む順列の解法
例題:\( a,b,b,b\) の4つの文字を一列に並べる
同じものを含む順列では、まずは同じものでも一度区別して考えましょう。ですので\( b,b,b\) を \( b_1,b_2,b_3\) と区別します。\( a\) と合わせて4つの文字を一列に並べるので$$~~~4!=4 \times 3 \times 2 \times 1=24$$よって24通りとなります。
このままでは \( b \) を区別したままなので、その区別をなくしたときに出るダブりを消しましょう。
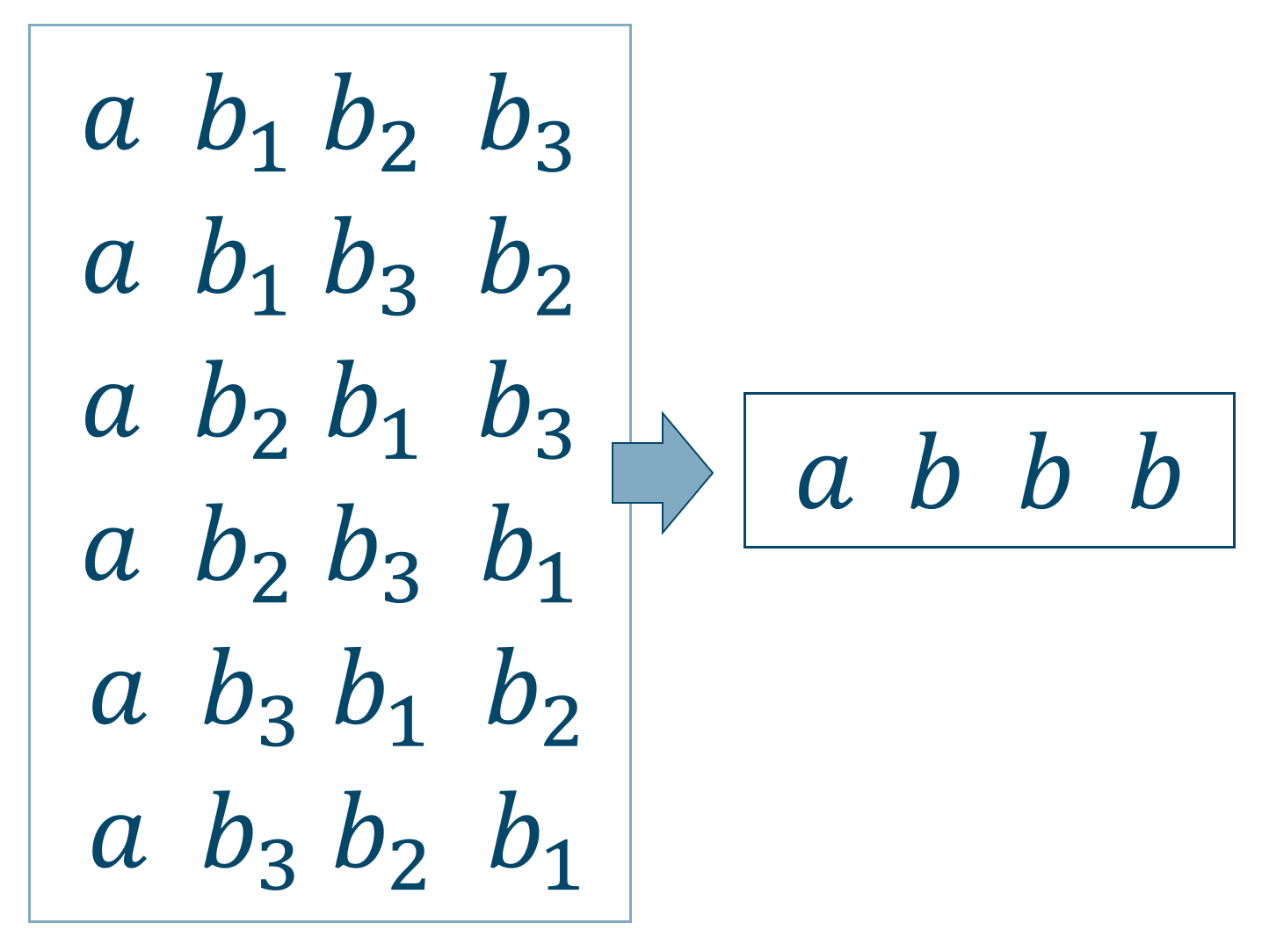
計算式は、(区別ができないものの数)! で割るので、$$~~~\frac{24}{3!}=\frac{24}{3\times2\times1}=\frac{24}{6}=4$$よって、答えは4通りとなります。
例題:\( a,b,c,d\) の4つの文字を一列に並べるとき、\(b,c,d\) がこの順になる場合の数
文字を並べ終わったとき、左から順に\( b,c,d\) だけを見ていくと、\(b\)→\(c\)→\(d\)の順になっていればよいことになります。
この問題の解法の手順は、
① 順に並べる \(b,c,d\) をすべて同じ文字 \(x\) に置き換えます。
② 同じ文字を含む順列として計算します。
よって、\( a,x,x,x\) の同じものを含む順列となるので、$$~~~\frac{4!}{3!}=\frac{4\times 3\times 2\times 1}{3\times 2\times 1}=4$$よって、答えは4通りとなります。
問題解説:同じものを含む順列
問題解説(1)
\({\small (1)}~\)\( a,a,b,b,b,c,d \) の7つの文字を一列に並べる
同じもので区別ができないものが \( a \) が2個、\( b \) が3個あります。全体で7個の文字があるので計算式は、$$~~~~~\frac{7!}{2!\cdot 3!}$$$$~=\frac{7\times6\times5\times4\times3\times2\times1}{2\times1\times3\times2\times1}$$$$~=420$$よって、答えは420通りとなります。
問題解説(2)
\({\small (2)}~\)\( a,a,b,b,c,d,e\) の7つの文字を一列に並べるとき、\( c,d,e\) がこの順になる
「\( c,d,e\) がこの順になる」とは例えば7つの文字を一列並べたとき
となったとき、左から順に\( c,d,e\) だけを見ていくと、\(c\)→\(d\)→\(e\)の順になっています。このとき他の文字はどこの位置にあるかは関係ありません。
この3つの文字\( c,d,e\) をすべて \( x\) と置き換えます。\( a,a,b,b,x,x,x\) を一列に並べる順列となるので、例えば次のように並べたとき、
\( x\) の部分には実際には \( c,d,e\) が入ります。その入れ方は左から順に \( c,d,e\) と1通りだけ入るます。
よって\( x\) に変えて計算すれば、左から順に \( c,d,e\) と入れたときの計算と同じになります。
\( a,a,b,b,x,x,x\) の7個の文字を並べるとき、\( a \) が2個、\( b \) が2個、\( x \) が3個あるので同じものを含む順列より、$$~~~~~\frac{7!}{2!\cdot 2! \cdot 3!}$$$$~=\frac{7\times6\times5\times4\times3\times2\times1}{2\times1\times2\times1\times3\times2\times1}$$$$~=210$$よって、答えは210通りとなります。
今回のまとめ
同じものを含む順列は解法をパターンとして覚えておきましょう。基本は(区別できないものの数)!で割るです!また、「左から順に並べる」パターンも解法を覚えてできるようになりましょう。