最短経路問題の解法
例えば次の図においてAからBまでの最短経路の場合の数は、
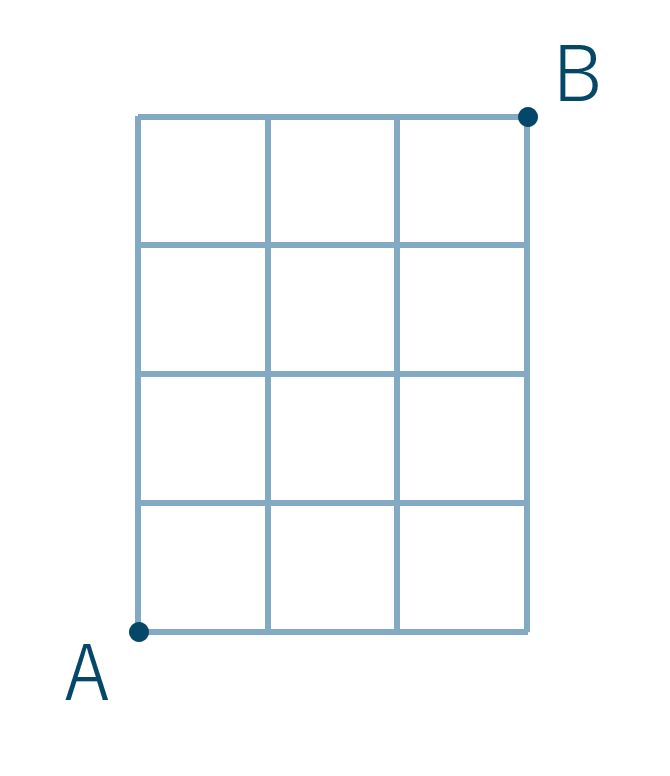
最短で進むので、区画分けより右に3回、上に4回進めば最短で目的地まで行けます。よって次の7つの記号を並べ替えたらその分だけ新しい経路ができます。
「 → → → ↑ ↑ ↑ ↑ 」なら
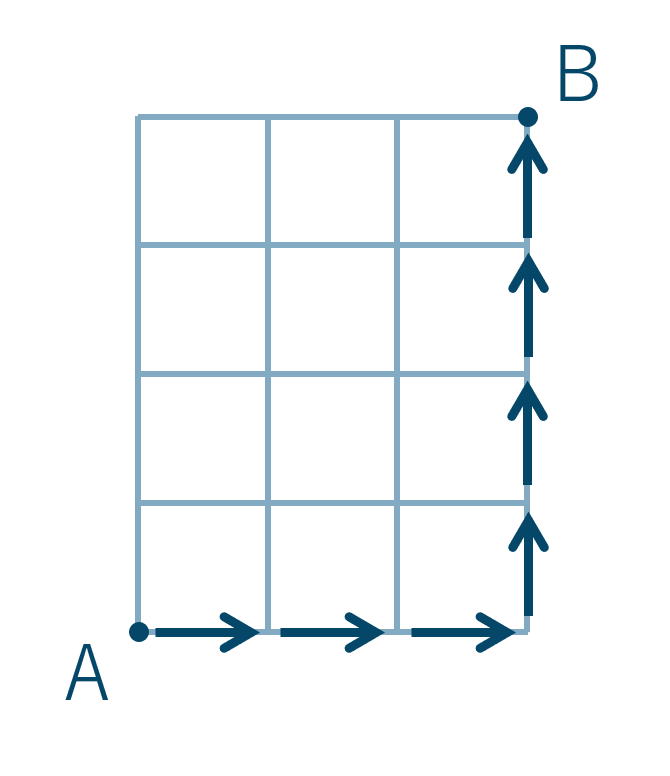
「 → ↑ → → ↑ ↑ ↑ 」なら
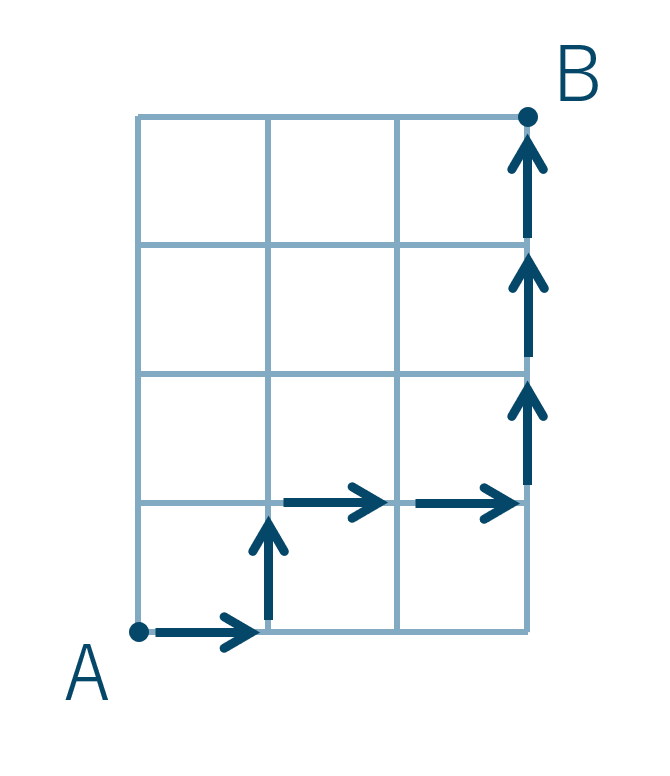
したがって→が3つ、↑が4つの合計7つの記号の同じものを含む順列として計算できるので、$$~~~~~\frac{7!}{3!\cdot 4!}$$$$~=\frac{7\times6\times5\times4\times3\times2\times1}{3\times2\times1\times4\times3\times 2\times1}$$$$~=35$$よって、答えは35通りとなります。
このように最短経路問題は2方向の矢印の同じものを含む順列として計算できます。
問題解説:最短経路問題
問題解説(1)
\({\small (1)}~\)AからBまでの最短経路
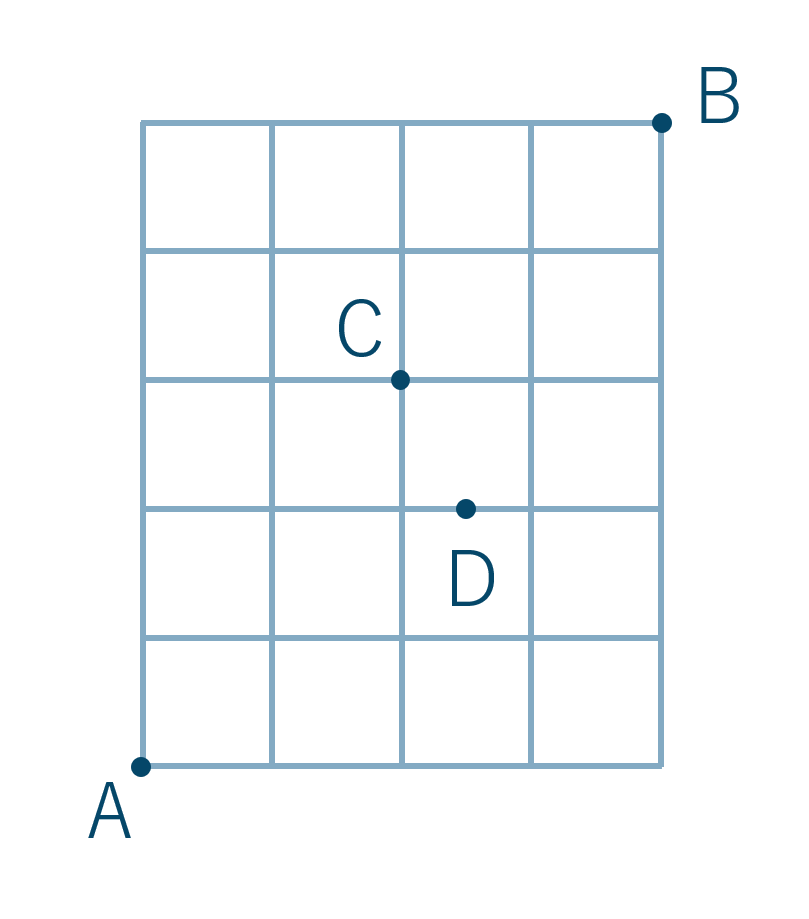
AからBに行くには、→に4回と↑に5回の合計9回進むことになります。同じものを含む順列で考えると、$$~~~~~~\frac{9!}{4!\times 5!}$$$$~=\frac{9\times8\times7\times6\times5\times4\times3\times2\times1}{4\times3\times2\times1\times5\times4\times3\times2\times1}$$$$~=126$$よって、答えは126通りとなります。
問題解説(2)
\({\small (2)}~\)AからBまでの最短経路でCを必ず通る経路




次の問題では、Aから一度Cに行きBまで行きます。ですので「AからCまでの経路」と「CからBまでの経路」に分けて考えましょう。
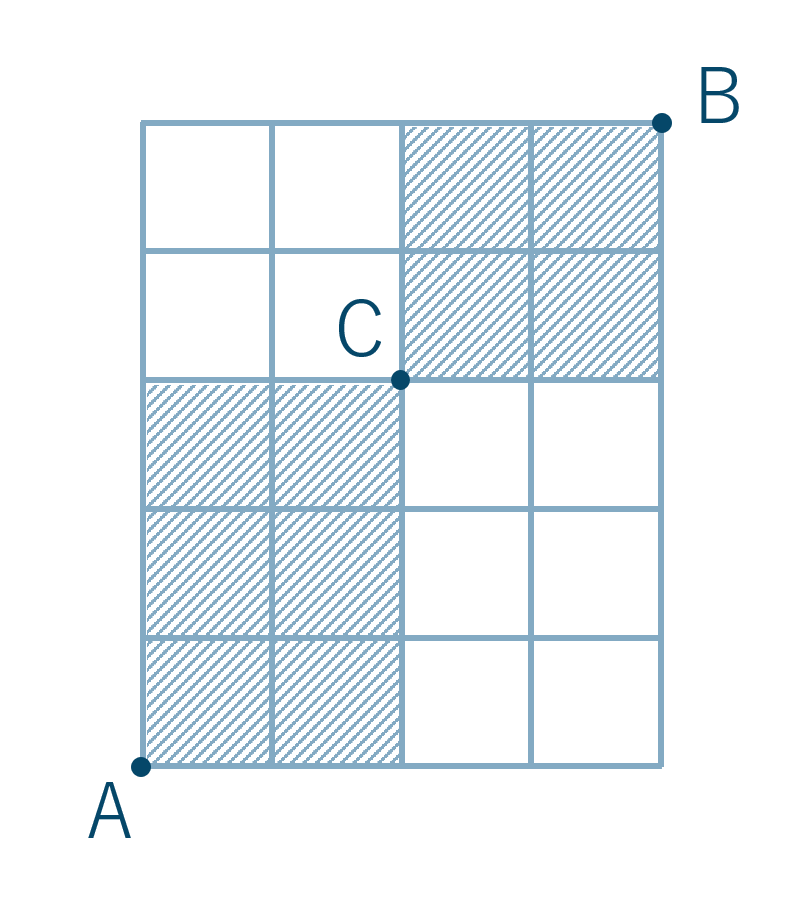
まずはAからCまでの経路は、→に2回、↑に3回の合計5回進むので、同じものを含む順列より$$~~~\frac{5!}{2!\times 3!}=\frac{5\times4\times3\times2\times1}{2\times1\times3\times2\times1}=10$$よって、10通りとなります。
次にCからBまでの経路は、→に2回、↑に2回の合計4回進むので、同じものを含む順列より$$~~~\frac{4!}{2!\times 2!}=\frac{4\times3\times2\times1}{2\times1\times2\times1}=6$$よって、6通りとなります。
これらはAからC、CからBと「連続して起こる」ので積の法則より$$~~~10 \times 6 =60$$したがって、答えは60通りとなります。
問題解説(3)
\({\small (3)}~\)AからBまでの最短経路でDを通らない経路




この問題ではDを通らずにBまで行かないといけませんが、それを考えるのは難しいのでDを必ず通る場合の数を考えましょう。
「AからBに行くすべての場合の数」から「Dを必ず通る場合の数」を引けば「AからDを通らずにBに行く場合の数」を求めることができます。
Dを必ず通る場合の数は、
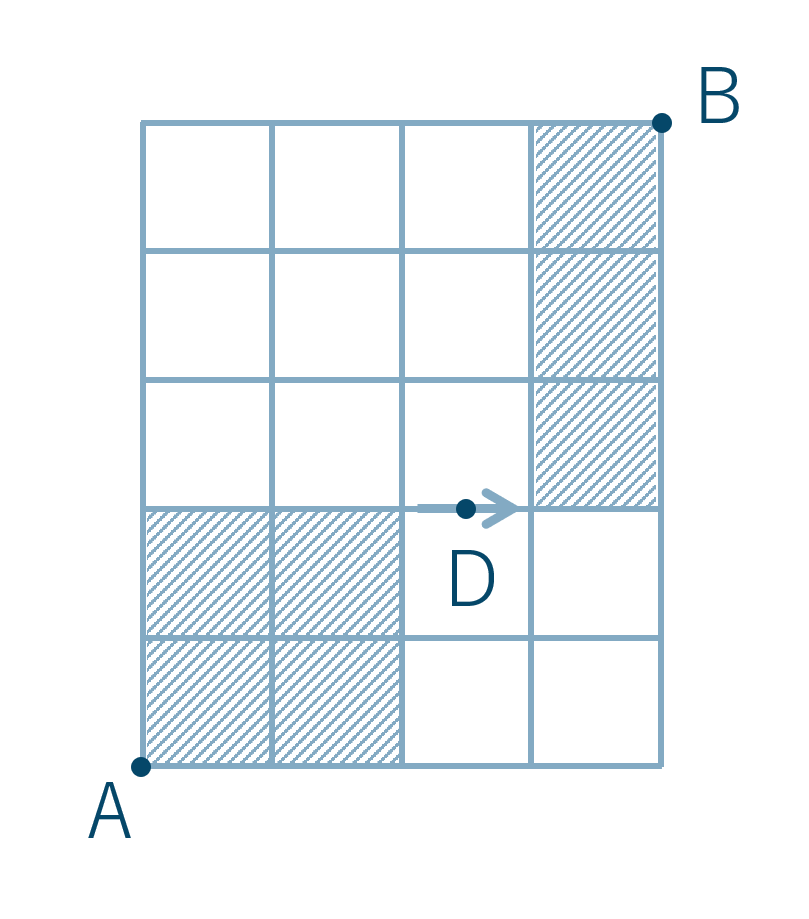
① AからDの左の十字路まで
② Dの道
③ Dの右の十字路からBまで
と進めばよいことになります。
AからDの左の十字路に行くには、→に2回、↑に2回の合計4回進めばよいので、同じものを含む順列より$$~~~\frac{4!}{2!\times 2!}=\frac{4\times3\times2\times1}{2\times1\times2\times1}=6$$よって、6通りとなります。
次にDの道を進むのは1通りとなります。
次にDの右の十字路からBまで行くには、→に1回、↑に3回の合計4回進めばよいので、同じものを含む順列より$$~~~\frac{4!}{3!}=\frac{4\times3\times2\times1}{3\times2\times1}=4$$よって、4通りとなります。
したがって、これらは「連続して起こる」ので積の法則より$$~~~6 \times 1 \times 4 =24$$よって、24通りとなります。
また、AからBに行くすべての場合の数は(1)より126通りとなります。
したがって、$$~~~126 – 24 =102$$答えは102通りとなります。
今回のまとめ
最短経路問題は「→」と「↑」の矢印の同じものを含む順列として計算できます。また条件があるパターンの解法も合わせて覚えておきましょう!




