さいころの確率

問題解説：さいころの確率

問題解説(1)

まずは２つのさいころをAとBに区別して表を作ると次のようになります。

表より、すべての起こりうるの場合の数は36通りとなります。
 
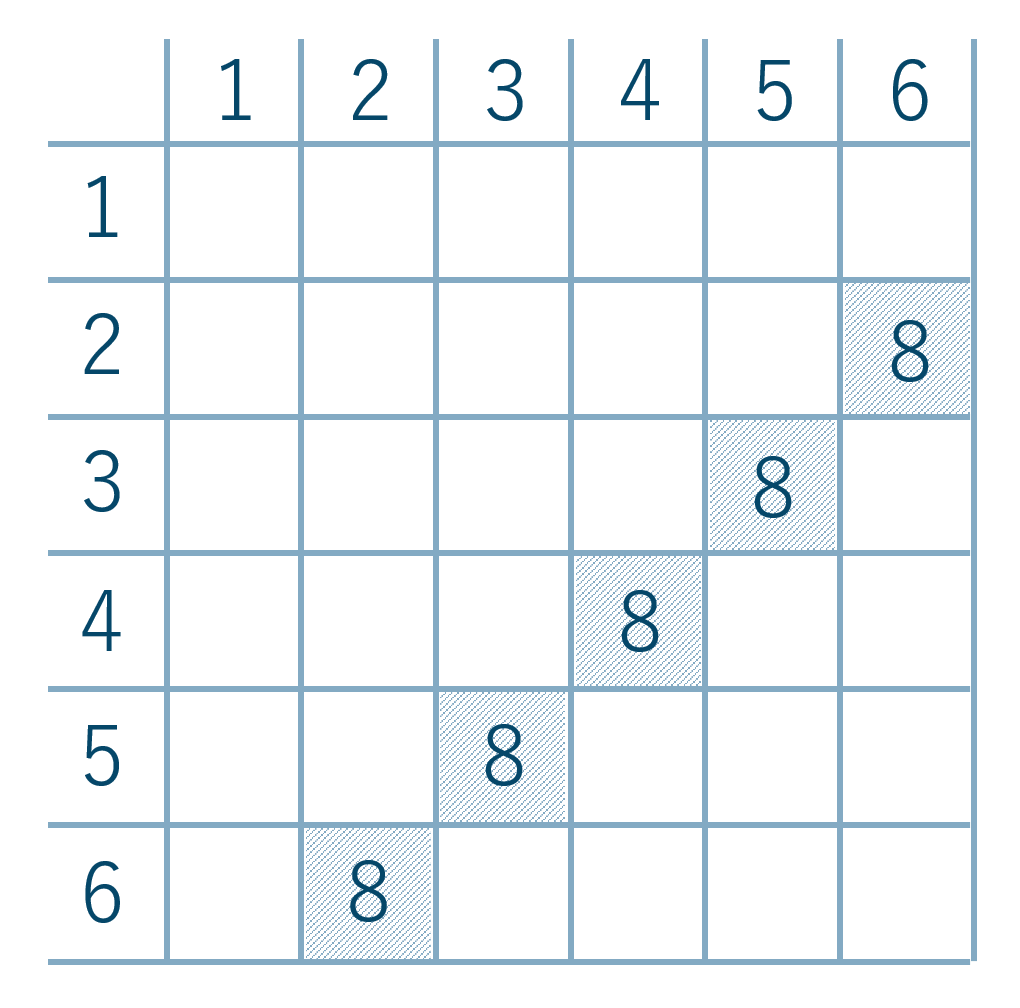
また、目の和が8となるのは、

表より、条件の場合の数は5通りとなります。
 
よって、答えは \( {\Large \frac{5}{36}} \) となります。

問題解説(2)

問題(1)と同様に２つのさいころを区別して表を作ると、
すべての起こりうる場合の数は36通りとなります。
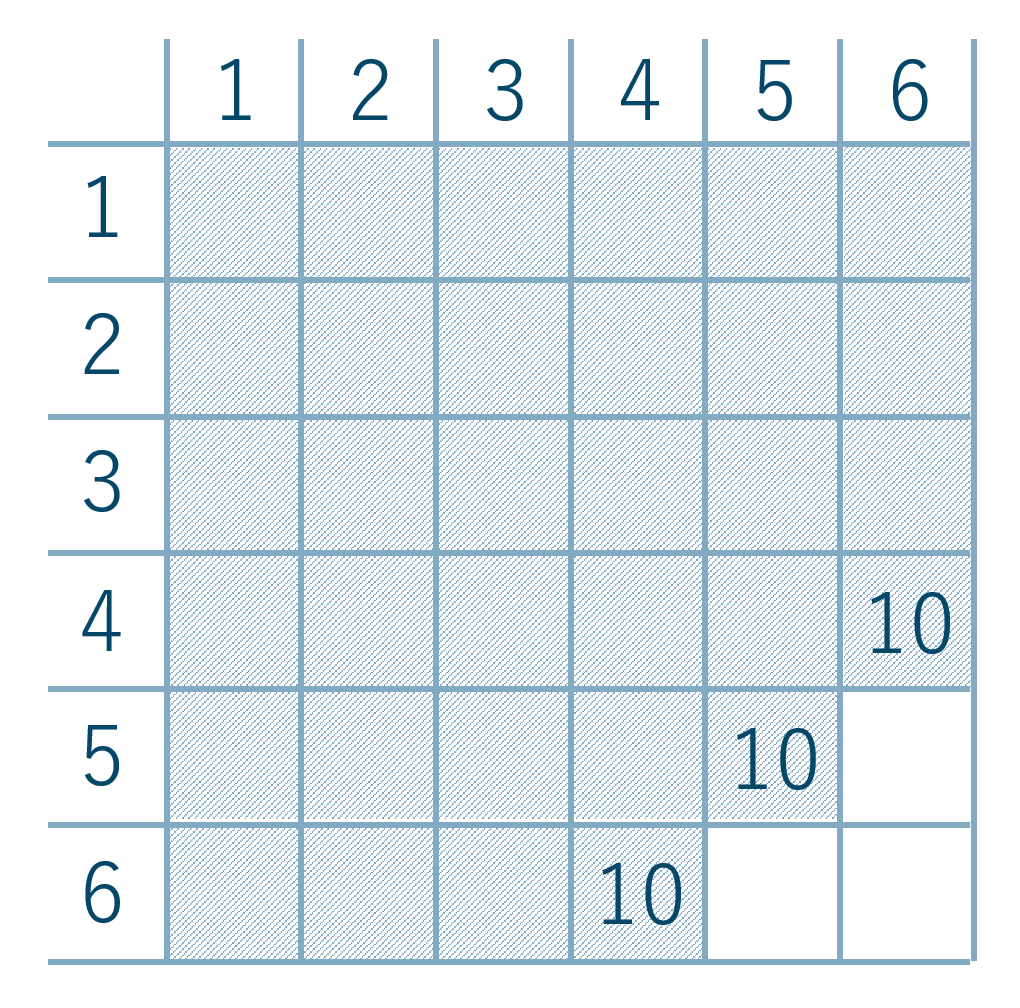
次に、目の和が10以下となるのは、

この表より33通りとなります。
 
したがって求める確率は、$$~~~\frac{33}{36}=\frac{11}{12}$$よって、答えは \( {\Large \frac{11}{12}} \) 通りとなります。
 
【別解】
問題(2)では余事象の確率を用いて少し簡単に解くことができます。
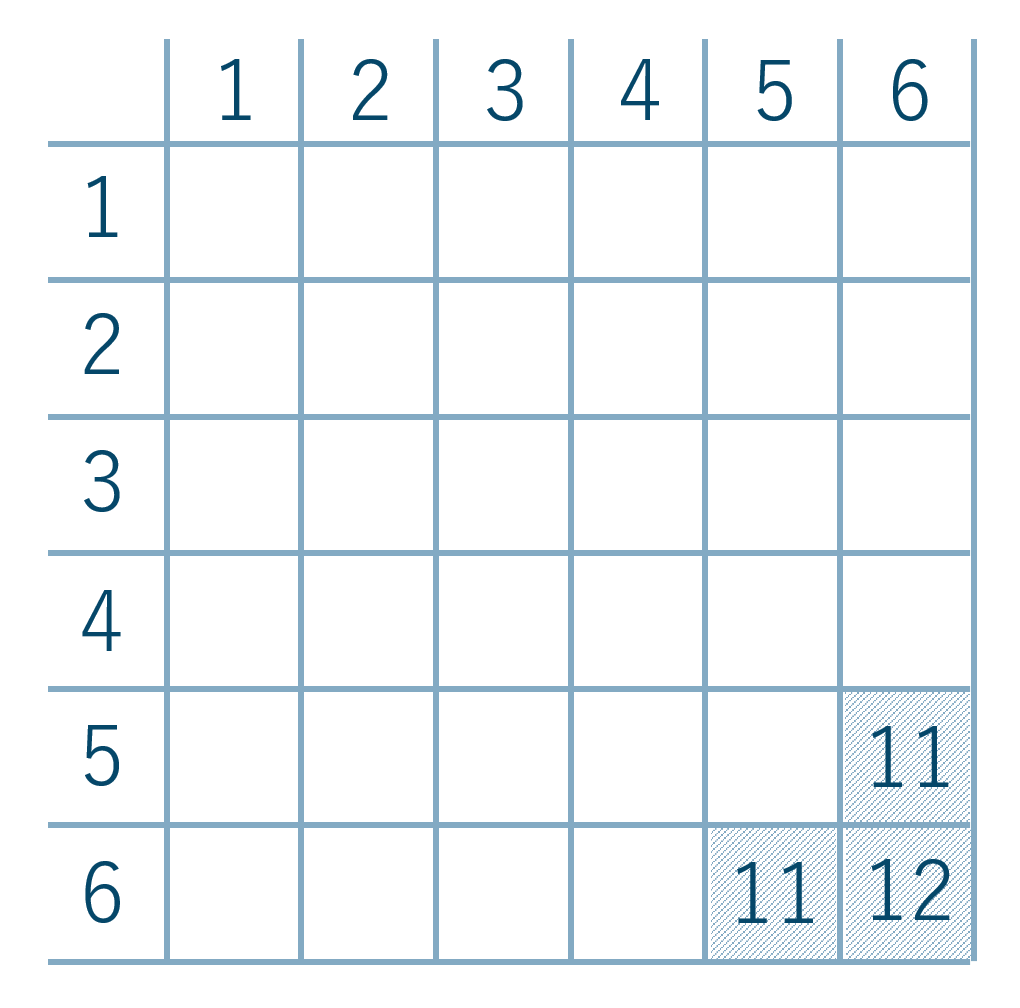
「目の和が10以下」の否定は「目の和が11以上」より表を作成すると、

「目の和が11以上」となるのは3通りなので確率は、$$~~~\frac{3}{36}=\frac{1}{12}$$となります。
したがって余事象の確率の考え方より「目の和が10以下」のなる確率は、$$~~~1-\frac{1}{12}=\frac{11}{12}$$よって、答えは \( {\Large \frac{11}{12}} \) となります。

今回のまとめ

さいころ２個の確率はとにかく表を描いて数えて求めましょう！視覚的に解くことが大切になります。また、余事象の確率は計算が楽になることが多いのでできるようになりましょう！

【問題一覧】数学Ａ：場合の数と確率

このページは「高校数学Ａ：場合の数と確率」の問題一覧ページとなります。解説の見たい単元名がわからない...

yorikuwa.com