コインを投げる反復試行の確率
例えばコインを投げる試行を3回繰り返すとき、そのうち2回が表である確率を求めると
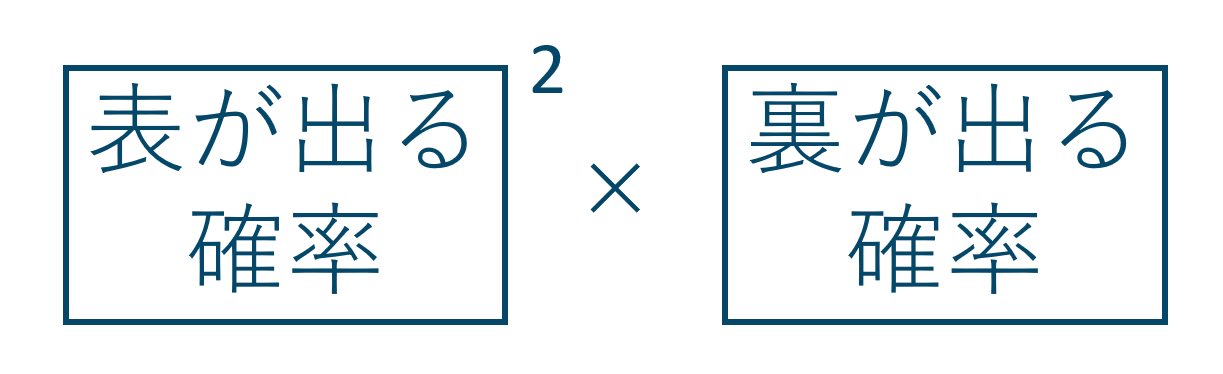
だけでいいように思えますが、これだけでは何番目に表が出るかを考えていません。
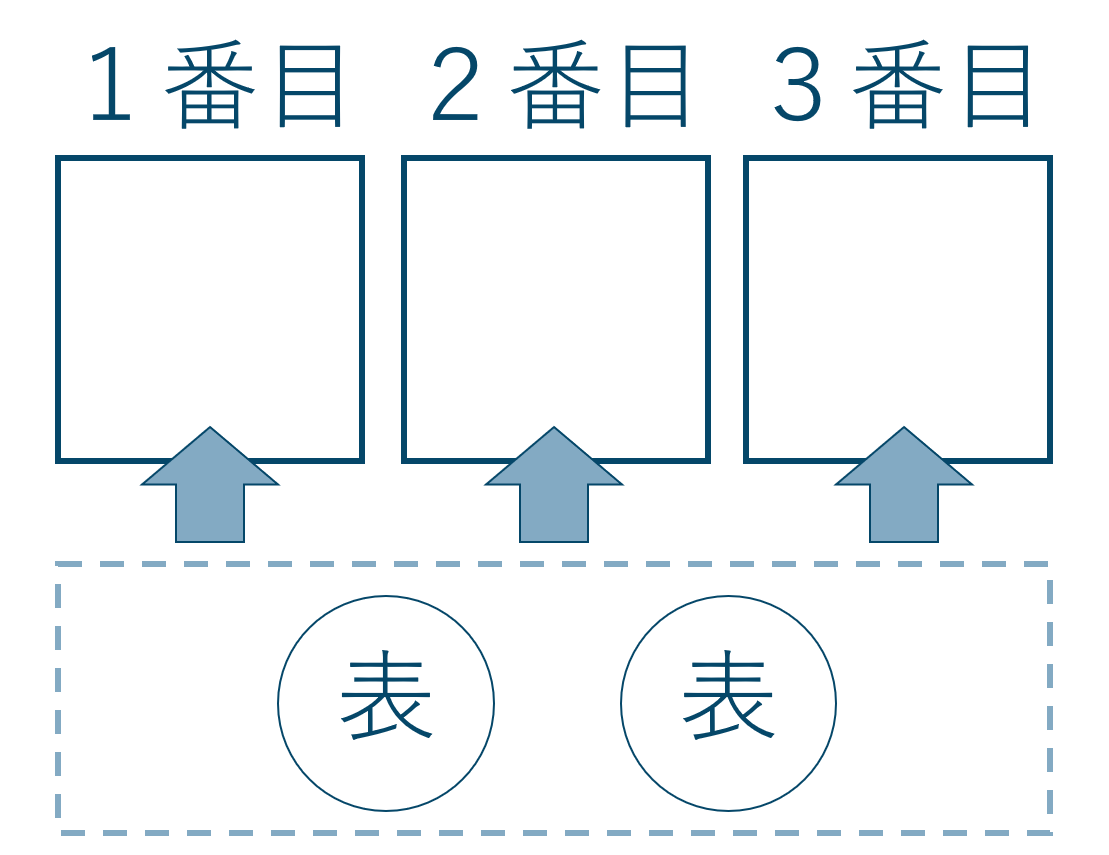
図にあるように3回中2回が何回目に表がくるかの場合の数である3か所から表が出る2か所を選ぶ組合せ \( {}_{3} {\rm C}_{2} \) 通りをかける必要があります。
よって、求める確率は

となり計算式は、$$~~~~~~{}_{3} {\rm C}_{2}\times \left(\frac{1}{2}\right)^2 \times \frac{1}{2}$$$$~=\frac{3\times2}{2\times1}\times \frac{1}{4} \times \frac{1}{2} $$$$~=\frac{3}{8}$$答えは \( {\Large \frac{3}{8}} \) となります。
\( {}_{3} {\rm C}_{2} \) は1回目、2回目、3回目の3か所から表が出る2か所を選ぶ組合せとなっていて、残った1か所はそのまま裏が出る所となります。よって、裏が何回目に出るかは考えなくてもよいことになります。
問題解説:反復試行の確率①(コイン)
問題解説(1)
\({\small (1)}~\)表がちょうど4回出る
コインを投げて表が出る確率は \( {\Large \frac{1}{2}} \) で裏が出る確率も \( {\Large \frac{1}{2}} \) となります。
ここで、5回中4回表が出るので求める確率は、
となるので計算式は$$~~~~~~{}_{5} {\rm C}_{4}\times \left(\frac{1}{2}\right)^4 \times \frac{1}{2}$$$$~=\frac{5\times4\times3\times2}{4\times3\times2\times1}\times \frac{1}{16} \times \frac{1}{2}$$$$~ =5\times \frac{1}{32}$$$$~=\frac{5}{32}$$答えは \( {\Large \frac{5}{32}} \) となります。
問題解説(2)
\({\small (2)}~\)表がちょうど3回出る
コインを投げて表が出る確率は \( {\Large \frac{1}{2}} \) で裏が出る確率も \( {\Large \frac{1}{2}} \) となります。
ここで、5回中3回表が出るので求める確率は、
となるので計算式は$$~~~~~~{}_{5} {\rm C}_{3}\times \left(\frac{1}{2}\right)^3 \times \left(\frac{1}{2}\right)^2$$$$~=\frac{5\times4\times3}{3\times2\times1}\times \frac{1}{8} \times \frac{1}{4}$$$$~ =10\times \frac{1}{32}$$$$~=\frac{5}{16}$$答えは \( {\Large \frac{5}{16}} \) となります。
今回のまとめ
反復試行は様々な問題のパターンがあります。今回は一番基本となるパターンを解説しました。他のパターンにも応用できるように理解しできるようになりましょう!





