- 数学C|空間ベクトル「空間の3点が一直線上にある証明」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|空間の3点が一直線上にある証明
空間ベクトル 29平行六面体 \(\rm ABCD-EFGH \) と \( \triangle {\rm BDE} \) の重心 \(\rm O \) において、3点 \(\rm A~,~ O~,~ G \) は一直線上にあることを示す方法は?また、 \(\rm AO:OG \)の求め方は?
高校数学C|空間ベクトル
解法のPoint
空間の3点が一直線上にある証明
Point:空間の3点が一直線上にある証明
① 基本となる空間の3つのベクトルを文字でおく。
平行六面体 \(\rm ABCD-EFGH \) であれば、
\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\overrightarrow{\rm AD}=\overrightarrow{b}~,~\overrightarrow{\rm AE}=\overrightarrow{c} \)
② 一直線上を示す3点が \( \rm A~,~O~,~G \) であれば、\(\overrightarrow{\rm AG}\) と \(\overrightarrow{\rm AO}\) を①の位置ベクトルで表す。
③ \(\overrightarrow{\rm AG}=k\,\overrightarrow{\rm AO}\) となる実数 \(k\) があれば、3点 \( \rm A~,~O~,~G \) は一直線上にある。
空間の3点が一直線上にあることの証明の手順は、
① 基本となる空間の3つのベクトルを文字でおく。
平行六面体 \(\rm ABCD-EFGH \) であれば、
\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\overrightarrow{\rm AD}=\overrightarrow{b}~,~\overrightarrow{\rm AE}=\overrightarrow{c} \)
② 一直線上を示す3点が \( \rm A~,~O~,~G \) であれば、\(\overrightarrow{\rm AG}\) と \(\overrightarrow{\rm AO}\) を①の位置ベクトルで表す。
③ \(\overrightarrow{\rm AG}=k\,\overrightarrow{\rm AO}\) となる実数 \(k\) があれば、3点 \( \rm A~,~O~,~G \) は一直線上にある。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|空間の3点が一直線上にある証明
空間ベクトル 29
平行六面体 \(\rm ABCD-EFGH \) と \( \triangle {\rm BDE} \) の重心 \(\rm O \) において、3点 \(\rm A~,~ O~,~ G \) は一直線上にあることを示す方法は?また、 \(\rm AO:OG \)の求め方は?
高校数学C|空間ベクトル
[証明]
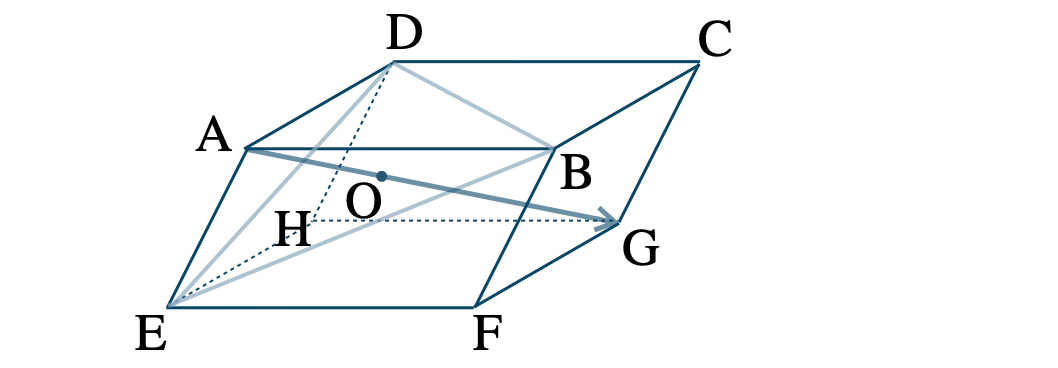
\( \overrightarrow{\rm AB}=\overrightarrow{a}~,~\overrightarrow{\rm AD}=\overrightarrow{b}~,~\overrightarrow{\rm AE}=\overrightarrow{c} \) とおくと、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CG}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AE}
\\[5pt]~~~&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
また、\( \triangle {\rm BDE} \) の重心が \( \rm O \) であることより、
\(\begin{eqnarray}~~~\overrightarrow{\rm AO}&=&\displaystyle \frac{\,\overrightarrow{\rm AD}+\overrightarrow{\rm AB}+\overrightarrow{\rm AE}\,}{\,3\,}
\\[5pt]~~~&=&\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})~ ~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\(\small [\,1\,]\) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}
\\[5pt]~~~&=&\displaystyle \frac{\,3\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&3\cdot\displaystyle \frac{\,1\,}{\,3\,}(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})
\\[5pt]~~~&=&3\overrightarrow{\rm AO}\hspace{30pt}(\,∵~ {\small [\,2\,]}\,)
\end{eqnarray}\)
したがって、\( \overrightarrow{\rm AG}=3\overrightarrow{\rm AO} \) より、
3点 \( \rm A~,~\rm O~,~\rm G \) は一直線上にある [終]
また、\( \rm AO:OG\) は、
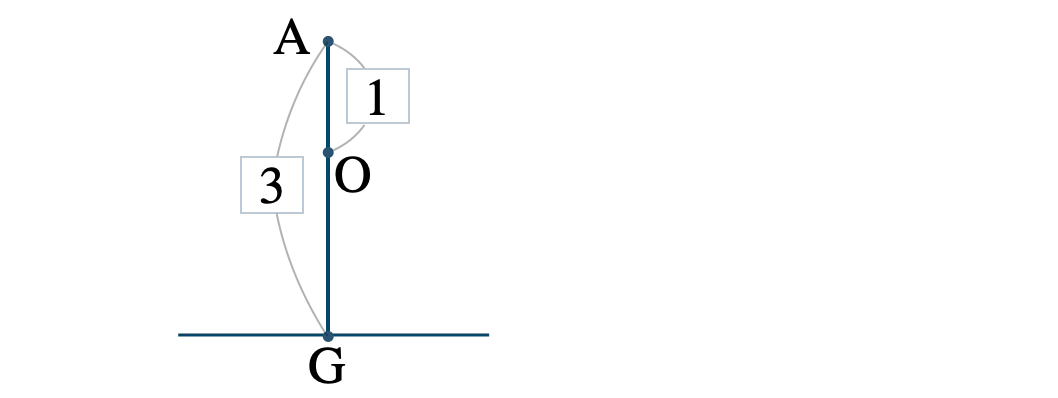

これより、\( \rm AO:OG=1:2 \) となる



