- 数学Ⅱ|複素数と方程式「複素数範囲の文字係数の2次方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|複素数範囲の文字係数の2次方程式
複素数と方程式 13\( m \) を定数とする2次方程式 \( x^2+mx+m=0 \) の解の種類の判別方法は?また、重解をもつ条件とそのときの重解の求め方は?
高校数学Ⅱ|複素数と方程式
解法のPoint
複素数範囲の文字係数の2次方程式
Point:複素数範囲の文字係数の2次方程式
\( ax^2+bx+c=0 \)
① 判別式 \( D=b^2-4ac \) を求める。
② 解の種類より、判別式 \( D \) の条件式を解く。
\({\small [\,1\,]}\) 異なる2つの実数解 \( \Leftrightarrow \) \( D \gt 0 \)
\({\small [\,2\,]}\) 重解 \( \Leftrightarrow \) \( D=0 \)
\({\small [\,3\,]}\) 異なる2つの虚数解 \( \Leftrightarrow \) \( D \lt 0 \)
文字係数の2次方程式の解の種類は、
\( ax^2+bx+c=0 \)
① 判別式 \( D=b^2-4ac \) を求める。
② 解の種類より、判別式 \( D \) の条件式を解く。
\({\small [\,1\,]}\) 異なる2つの実数解 \( \Leftrightarrow \) \( D \gt 0 \)
\({\small [\,2\,]}\) 重解 \( \Leftrightarrow \) \( D=0 \)
\({\small [\,3\,]}\) 異なる2つの虚数解 \( \Leftrightarrow \) \( D \lt 0 \)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|複素数範囲の文字係数の2次方程式
複素数と方程式 13
\( m \) を定数とする2次方程式 \( x^2+mx+m=0 \) の解の種類の判別方法は?また、重解をもつ条件とそのときの重解の求め方は?
高校数学Ⅱ|複素数と方程式
複素数範囲で、\( x^2+mx+m=0 \) の判別式を \( D \) とすると、
\(\begin{eqnarray}~~~D&=&m^2-4 \cdot 1 \cdot m
\\[3pt]~~~&=&m^2-4m\end{eqnarray}\)
\({\small [\,1\,]}\) \( D \gt 0 \) のとき、
\(\begin{eqnarray}~~~m^2-4m&\gt&0
\\[3pt]~~~m(m-4)&\gt&0\end{eqnarray}\)


\( m \lt 0~,~4 \lt m \)
このとき、異なる2つの実数解をもつ
\({\small [\,2\,]}\) \( D=0 \) のとき、
\(\begin{eqnarray}~~~m^2-4m&=&0
\\[3pt]~~~m(m-4)&=&0\end{eqnarray}\)
\( m=0~,~4 \)
このとき、重解をもつ
\({\small [\,3\,]}\) \( D \lt 0 \) のとき、
\(\begin{eqnarray}~~~m^2-4m&\lt&0
\\[3pt]~~~m(m-4)&\lt&0\end{eqnarray}\)
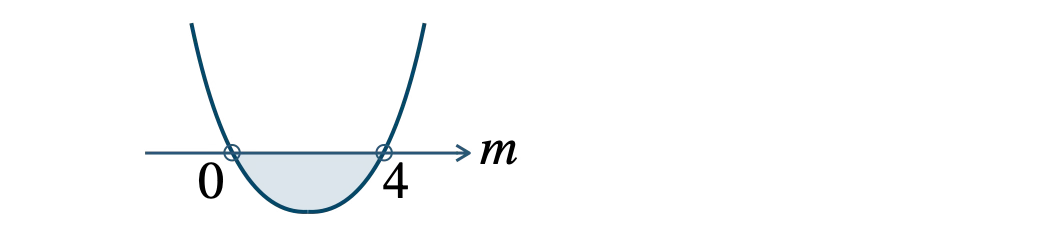

\( 0 \lt m \lt 4 \)
このとき、異なる2つの虚数解をもつ
また、重解をもつ条件は \( m=0~,~4 \) のときで、
\({\small (1)}~\)\( m=0 \) のとき、2次方程式は、
\( x^2=0 \) より、重解は \( x=0 \)
\({\small (2)}~\)\( m=4 \) のとき、2次方程式は、
\(\begin{eqnarray}~~~x^2+4x+4&=&0
\\[3pt]~~~(x+2)^2&=&0
\\[3pt]~~~x&=&-2\end{eqnarray}\)
よって、重解は \( x=-2 \) となる



