2次方程式の2つの解がともにkより大きい

\( x^2-mx+2=0 \) の判別式を \( D \) とすると

---

\(\begin{eqnarray}~~~D&=&(-m)^2-4 \cdot 1 \cdot 2\\[3pt]~~~&=&m^2-8~~~\cdots {\small [\,1\,]}\end{eqnarray}\)

---

また、解と係数の関係より、

---

　\(\left\{~\begin{array}{l} \alpha+\beta=-\displaystyle \frac{\,-m\,}{\,1\,}=m~~~\cdots {\small [\,2\,]}\\ \alpha\beta=\displaystyle \frac{\,2\,}{\,1\,}=2~~~\hspace{35pt}\cdots {\small [\,3\,]} \end{array}\right.\)

---

ここで、2つの解 \( \alpha~,~\beta \) がともに \( 1 \) より大きいとき、

---

　\( D \gt 0 \) かつ \( \alpha \gt 1 \) かつ \( \beta \gt 1 \)

---

　\( \Leftrightarrow \) \( D \gt 0 \) かつ \( \alpha-1 \gt 0 \) かつ \( \beta-1 \gt 0 \)

---

これより、2つの解 \( \alpha-1~,~\beta-1 \) がともに正の数と考えられるので、その条件は、

---

　\(\left\{~\begin{array}{l} D \gt 0 \\[3pt] (\alpha-1)+(\beta-1) \gt 0 \\[3pt] (\alpha-1)(\beta-1) \gt 0 \end{array}\right.\)

---

　\( D \gt 0 \) と \({\small [\,1\,]}\) より、

---

　\(\begin{eqnarray}~~~m^2-8& \gt &0
\\[3pt]~~~(m+2\sqrt{2})(m-2\sqrt{2})& \gt &0\end{eqnarray}\)

---

　よって、\(m\lt -2\sqrt{2}~,~2\sqrt{2} \lt m\)

---

　また、\( (\alpha-1)+(\beta-1) \gt 0 \) より、

---

　\(\begin{eqnarray}~~~\alpha+\beta-2& \gt &0
\\[3pt]~~~m-2& \gt &0\hspace{15pt}(\,∵~ {\small [\,2\,]}\,)
\\[3pt]~~~m& \gt &2\end{eqnarray}\)

---

　また、\( (\alpha-1)(\beta-1) \gt 0 \) より、

---

　\(\begin{eqnarray}~~~\alpha\beta-\alpha-\beta+1& \gt &0
\\[3pt]~~~\alpha\beta-(\alpha+\beta)+1& \gt &0
\\[3pt]~~~2-m+1& \gt &0\hspace{15pt}(\,∵~ {\small [\,2\,]}~,~{\small [\,3\,]}\,)
\\[3pt]~~~-m& \gt &-3
\\[3pt]~~~m& \lt &3\end{eqnarray}\)

---

数直線上にまとめると、

---

---

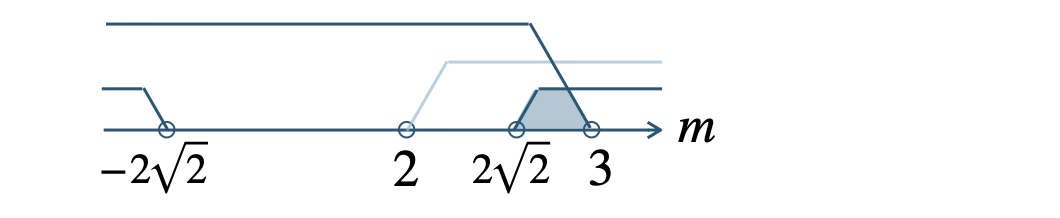
共通範囲より、\( 2\sqrt{2} \lt m \lt 3 \)