- 数学Ⅱ|図形と方程式「直線上の内分点・外分点・中点・線分の長さ」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|直線上の内分点・外分点・中点・線分の長さ
高校数学Ⅱ|図形と方程式
解法のPoint
直線上の内分点・外分点・中点・線分の長さ
直線上の2点 \({\rm A}(a)\),\({\rm B}(b)\) において、
■ 線分 \({\rm AB}\) を \(m:n\) に内分する点 \({\rm P}\) は、


\(\displaystyle \frac{\,na+mb\,}{\,m+n\,}\)
■ 線分 \({\rm AB}\) を \(m:n\) に外分する点 \({\rm Q}\) は、
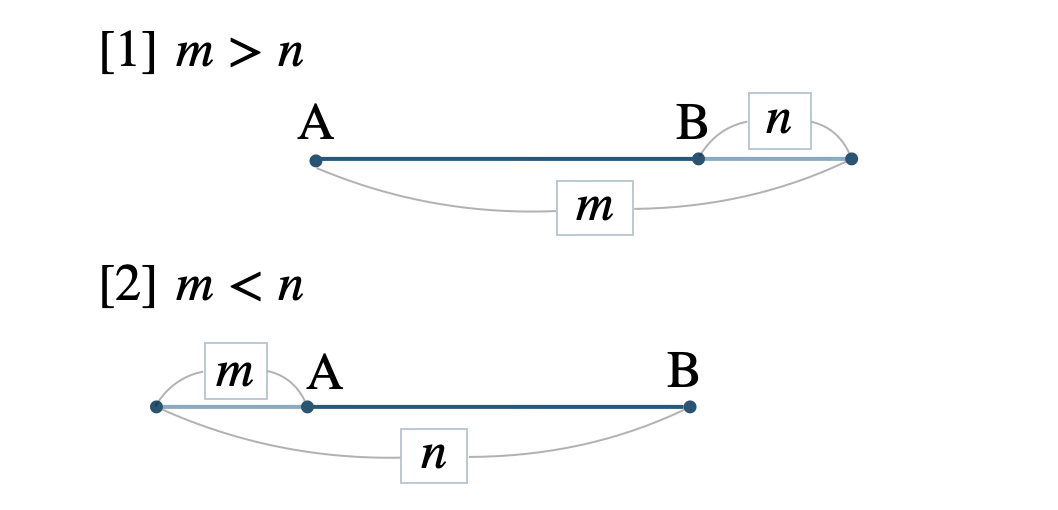

\(\displaystyle \frac{\,-na+mb\,}{\,m-n\,}\)
※ 内分点の式の比のどちらかにマイナスを付けて、\(m:-n\) と考える。
■ 線分 \({\rm AB}\) の中点 \({\rm M}\) は、


\(\displaystyle \frac{\,a+b\,}{\,2\,}\)
■ 線分 \({\rm AB}\) の長さは、
\({\rm AB}=|\,b-a\,|\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|直線上の内分点・外分点・中点・線分の長さ
2点 \({\rm A}(-4)\),\({\rm B}(2)\) を結ぶ線分 \({\rm AB}\) の \(2:1\) の内分点、\(2:1\) の外分点、中点の座標の求め方は?また、線分 \({\rm AB}\) の長さは?
高校数学Ⅱ|図形と方程式
線分 \({\rm AB}\) の \(2:1\) の内分点は、


\(\begin{eqnarray}~~~&&\displaystyle \frac{\,1 \cdot (-4)+2 \cdot 2\,}{\,2+1\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-4+4\,}{\,3\,}
\\[5pt]~~~&=&0\end{eqnarray}\)
線分 \({\rm AB}\) の \(2:1\) の外分点は、


\(\begin{eqnarray}~~~&&\displaystyle \frac{\,-1 \cdot (-4)+2 \cdot 2\,}{\,2+(-1)\,}
\\[5pt]~~~&=&\displaystyle \frac{\,4+4\,}{\,2-1\,}
\\[5pt]~~~&=&8\end{eqnarray}\)
線分 \({\rm AB}\) の中点は、


\(\begin{eqnarray}~~~&&\displaystyle \frac{\,-4+2\,}{\,2\,}
\\[5pt]~~~&=&\displaystyle \frac{\,-2\,}{\,2\,}
\\[5pt]~~~&=&-1\end{eqnarray}\)
線分 \({\rm AB}\) の長さは、
\(\begin{eqnarray}~~~&&|\,2-(-4)\,|
\\[3pt]~~~&=&|\,2+4\,|
\\[3pt]~~~&=&|\,6\,|
\\[3pt]~~~&=&6\end{eqnarray}\)


