- 数学Ⅱ|図形と方程式「平面上の3点の座標と三角形の形状」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|平面上の3点の座標と三角形の形状
図形と方程式 04平面上の3点 \({\rm A}(2~,~3)~,~\)\({\rm B}(-1~,~1)~,~\)\({\rm C}(1~,~-2)\) を結ぶ三角形の形状の調べ方は?
高校数学Ⅱ|図形と方程式
解法のPoint
平面上の3点の座標と三角形の形状
Point:平面上の3点の座標と三角形の形状
① 3つの辺 \({\rm AB}~,~\)\({\rm BC}~,~\)\({\rm CA}\) の長さを2点間の距離から求める。
② 長さが等しい条件と三平方の定理から、三角形の形状を決定する。
\({\small [\,1\,]}\) 3辺が等しい \({\rm AB}={\rm BC}={\rm CA}\)
\(\triangle{\rm ABC}\) は正三角形
\({\small [\,2\,]}\) 2辺が等しい \({\rm AB}={\rm BC}\)
\({\rm AB}={\rm BC}\) の二等辺三角形
\({\small [\,3\,]}\) 三平方の定理が成り立つ
\({\rm CA}^2={\rm AB}^2+{\rm BC}^2\)
\({\rm CA}\) を斜辺とする直角三角形
頂点の座標から三角形の形状を決定する方法は、
① 3つの辺 \({\rm AB}~,~\)\({\rm BC}~,~\)\({\rm CA}\) の長さを2点間の距離から求める。
② 長さが等しい条件と三平方の定理から、三角形の形状を決定する。
\({\small [\,1\,]}\) 3辺が等しい \({\rm AB}={\rm BC}={\rm CA}\)
\(\triangle{\rm ABC}\) は正三角形
\({\small [\,2\,]}\) 2辺が等しい \({\rm AB}={\rm BC}\)
\({\rm AB}={\rm BC}\) の二等辺三角形
\({\small [\,3\,]}\) 三平方の定理が成り立つ
\({\rm CA}^2={\rm AB}^2+{\rm BC}^2\)
\({\rm CA}\) を斜辺とする直角三角形
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|平面上の3点の座標と三角形の形状
図形と方程式 04
平面上の3点 \({\rm A}(2~,~3)~,~\)\({\rm B}(-1~,~1)~,~\)\({\rm C}(1~,~-2)\) を結ぶ三角形の形状の調べ方は?
高校数学Ⅱ|図形と方程式
辺 \({\rm AB}\) の長さは、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

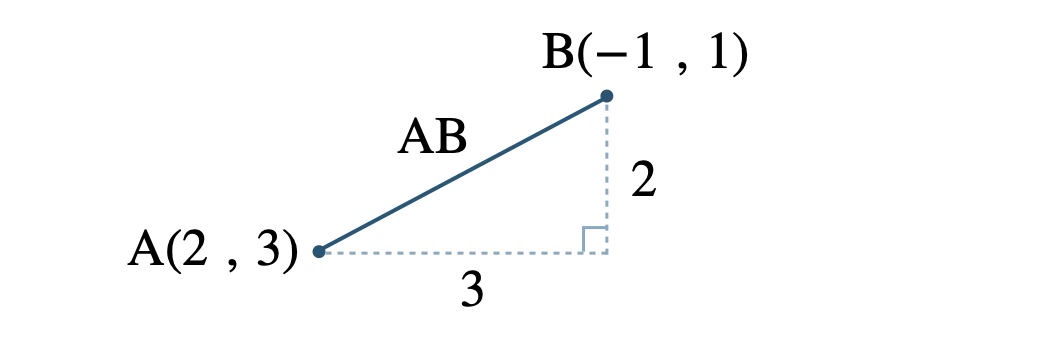


\(x\) 座標の差が \(|\,-1-2\,|=|\,-3\,|=3\)
\(y\) 座標の差が \(|\,1-3\,|=|\,-2\,|=2\)
よって、
\(\begin{eqnarray}~~~{\rm AB}&=&\sqrt{3^2+2^2}
\\[3pt]~~~&=&\sqrt{9+4}
\\[3pt]~~~&=&\sqrt{13}\end{eqnarray}\)
辺 \({\rm BC}\) の長さは、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

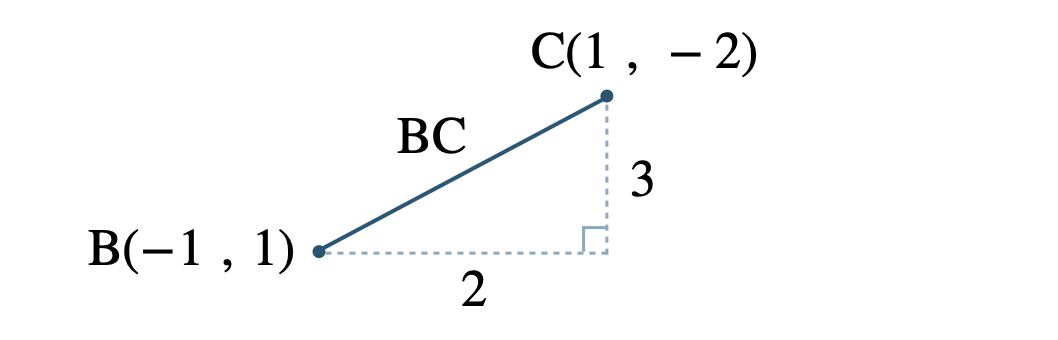


\(x\) 座標の差が \(|\,1-(-1)\,|=|\,2\,|=2\)
\(y\) 座標の差が \(|\,-2-1\,|=|\,-3\,|=3\)
よって、
\(\begin{eqnarray}~~~{\rm BC}&=&\sqrt{2^2+3^2}
\\[3pt]~~~&=&\sqrt{4+9}
\\[3pt]~~~&=&\sqrt{13}\end{eqnarray}\)
辺 \({\rm CA}\) の長さは、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

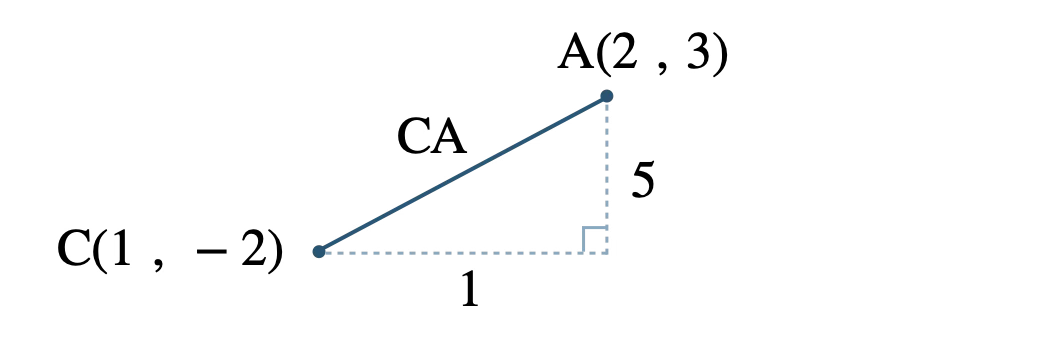


\(x\) 座標の差が \(|\,2-1\,|=|\,1\,|=1\)
\(y\) 座標の差が \(|\,3-(-2)\,|=|\,5\,|=5\)
よって、
\(\begin{eqnarray}~~~{\rm CA}&=&\sqrt{1^2+5^2}
\\[3pt]~~~&=&\sqrt{1+25}
\\[3pt]~~~&=&\sqrt{26}\end{eqnarray}\)
以上より、
\({\rm AB}={\rm BC}=\sqrt{13}\) より、
\({\rm AB}={\rm BC}\) の二等辺三角形
また、\({\rm CA}^2=26\) と
\({\rm AB}^2+{\rm BC}^2=13+13=26\) より、
\({\rm CA}^2={\rm AB}^2+{\rm BC}^2\) が成り立つので、
\({\rm CA}\) を斜辺とする直角三角形
したがって、\(\triangle{\rm ABC}\) は
\({\rm AB}={\rm BC}\) で \({\rm CA}\) を斜辺とする
直角二等辺三角形となる



