- 数学Ⅱ|図形と方程式「平面上の点に関して対称な点」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|平面上の点に関して対称な点
図形と方程式 08平面上の点 \({\rm A}(2~,~3)\) に関して点 \({\rm P}(0~,~-1)\) と対称な点 \({\rm Q}\) の座標の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
平面上の点に関して対称な点
Point:平面上の点に関して対称な点
点 \({\rm A}\) が線分 \({\rm PQ}\) の中点となる。


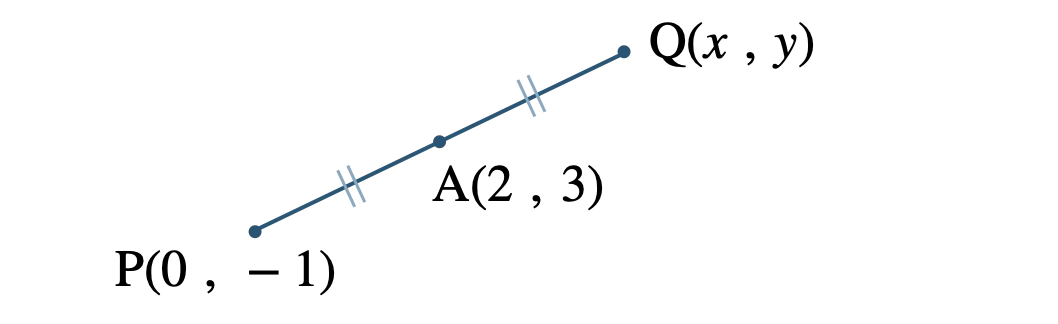
① 点 \({\rm Q}\) の座標を \((x~,~y)\) とし、線分 \({\rm PQ}\) の中点を求める。
② この中点が点 \({\rm A}\) と一致することより、\(x~,~y\) の値を求める。
点 \({\rm A}\) に関して、点 \({\rm P}\) と対称な点 \({\rm Q}\) の座標は、
点 \({\rm A}\) が線分 \({\rm PQ}\) の中点となる。



① 点 \({\rm Q}\) の座標を \((x~,~y)\) とし、線分 \({\rm PQ}\) の中点を求める。
② この中点が点 \({\rm A}\) と一致することより、\(x~,~y\) の値を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|平面上の点に関して対称な点
図形と方程式 08
平面上の点 \({\rm A}(2~,~3)\) に関して点 \({\rm P}(0~,~-1)\) と対称な点 \({\rm Q}\) の座標の求め方は?
高校数学Ⅱ|図形と方程式
点 \({\rm A}\) に関して、点 \({\rm P}\) と対称な点が \({\rm Q}\) より、点 \({\rm A}\) は線分 \({\rm PQ}\) の中点となる



点 \({\rm Q}\) の座標を \((x~,~y)\) とおくと、
線分 \({\rm PQ}\) の中点の \(x\) 座標は、
\(\displaystyle \frac{\,0+x\,}{\,2\,}=\frac{\,x\,}{\,2\,}\)
\(y\) 座標は、
\(\displaystyle \frac{\,-1+y\,}{\,2\,}=\frac{\,y-1\,}{\,2\,}\)
よって、\(\displaystyle \left(\frac{\,x\,}{\,2\,}~,~\frac{\,y-1\,}{\,2\,}\right)\)
これが、点 \({\rm A}(2~,~3)\) と一致するので、
\(\begin{eqnarray}~~~\frac{\,x\,}{\,2\,}&=&2
\\[3pt]~~~x&=&4\end{eqnarray}\)
また、
\(\begin{eqnarray}~~~\frac{\,y-1\,}{\,2\,}&=&3
\\[3pt]~~~y-1&=&6
\\[3pt]~~~y&=&7\end{eqnarray}\)
したがって、\({\rm Q}(4~,~7)\) となる



