- 数学Ⅱ|図形と方程式「3点が一直線上にある条件」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|3点が一直線上にある条件
図形と方程式 14平面上の3点 \((2~,~3)~,~\)\((-4~,~6)~,~\)\((2a~,~a)\) が一直線上にあるときの定数 \(a\) の値の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
3点が一直線上にある条件
Point:3点が一直線上にある条件
① 2点の座標より、直線の式を求める。
\((2~,~3)~,~\)\((-4~,~6)\) より、\(y=-\displaystyle\frac{\,1\,}{\,2\,}x+4\)
② もう1点がこの直線を通ることより、座標を代入して定数 \(a\) を求める。
\((2a~,~a)\) より、
\(~~~a=-\displaystyle\frac{\,1\,}{\,2\,}\cdot 2a+4~\Leftrightarrow ~ a=2\)
3点が一直線上にある条件は、
① 2点の座標より、直線の式を求める。
\((2~,~3)~,~\)\((-4~,~6)\) より、\(y=-\displaystyle\frac{\,1\,}{\,2\,}x+4\)
② もう1点がこの直線を通ることより、座標を代入して定数 \(a\) を求める。
\((2a~,~a)\) より、
\(~~~a=-\displaystyle\frac{\,1\,}{\,2\,}\cdot 2a+4~\Leftrightarrow ~ a=2\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|3点が一直線上にある条件
図形と方程式 14
平面上の3点 \((2~,~3)~,~\)\((-4~,~6)~,~\)\((2a~,~a)\) が一直線上にあるときの定数 \(a\) の値の求め方は?
高校数学Ⅱ|図形と方程式
2点 \((2~,~3)~,~\)\((-4~,~6)\) を通る直線の方程式は、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

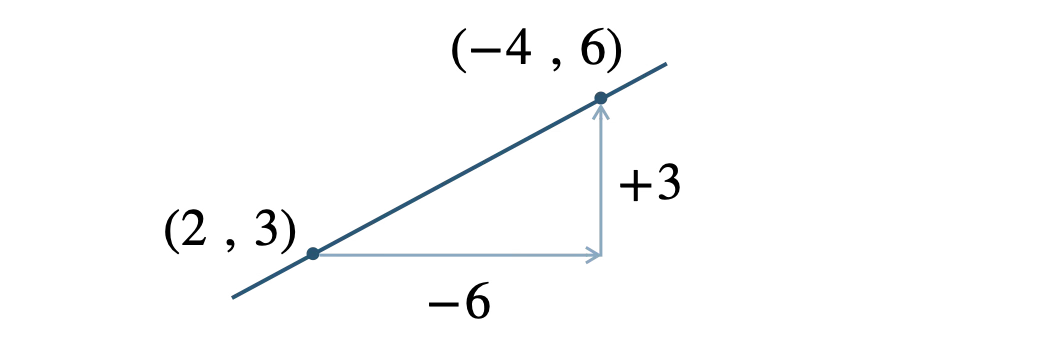


\(x\) の増加量が \(-4-2=-6\)
\(y\) の増加量が \(6-3=+3\)
これより、傾きが
\(\displaystyle\frac{\,3\,}{\,-6\,}=-\frac{\,1\,}{\,2\,}\)
点 \((2~,~3)\) を通るので、
\(\begin{eqnarray}~~~y-3&=&-\displaystyle\frac{\,1\,}{\,2\,}(x-2)
\\[3pt]~~~y&=&-\displaystyle\frac{\,1\,}{\,2\,}x+1+3
\\[3pt]~~~y&=&-\displaystyle\frac{\,1\,}{\,2\,}x+4\end{eqnarray}\)
この直線上に点 \((2a~,~a)\) があればよいので代入すると、
\(\begin{eqnarray}~~~a&=&-\displaystyle\frac{\,1\,}{\,2\,}\cdot 2a+4
\\[3pt]~~~a&=&-a+4
\\[3pt]~~~2a&=&4
\\[3pt]~~~a&=&2\end{eqnarray}\)
したがって、\(a=2\) となる



