- 数学Ⅱ|図形と方程式「垂直二等分線の方程式」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|垂直二等分線の方程式
図形と方程式 17☆2点 \({\rm A}(2~,~3)~,~\)\({\rm B}(-4~,~6)\) を結ぶ線分 \({\rm AB}\) の垂直二等分線の方程式の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
垂直二等分線の方程式
Point:垂直二等分線の方程式


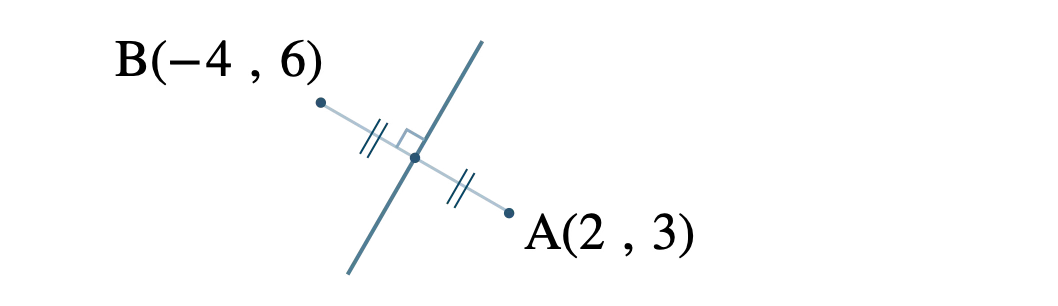
線分 \({\rm AB}\) の中点を通り、線分 \({\rm AB}\) に垂直である。
① 線分 \({\rm AB}\) の中点を求める。
\(\left(-1~,~\displaystyle\frac{\,9\,}{\,2\,}\right)\)
② 線分 \({\rm AB}\) の傾きを求め、傾きの積が \(-1\) より垂直二等分線の傾きを求める。
\(m{\, \small \times \,}\left(-\displaystyle\frac{\,1\,}{\,2\,}\right)=-1~~\Longleftrightarrow~~m=2\)
③ 中点の座標と傾きより、垂直二等分線の方程式を求める。
線分 \({\rm AB}\) の垂直二等分線の方程式は、



線分 \({\rm AB}\) の中点を通り、線分 \({\rm AB}\) に垂直である。
① 線分 \({\rm AB}\) の中点を求める。
\(\left(-1~,~\displaystyle\frac{\,9\,}{\,2\,}\right)\)
② 線分 \({\rm AB}\) の傾きを求め、傾きの積が \(-1\) より垂直二等分線の傾きを求める。
\(m{\, \small \times \,}\left(-\displaystyle\frac{\,1\,}{\,2\,}\right)=-1~~\Longleftrightarrow~~m=2\)
③ 中点の座標と傾きより、垂直二等分線の方程式を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|垂直二等分線の方程式
図形と方程式 17☆
2点 \({\rm A}(2~,~3)~,~\)\({\rm B}(-4~,~6)\) を結ぶ線分 \({\rm AB}\) の垂直二等分線の方程式の求め方は?
高校数学Ⅱ|図形と方程式

線分 \({\rm AB}\) の中点の \(x\) 座標は、
\(\displaystyle\frac{\,2+(-4)\,}{\,2\,}=\displaystyle\frac{\,-2\,}{\,2\,}=-1\)
\(y\) 座標は、
\(\displaystyle\frac{\,3+6\,}{\,2\,}=\displaystyle\frac{\,9\,}{\,2\,}\)
よって、\(\left(-1~,~\displaystyle\frac{\,9\,}{\,2\,}\right)\) となる
次に、線分 \({\rm AB}\) の傾きは、
下の図は実際の座標の位置関係とは異なるが、計算の手順を統一するために、常にこの形で図を描くとよい。

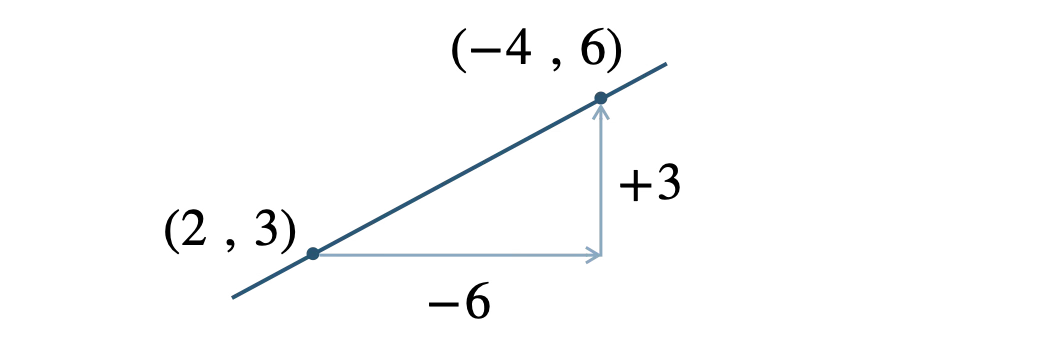


\(x\) 座標の差は \(-4-2=-6\)
\(y\) 座標の差は \(6-3=+3\)
よって、この直線の傾きは、
\(\displaystyle\frac{\,3\,}{\,-6\,}=-\displaystyle\frac{\,1\,}{\,2\,}\)
これより、垂直二等分線の傾きを \(m\) とすると、傾きの積が \(-1\) となることより、
\(\begin{eqnarray}~~~m{\, \small \times \,}\left(-\displaystyle\frac{\,1\,}{\,2\,}\right)&=&-1
\\[3pt]~~~m&=&2\end{eqnarray}\)
以上より、線分 \({\rm AB}\) の垂直二等分線は点 \(\left(-1~,~\displaystyle\frac{\,9\,}{\,2\,}\right)\) を通り、傾きが \(2\) であるので、
\(\begin{eqnarray}~~~y-\displaystyle\frac{\,9\,}{\,2\,}&=&2\left\{x-(-1)\right\}
\\[5pt]~~~2y-9&=&4(x+1)~~~\hspace{10pt} (\,∵~{\, \small \times \,} 2\,)
\\[3pt]~~~2y-9&=&4x+4
\\[3pt]~~~-4x+2y-9-4&=&0
\\[3pt]~~~-4x+2y-13&=&0
\\[3pt]~~~4x-2y+13&=&0\end{eqnarray}\)
したがって、\(4x-2y+13=0\) となる



