- 数学Ⅱ|図形と方程式「座標平面を用いた垂心の証明」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|座標平面を用いた垂心の証明
高校数学Ⅱ|図形と方程式
解法のPoint
座標平面を用いた垂心の証明
座標平面を用いて垂心の証明は、
① 辺 \({\rm BC}\) を \(x\) 軸、垂線 \({\rm AL}\) を \(y\) 軸、点 \({\rm L}\) を原点にとり、3つの頂点を \({\rm A}(0~,~a)~,~\)\({\rm B}(-b~,~0)~,~\)\({\rm C}(c~,~0)\) とおく。
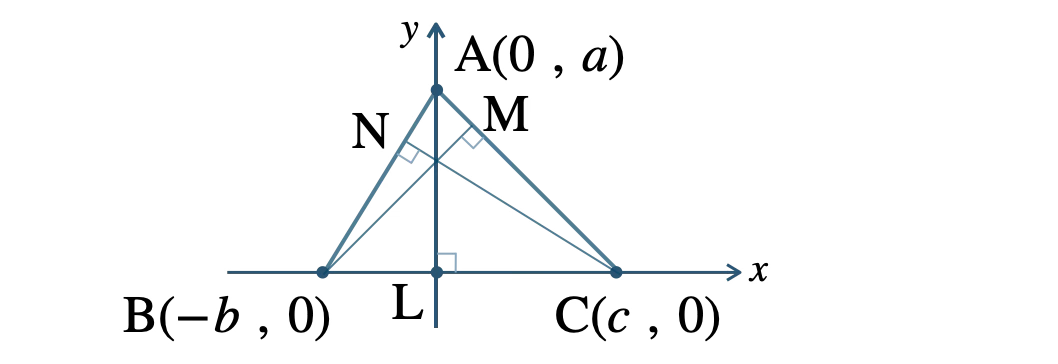


② 直線 \({\rm AB}\) の傾きより、垂線 \({\rm CN}\) の式を求め、直線 \({\rm AC}\) の傾きより、垂線 \({\rm BM}\) の式を求める。
③ 2本の垂線の \(y\) 軸との交点が一致して垂線 \({\rm AL}\) と交わることを示す。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|座標平面を用いた垂心の証明
\(\triangle{\rm ABC}\) の頂点から対辺に下ろした垂線 \({\rm AL}~,~\)\({\rm BM}~,~\)\({\rm CN}\) は1点で交わることの座標平面を用いた証明方法は?
高校数学Ⅱ|図形と方程式
[証明] 座標平面において、辺 \({\rm BC}\) を \(x\) 軸、垂線 \({\rm AL}\) を \(y\) 軸、点 \({\rm L}\) を原点 \((0~,~0)\) にとる
また、3つの頂点を \({\rm A}(0~,~a)~,~\)\({\rm B}(-b~,~0)~,~\)\({\rm C}(c~,~0)\) \(~~(\,a \neq 0\,)\) とおくと、



\({\small (1)}~\)\(b=0\) のとき、点 \({\rm B}\) と点 \({\rm L}\) が一致し、直角三角形となり、3本の垂線は頂点で交わる
\({\small (2)}~\)\(c=0\) のとき、点 \({\rm C}\) と点 \({\rm L}\) が一致し、直角三角形となり、3本の垂線は頂点で交わる
\({\small (3)}~\)\(b \neq 0\) かつ \(c \neq 0\) のとき、
直線 \({\rm AB}\) の傾きは \(\displaystyle\frac{\,a-0\,}{\,0-(-b)\,}=\frac{\,a\,}{\,b\,}\) より、
直線 \({\rm CN}\) の傾きは \(\displaystyle -\frac{\,b\,}{\,a\,}\) となる
\((\,∵~\)傾きの積が \(-1\,)\)
直線 \({\rm CN}\) は点 \({\rm C}(c~,~0)\) を通るので、
\(\begin{eqnarray}~~~y-0&=&\displaystyle -\frac{\,b\,}{\,a\,}(x-c)
\\[3pt]~~~y&=&\displaystyle -\frac{\,b\,}{\,a\,}x+\frac{\,bc\,}{\,a\,}~~~\cdots{\small [\,1\,]}\end{eqnarray}\)
次に、直線 \({\rm AC}\) の傾きは \(\displaystyle\frac{\,a-0\,}{\,0-c\,}=\displaystyle -\frac{\,a\,}{\,c\,}\) より、
直線 \({\rm BM}\) の傾きは \(\displaystyle \frac{\,c\,}{\,a\,}\) となる
\((\,∵~\)傾きの積が \(-1\,)\)
直線 \({\rm BM}\) は点 \({\rm B}(-b~,~0)\) を通るので、
\(\begin{eqnarray}~~~y-0&=&\displaystyle \frac{\,c\,}{\,a\,}\left\{x-(-b)\right\}
\\[3pt]~~~y&=&\displaystyle \frac{\,c\,}{\,a\,}x+\frac{\,bc\,}{\,a\,}~~~\cdots{\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) はともに \(y\) 軸との交点 \(\displaystyle {\rm H}\left(0~,~\frac{\,bc\,}{\,a\,}\right)\) を通り、直線 \({\rm AL}\) も \(y\) 軸上の点 \({\rm H}\) を通る
したがって、3本の垂線は1点で交わる [終]
※ 教科書では \({\rm B}(b~,~0)~~(\,b\lt 0\,)\) と置いているが、\({\rm B}(-b~,~0)~~(\,b\gt 0\,)\) と置く方が点の位置が直感的にわかりやすい。



