- 数学Ⅱ|図形と方程式「直線に関して点と対称な点の座標」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|直線に関して点と対称な点の座標
図形と方程式 24直線 \(x-2y+2=0\) に関して、点 \({\rm A}(1~,~4)\) と対称な点 \({\rm B}\) の座標の求め方は?
高校数学Ⅱ|図形と方程式
解法のPoint
直線に関して点と対称な点の座標
Point:直線に関して点と対称な点の座標


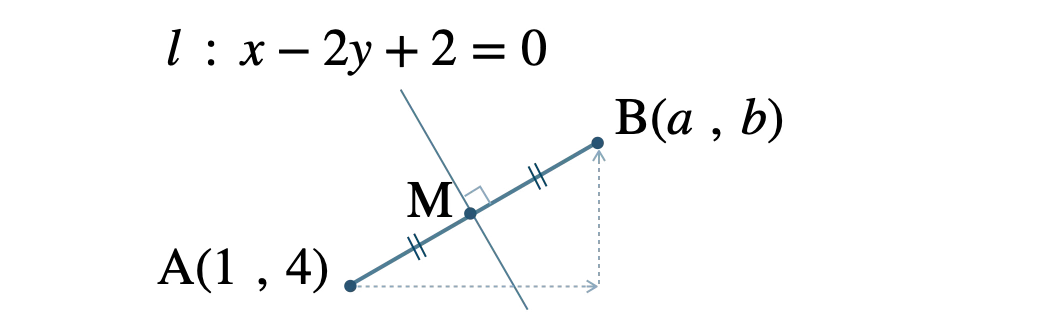
\({\small [\,1\,]}\) 直線 \(l\) と直線 \({\rm AB}\) が垂直。
\({\small [\,2\,]}\) 線分 \({\rm AB}\) の中点が直線 \(l\) 上にある。
① 点 \({\rm B}\) の座標を \((a~,~b)\) とおく。
② 直線 \(l\) と直線 \({\rm AB}\) の傾きを求めて、\({\small [\,1\,]}\) より傾きの積は \(-1\) となる式を立てる。
③ 線分 \({\rm AB}\) の中点の座標を求め、\({\small [\,2\,]}\) より直線 \(l\) に代入して式を立てる。
④ 2つの式を連立して点 \({\rm B}\) の座標を求める。
直線 \(l\) に関して点 \({\rm A}\) と対称な点 \({\rm B}\) の座標は、



\({\small [\,1\,]}\) 直線 \(l\) と直線 \({\rm AB}\) が垂直。
\({\small [\,2\,]}\) 線分 \({\rm AB}\) の中点が直線 \(l\) 上にある。
① 点 \({\rm B}\) の座標を \((a~,~b)\) とおく。
② 直線 \(l\) と直線 \({\rm AB}\) の傾きを求めて、\({\small [\,1\,]}\) より傾きの積は \(-1\) となる式を立てる。
③ 線分 \({\rm AB}\) の中点の座標を求め、\({\small [\,2\,]}\) より直線 \(l\) に代入して式を立てる。
④ 2つの式を連立して点 \({\rm B}\) の座標を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|直線に関して点と対称な点の座標
図形と方程式 24
直線 \(x-2y+2=0\) に関して、点 \({\rm A}(1~,~4)\) と対称な点 \({\rm B}\) の座標の求め方は?
高校数学Ⅱ|図形と方程式
直線 \(x-2y+2=0\) を \(l\) 、点 \({\rm B}\) の座標を \((a~,~b)\) とおくと、



直線 \(l\) の傾きは、
\(\begin{eqnarray}~~~x-2y+2&=&0
\\[3pt]~~~-2y&=&-x-2
\\[5pt]~~~y&=&\displaystyle\frac{\,1\,}{\,2\,}x+1\end{eqnarray}\)
よって、\(\displaystyle\frac{\,1\,}{\,2\,}\) である
また、直線 \({\rm AB}\) の傾きは、\(\displaystyle\frac{\,b-4\,}{\,a-1\,}\) であり、直線 \(l\) と直線 \({\rm AB}\) は垂直に交わるので、傾きの積は \(-1\) より、
\(\begin{eqnarray}~~~\displaystyle\frac{\,1\,}{\,2\,}\cdot\displaystyle\frac{\,b-4\,}{\,a-1\,}&=&-1
\\[5pt]~~~\displaystyle\frac{\,b-4\,}{\,2(a-1)\,}&=&-1
\\[5pt]~~~b-4&=&-2(a-1)
\\[3pt]~~~b-4&=&-2a+2
\\[3pt]~~~2a+b&=&2+4
\\[3pt]~~~2a+b&=&6~~~\cdots{\small [\,1\,]}\end{eqnarray}\)
次に、線分 \({\rm AB}\) の中点 \({\rm M}\) の座標は、
\({\rm M}\left(\displaystyle\frac{\,1+a\,}{\,2\,}~,~\displaystyle\frac{\,4+b\,}{\,2\,}\right)\)
この点 \({\rm M}\) は直線 \(l\) 上にあるので、\(x-2y+2=0\) に代入すると、
\(\begin{eqnarray}~~~\displaystyle\frac{\,1+a\,}{\,2\,}-2\cdot\displaystyle\frac{\,4+b\,}{\,2\,}+2&=&0
\\[5pt]~~~(1+a)-2(4+b)+2{\, \small \times \,} 2&=&0~~~(\,∵~{\, \small \times \,} 2\,)
\\[3pt]~~~1+a-8-2b+4&=&0
\\[3pt]~~~a-2b&=&3~~~\cdots{\small [\,2\,]}\end{eqnarray}\)
\({\small [\,1\,]}{\, \small \times \,} 2+{\small [\,2\,]}\) より、
\(\begin{eqnarray}~~~~~
4a+2b&=&12 \\~~
+\big{)}~~~a-2b&=&3\\
\hline 5a&=&15
\\[3pt] a&=&3\end{eqnarray}\)
\({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~2{\, \small \times \,} 3+b&=&6
\\[3pt]~~~6+b&=&6
\\[3pt]~~~b&=&0\end{eqnarray}\)
したがって、点 \({\rm B}\) の座標は \((3~,~0)\) となる



