このページは、「点と直線との距離と三角形の面積」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
点と直線との距離と三角形の面積 で確認できます。
問題アーカイブ01
\({\small (1)}~\)直線 \({\rm BC}\) の方程式
\({\small (2)}~\)線分 \({\rm BC}\) の長さ
\({\small (3)}~\)点 \({\rm A}\) と直線 \({\rm BC}\) の距離
\({\small (4)}~\)\(\triangle{\rm ABC}\) の面積
数研出版|数学Ⅱ[709] p.91 問題 7
2点 \({\rm B}(-3~,~-5)~,~\)\({\rm C}(5~,~-1)\) より、
\(x\) の増加量が \(5-(-3)=+8\)
\(y\) の増加量が \(-1-(-5)=+4\)
よって、傾きが \(\displaystyle\frac{\,+4\,}{\,+8\,}=\displaystyle\frac{\,1\,}{\,2\,}\)
これより、点 \({\rm B}(-3~,~-5)\) を通り傾き \(\displaystyle\frac{\,1\,}{\,2\,}\) の直線は、
\(\begin{eqnarray}~~~y-(-5)&=&\displaystyle\frac{\,1\,}{\,2\,}\{x-(-3)\}
\\[5pt]~y+5&=&\displaystyle\frac{\,1\,}{\,2\,}(x+3)
\\[5pt]~2(y+5)&=&x+3
\\[3pt]~2y+10&=&x+3
\\[3pt]~x-2y+3-10&=&0
\\[3pt]~x-2y-7&=&0\end{eqnarray}\)
したがって、\({\small (1)}~\)直線 \({\rm BC}\) の方程式は \(x-2y-7=0\)
次に、辺 \({\rm BC}\) の長さは、
\(x\) 座標の差が \(|\,5-(-3)\,|=8\)
\(y\) 座標の差が \(|\,-1-(-5)\,|=4\)
これより、
\(\begin{eqnarray}~{\rm BC}&=&\sqrt{8^2+4^2}
\\[3pt]~~~&=&\sqrt{64+16}
\\[3pt]~~~&=&\sqrt{80}
\\[3pt]~~~&=&4\sqrt{5}\end{eqnarray}\)
したがって、\({\small (2)}~\)線分 \({\rm BC}\) の長さは \(4\sqrt{5}\)
よって、点 \({\rm A}(-2~,~4)\) と直線 \({\rm BC}\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,1\cdot(-2)+(-2)\cdot4-7\,|\,}{\,\sqrt{1^2+(-2)^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-2-8-7\,|\,}{\,\sqrt{1+4}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-17\,|\,}{\,\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,17\,}{\,\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,17{\, \small \times \,}\sqrt{5}\,}{\,\sqrt{5}{\, \small \times \,}\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,17\sqrt{5}\,}{\,5\,}\end{eqnarray}\)
したがって、\({\small (3)}~\)点 \({\rm A}\) と直線 \({\rm BC}\) の距離は \(\displaystyle\frac{\,17\sqrt{5}\,}{\,5\,}\)
以上より、\(\triangle{\rm ABC}\) の面積は、辺 \({\rm BC}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm ABC}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}4\sqrt{5}{\, \small \times \,}\displaystyle\frac{\,17\sqrt{5}\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,4{\, \small \times \,}17{\, \small \times \,}5\,}{\,2{\, \small \times \,}5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,340\,}{\,10\,}=34\end{eqnarray}\)
したがって、\({\small (4)}~\)\(\triangle{\rm ABC}\) の面積は \(34\)
問題アーカイブ02
\({\small (1)}~\)点 \({\rm B}\) と直線 \({\rm OA}\) の距離を \(x_1~,~y_1~,~x_2~,~y_2\) を用いて表せ。
\({\small (2)}~\)\(\triangle{\rm OAB}\) の面積は、\(\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\) で表されることを示せ。
数研出版|数学Ⅱ[709] p.120 演習問題A 4
数研出版|高等学校数学Ⅱ[710] p.111 章末問題A 4
\({\small (1)}~\)直線 \({\rm OA}\) の方程式を求める。
2点 \({\rm O}(0~,~0)~,~\)\({\rm A}(x_1~,~y_1)\) より、
\(x\) の増加量が \(x_1-0=x_1\)
\(y\) の増加量が \(y_1-0=y_1\)
よって、傾きが \(\displaystyle\frac{\,y_1\,}{\,x_1\,}\)
これより、原点 \({\rm O}(0~,~0)\) を通り傾き \(\displaystyle\frac{\,y_1\,}{\,x_1\,}\) の直線は、
\(\begin{eqnarray}~~~y&=&\displaystyle\frac{\,y_1\,}{\,x_1\,}x
\\[5pt]~x_1y&=&y_1x
\\[3pt]~y_1x-x_1y&=&0\end{eqnarray}\)
よって、点 \({\rm B}(x_2~,~y_2)\) と直線 \({\rm OA}\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,y_1\cdot x_2+(-x_1)\cdot y_2\,|\,}{\,\sqrt{y_1^2+(-x_1)^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}\end{eqnarray}\)
したがって、点 \({\rm B}\) と直線 \({\rm OA}\) の距離は \(\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}\)
\({\small (2)}~\)[証明] 辺 \({\rm OA}\) の長さは、
\(x\) 座標の差が \(|\,x_1-0\,|=|\,x_1\,|\)
\(y\) 座標の差が \(|\,y_1-0\,|=|\,y_1\,|\)
これより、
\(\begin{eqnarray}~{\rm OA}&=&\sqrt{x_1^2+y_1^2}\end{eqnarray}\)
以上より、\(\triangle{\rm OAB}\) の面積は、辺 \({\rm OA}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm OAB}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm OA}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}\sqrt{x_1^2+y_1^2}{\, \small \times \,}\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\end{eqnarray}\)
したがって、\(\triangle{\rm OAB}\) の面積は \(\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\) で表される [終]
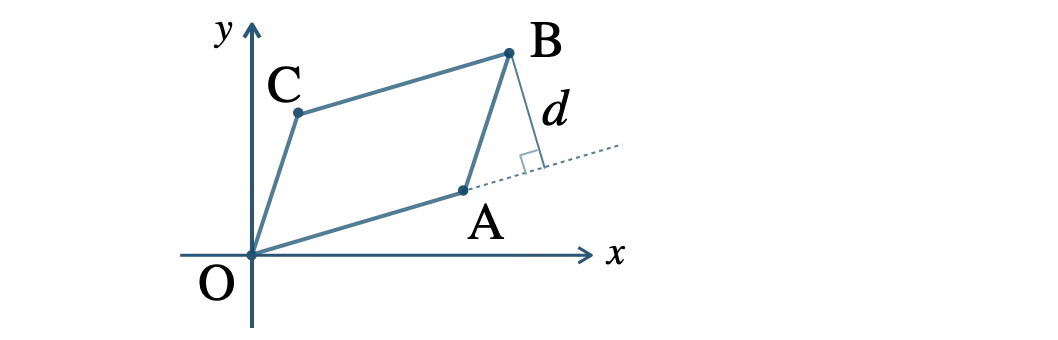
問題アーカイブ03
数研出版|数学Ⅱ[709] p.121 演習問題B 10
点 \({\rm B}\) は直線 \({\rm AB}\) と直線 \({\rm BC}\) の交点より、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
4x-y-14=0~\cdots {\small [\,1\,]}\\
x-2y+7=0~\cdots {\small [\,2\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,1\,]}\) より \(y=4x-14\) を \({\small [\,2\,]}\) に代入すると、
\(\begin{eqnarray}~~~x-2(4x-14)+7&=&0
\\[3pt]~x-8x+28+7&=&0
\\[3pt]~-7x+35&=&0
\\[3pt]~x&=&5\end{eqnarray}\)
\(y=4\cdot5-14=6\) より、点 \({\rm B}(5~,~6)\)
直線 \({\rm OA}\) の方程式は、
直線 \({\rm BC}\):\(x-2y+7=0\) より、傾きは \(\displaystyle\frac{\,1\,}{\,2\,}\)
よって、原点 \({\rm O}(0~,~0)\) を通り傾き \(\displaystyle\frac{\,1\,}{\,2\,}\) の直線は、
\(\begin{eqnarray}~~~y&=&\displaystyle\frac{\,1\,}{\,2\,}x
\\[5pt]~2y&=&x
\\[3pt]~x-2y&=&0\end{eqnarray}\)
点 \({\rm B}(5~,~6)\) と直線 \({\rm OA}\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,1\cdot5+(-2)\cdot6\,|\,}{\,\sqrt{1^2+(-2)^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,5-12\,|\,}{\,\sqrt{1+4}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-7\,|\,}{\,\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,7\,}{\,\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,7{\, \small \times \,}\sqrt{5}\,}{\,\sqrt{5}{\, \small \times \,}\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,7\sqrt{5}\,}{\,5\,}\end{eqnarray}\)
辺 \({\rm OA}\) の長さは、
点 \({\rm A}\) は直線 \({\rm AB}\) と直線 \({\rm OA}\) の交点なので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
4x-y-14=0~\cdots {\small [\,1\,]}\\
x-2y=0~\cdots {\small [\,3\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,3\,]}\) より \(x=2y\) を \({\small [\,1\,]}\) に代入すると、
\(\begin{eqnarray}~~~4\cdot2y-y-14&=&0
\\[3pt]~8y-y-14&=&0
\\[3pt]~7y&=&14
\\[3pt]~y&=&2\end{eqnarray}\)
\(x=2\cdot2=4\) より、点 \({\rm A}(4~,~2)\)
これより、
\(\begin{eqnarray}~{\rm OA}&=&\sqrt{4^2+2^2}
\\[3pt]~~~&=&\sqrt{16+4}
\\[3pt]~~~&=&\sqrt{20}
\\[3pt]~~~&=&2\sqrt{5}\end{eqnarray}\)
以上より、平行四辺形 \({\rm OABC}\) の面積は、辺 \({\rm OA}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~{\rm OABC}&=&{\rm OA}{\, \small \times \,}d
\\[5pt]~~~&=&2\sqrt{5}{\, \small \times \,}\displaystyle\frac{\,7\sqrt{5}\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,2{\, \small \times \,}7{\, \small \times \,}5\,}{\,5\,}
\\[5pt]~~~&=&14\end{eqnarray}\)
したがって、平行四辺形 \({\rm OABC}\) の面積は \(14\)
問題アーカイブ04
\({\small (1)}~\)2点 \({\rm A}(4~,~-2)~,~\)\({\rm B}(-2~,~6)\) を通る直線 \(\ell\) の方程式を求めよ。
\({\small (2)}~\)原点 \({\rm O}\) と直線 \(\ell\) の距離を求めよ。
\({\small (3)}~\)\(\triangle{\rm OAB}\) の面積を求めよ。
数研出版|高等学校数学Ⅱ[710] p.85 問題 8
\({\small (1)}~\)2点 \({\rm A}(4~,~-2)~,~\)\({\rm B}(-2~,~6)\) より、
\(x\) の増加量が \(-2-4=-6\)
\(y\) の増加量が \(6-(-2)=+8\)
よって、傾きが \(\displaystyle\frac{\,+8\,}{\,-6\,}=-\displaystyle\frac{\,4\,}{\,3\,}\)
これより、点 \({\rm A}(4~,~-2)\) を通り傾き \(-\displaystyle\frac{\,4\,}{\,3\,}\) の直線は、
\(\begin{eqnarray}~~~y-(-2)&=&-\displaystyle\frac{\,4\,}{\,3\,}(x-4)
\\[5pt]~y+2&=&-\displaystyle\frac{\,4\,}{\,3\,}(x-4)
\\[5pt]~3(y+2)&=&-4(x-4)
\\[3pt]~3y+6&=&-4x+16
\\[3pt]~4x+3y+6-16&=&0
\\[3pt]~4x+3y-10&=&0\end{eqnarray}\)
したがって、直線 \(\ell\) の方程式は \(4x+3y-10=0\)
\({\small (2)}~\)原点 \({\rm O}(0~,~0)\) と直線 \(\ell\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,4\cdot0+3\cdot0-10\,|\,}{\,\sqrt{4^2+3^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-10\,|\,}{\,\sqrt{16+9}\,}
\\[5pt]~&=&\displaystyle\frac{\,10\,}{\,\sqrt{25}\,}
\\[5pt]~&=&\displaystyle\frac{\,10\,}{\,5\,}=2\end{eqnarray}\)
したがって、原点 \({\rm O}\) と直線 \(\ell\) の距離は \(2\)
\({\small (3)}~\)辺 \({\rm AB}\) の長さは、
\(x\) 座標の差が \(|\,-2-4\,|=6\)
\(y\) 座標の差が \(|\,6-(-2)\,|=8\)
これより、
\(\begin{eqnarray}~{\rm AB}&=&\sqrt{6^2+8^2}
\\[3pt]~~~&=&\sqrt{36+64}
\\[3pt]~~~&=&\sqrt{100}
\\[3pt]~~~&=&10\end{eqnarray}\)
以上より、\(\triangle{\rm OAB}\) の面積は、辺 \({\rm AB}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm OAB}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm AB}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}10{\, \small \times \,}2
\\[5pt]~~~&=&10\end{eqnarray}\)
したがって、\(\triangle{\rm OAB}\) の面積は \(10\)
問題アーカイブ05
\({\small (1)}~\)2直線 \(x-y+1=0~,~2x+y-7=0\) の交点 \({\rm A}\) の座標を求めよ。
\({\small (2)}~\)\({\small (1)}\) の点 \({\rm A}\) と直線 \(x+2y-5=0\) の距離を求めよ。
\({\small (3)}~\)3つの直線で囲まれた三角形の面積を求めよ。
数研出版|新編数学Ⅱ[711] p.108 章末問題A 3
\({\small (1)}~\)2直線 \(x-y+1=0~,~2x+y-7=0\) の交点 \({\rm A}\) を求める。
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
x-y+1=0~\cdots {\small [\,1\,]}\\
2x+y-7=0~\cdots {\small [\,2\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,1\,]}+{\small [\,2\,]}\) より、
\(\begin{eqnarray}~~~~~
x-y+1&=&0 \\~~
+\big{)}~~~2x+y-7&=&0\\
\hline 3x-6&=&0
\\[3pt] x&=&2\end{eqnarray}\)
\({\small [\,1\,]}\) に代入すると、\(2-y+1=0\) より \(y=3\)
したがって、交点 \({\rm A}\) の座標は \((2~,~3)\)
\({\small (2)}~\)点 \({\rm A}(2~,~3)\) と直線 \(x+2y-5=0\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,1\cdot2+2\cdot3-5\,|\,}{\,\sqrt{1^2+2^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,2+6-5\,|\,}{\,\sqrt{1+4}\,}
\\[5pt]~&=&\displaystyle\frac{\,3\,}{\,\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,3{\, \small \times \,}\sqrt{5}\,}{\,\sqrt{5}{\, \small \times \,}\sqrt{5}\,}
\\[5pt]~&=&\displaystyle\frac{\,3\sqrt{5}\,}{\,5\,}\end{eqnarray}\)
したがって、点 \({\rm A}\) と直線 \(x+2y-5=0\) の距離は \(\displaystyle\frac{\,3\sqrt{5}\,}{\,5\,}\)
\({\small (3)}~\)3つの直線で囲まれた三角形の残りの頂点は、
点 \({\rm B}\) は直線 \(x-y+1=0\) と直線 \(x+2y-5=0\) の交点なので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
x-y+1=0~\cdots {\small [\,1\,]}\\
x+2y-5=0~\cdots {\small [\,3\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,3\,]}-{\small [\,1\,]}\) より、\(3y-6=0\) なので \(y=2\)
\({\small [\,1\,]}\) に代入すると、\(x-2+1=0\) より \(x=1\)
よって、点 \({\rm B}(1~,~2)\)
点 \({\rm C}\) は直線 \(2x+y-7=0\) と直線 \(x+2y-5=0\) の交点なので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
2x+y-7=0~\cdots {\small [\,2\,]}\\
x+2y-5=0~\cdots {\small [\,3\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,2\,]}-2{\, \small \times \,}{\small [\,3\,]}\) より、\(-3y+3=0\) なので \(y=1\)
\({\small [\,3\,]}\) に代入すると、\(x+2-5=0\) より \(x=3\)
よって、点 \({\rm C}(3~,~1)\)
辺 \({\rm BC}\) の長さは、
\(x\) 座標の差が \(|\,3-1\,|=2\)
\(y\) 座標の差が \(|\,1-2\,|=1\)
これより、
\(\begin{eqnarray}~{\rm BC}&=&\sqrt{2^2+1^2}
\\[3pt]~~~&=&\sqrt{4+1}
\\[3pt]~~~&=&\sqrt{5}\end{eqnarray}\)
以上より、三角形の面積は、辺 \({\rm BC}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm ABC}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm BC}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}\sqrt{5}{\, \small \times \,}\displaystyle\frac{\,3\sqrt{5}\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,3{\, \small \times \,}5\,}{\,2{\, \small \times \,}5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,3\,}{\,2\,}\end{eqnarray}\)
したがって、3つの直線で囲まれた三角形の面積は \(\displaystyle\frac{\,3\,}{\,2\,}\)
問題アーカイブ06
\({\small (1)}~\)線分 \({\rm AB}\) の長さを求めよ。
\({\small (2)}~\)\(\triangle{\rm OAB}\) の面積を求めよ。
東京書籍|Advanced数学Ⅱ[701] p.110 練習問題A 3
点 \({\rm A}\) は直線 \(2x+3y-11=0\) と直線 \(y=\displaystyle\frac{\,1\,}{\,4\,}x\) の交点なので、
\(y=\displaystyle\frac{\,1\,}{\,4\,}x\) を \(2x+3y-11=0\) に代入すると、
\(\begin{eqnarray}~~~2x+3\cdot\displaystyle\frac{\,1\,}{\,4\,}x-11&=&0
\\[5pt]~2x+\displaystyle\frac{\,3\,}{\,4\,}x-11&=&0
\\[5pt]~\displaystyle\frac{\,8\,}{\,4\,}x+\displaystyle\frac{\,3\,}{\,4\,}x&=&11
\\[5pt]~\displaystyle\frac{\,11\,}{\,4\,}x&=&11
\\[5pt]~x&=&4\end{eqnarray}\)
\(y=\displaystyle\frac{\,1\,}{\,4\,}\cdot4=1\) より、点 \({\rm A}(4~,~1)\)
点 \({\rm B}\) は直線 \(2x+3y-11=0\) と直線 \(y=3x\) の交点なので、
\(y=3x\) を \(2x+3y-11=0\) に代入すると、
\(\begin{eqnarray}~~~2x+3\cdot3x-11&=&0
\\[3pt]~2x+9x-11&=&0
\\[3pt]~11x&=&11
\\[3pt]~x&=&1\end{eqnarray}\)
\(y=3\cdot1=3\) より、点 \({\rm B}(1~,~3)\)
\({\small (1)}~\)辺 \({\rm AB}\) の長さは、
\(x\) 座標の差が \(|\,4-1\,|=3\)
\(y\) 座標の差が \(|\,1-3\,|=2\)
これより、
\(\begin{eqnarray}~~~{\rm AB}&=&\sqrt{3^2+2^2}
\\[3pt]~~~&=&\sqrt{9+4}
\\[3pt]~~~&=&\sqrt{13}\end{eqnarray}\)
したがって、線分 \({\rm AB}\) の長さは \(\sqrt{13}\)
\({\small (2)}~\)原点 \({\rm O}(0~,~0)\) と直線 \(2x+3y-11=0\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,2\cdot0+3\cdot0-11\,|\,}{\,\sqrt{2^2+3^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-11\,|\,}{\,\sqrt{4+9}\,}
\\[5pt]~&=&\displaystyle\frac{\,11\,}{\,\sqrt{13}\,}
\\[5pt]~&=&\displaystyle\frac{\,11{\, \small \times \,}\sqrt{13}\,}{\,\sqrt{13}{\, \small \times \,}\sqrt{13}\,}
\\[5pt]~&=&\displaystyle\frac{\,11\sqrt{13}\,}{\,13\,}\end{eqnarray}\)
以上より、\(\triangle{\rm OAB}\) の面積は、辺 \({\rm AB}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm OAB}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm AB}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}\sqrt{13}{\, \small \times \,}\displaystyle\frac{\,11\sqrt{13}\,}{\,13\,}
\\[5pt]~~~&=&\displaystyle\frac{\,11{\, \small \times \,}13\,}{\,2{\, \small \times \,}13\,}
\\[5pt]~~~&=&\displaystyle\frac{\,11\,}{\,2\,}\end{eqnarray}\)
したがって、\(\triangle{\rm OAB}\) の面積は \(\displaystyle\frac{\,11\,}{\,2\,}\)
問題アーカイブ07
\({\small (1)}~\)線分 \({\rm OA}\) の長さを求めよ。
\({\small (2)}~\)点 \({\rm B}\) と直線 \({\rm OA}\) の距離を求めよ。
\({\small (3)}~\)\(\triangle{\rm OAB}\) の面積は \(\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\) となることを示せ。
東京書籍|Advanced数学Ⅱ[701] p.111 練習問題B 10
\({\small (1)}~\)辺 \({\rm OA}\) の長さは、
\(x\) 座標の差が \(|\,x_1-0\,|=|\,x_1\,|\)
\(y\) 座標の差が \(|\,y_1-0\,|=|\,y_1\,|\)
これより、
\(\begin{eqnarray}~~~{\rm OA}&=&\sqrt{x_1^2+y_1^2}\end{eqnarray}\)
したがって、線分 \({\rm OA}\) の長さは \(\sqrt{x_1^2+y_1^2}\)
\({\small (2)}~\)直線 \({\rm OA}\) の方程式を求める。
2点 \({\rm O}(0~,~0)~,~\)\({\rm A}(x_1~,~y_1)\) より、
\(x\) の増加量が \(x_1-0=x_1\)
\(y\) の増加量が \(y_1-0=y_1\)
よって、傾きが \(\displaystyle\frac{\,y_1\,}{\,x_1\,}\)
これより、原点 \({\rm O}(0~,~0)\) を通り傾き \(\displaystyle\frac{\,y_1\,}{\,x_1\,}\) の直線は、
\(\begin{eqnarray}~~~y&=&\displaystyle\frac{\,y_1\,}{\,x_1\,}x
\\[5pt]~x_1y&=&y_1x
\\[3pt]~y_1x-x_1y&=&0\end{eqnarray}\)
よって、点 \({\rm B}(x_2~,~y_2)\) と直線 \({\rm OA}\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,y_1\cdot x_2+(-x_1)\cdot y_2\,|\,}{\,\sqrt{y_1^2+(-x_1)^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}\end{eqnarray}\)
したがって、点 \({\rm B}\) と直線 \({\rm OA}\) の距離は \(\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}\)
\({\small (3)}~\)\(\triangle{\rm OAB}\) の面積は、辺 \({\rm OA}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm OAB}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm OA}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}\sqrt{x_1^2+y_1^2}{\, \small \times \,}\displaystyle\frac{\,|\,x_1y_2-x_2y_1\,|\,}{\,\sqrt{x_1^2+y_1^2}\,}
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\end{eqnarray}\)
したがって、\(\triangle{\rm OAB}\) の面積は \(\displaystyle\frac{\,1\,}{\,2\,}|\,x_1y_2-x_2y_1\,|\) で表される。
問題アーカイブ08
\({\small (1)}~\)辺 \({\rm BC}\) の長さを求めよ。
\({\small (2)}~\)点 \({\rm A}\) と直線 \({\rm BC}\) の距離を求めよ。
\({\small (3)}~\)\(\triangle{\rm ABC}\) の面積を求めよ。
東京書籍|Standard数学Ⅱ[702] p.114 Level Up 6
\({\small (1)}~\)辺 \({\rm BC}\) の長さは、
\(x\) 座標の差が \(|\,3-7\,|=4\)
\(y\) 座標の差が \(|\,5-2\,|=3\)
これより、
\(\begin{eqnarray}~~~{\rm BC}&=&\sqrt{4^2+3^2}
\\[3pt]~~~&=&\sqrt{16+9}
\\[3pt]~~~&=&\sqrt{25}
\\[3pt]~~~&=&5\end{eqnarray}\)
したがって、辺 \({\rm BC}\) の長さは \(5\)
\({\small (2)}~\)直線 \({\rm BC}\) の方程式を求める。
2点 \({\rm B}(7~,~2)~,~\)\({\rm C}(3~,~5)\) より、
\(x\) の増加量が \(3-7=-4\)
\(y\) の増加量が \(5-2=+3\)
よって、傾きが \(\displaystyle\frac{\,+3\,}{\,-4\,}=-\displaystyle\frac{\,3\,}{\,4\,}\)
これより、点 \({\rm B}(7~,~2)\) を通り傾き \(-\displaystyle\frac{\,3\,}{\,4\,}\) の直線は、
\(\begin{eqnarray}~~~y-2&=&-\displaystyle\frac{\,3\,}{\,4\,}(x-7)
\\[5pt]~4(y-2)&=&-3(x-7)
\\[3pt]~4y-8&=&-3x+21
\\[3pt]~~~3x+4y-8-21&=&0
\\[3pt]~3x+4y-29&=&0\end{eqnarray}\)
よって、点 \({\rm A}(1~,~1)\) と直線 \({\rm BC}\) との距離 \(d\) は点と直線との距離の公式より、
\(\begin{eqnarray}~~~d&=&\displaystyle\frac{\,|\,3\cdot1+4\cdot1-29\,|\,}{\,\sqrt{3^2+4^2}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,3+4-29\,|\,}{\,\sqrt{9+16}\,}
\\[5pt]~&=&\displaystyle\frac{\,|\,-22\,|\,}{\,\sqrt{25}\,}
\\[5pt]~&=&\displaystyle\frac{\,22\,}{\,5\,}\end{eqnarray}\)
したがって、点 \({\rm A}\) と直線 \({\rm BC}\) の距離は \(\displaystyle\frac{\,22\,}{\,5\,}\)
\({\small (3)}~\)\(\triangle{\rm ABC}\) の面積は、辺 \({\rm BC}\) を底辺として、高さが \(d\) より、
\(\begin{eqnarray}~~~\triangle{\rm ABC}&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}{\rm BC}{\, \small \times \,}d
\\[5pt]~~~&=&\displaystyle\frac{\,1\,}{\,2\,}{\, \small \times \,}5{\, \small \times \,}\displaystyle\frac{\,22\,}{\,5\,}
\\[5pt]~~~&=&\displaystyle\frac{\,22\,}{\,2\,}=11\end{eqnarray}\)
したがって、\(\triangle{\rm ABC}\) の面積は \(11\)