中心と通る点・直径の両端と円の方程式

中心 \((-3~,~4)\) で原点を通ることより、

---

---

原点 \((0~,~0)\) と中心 \((-3~,~4)\) との距離が半径 \(r\) となるので、

---

\(\begin{eqnarray}~~~r&=&\sqrt{\,(-3)^2+4^2\,}
\\[3pt]~~~&=&\sqrt{\,9+16\,}
\\[3pt]~~~&=&\sqrt{\,25\,}
\\[3pt]~~~&=&5\end{eqnarray}\)

---

よって、中心 \((-3~,~4)\) 、半径 \(5\) の円となるので、

---

\(\begin{eqnarray}~~~\{x-(-3)\}^2+(y-4)^2&=&5^2
\\[3pt]~~~(x+3)^2+(y-4)^2&=&25\end{eqnarray}\)

 
 

2点 \((1~,~-1)\) 、\((3~,~3)\) が直径の両端であることより、

---

---

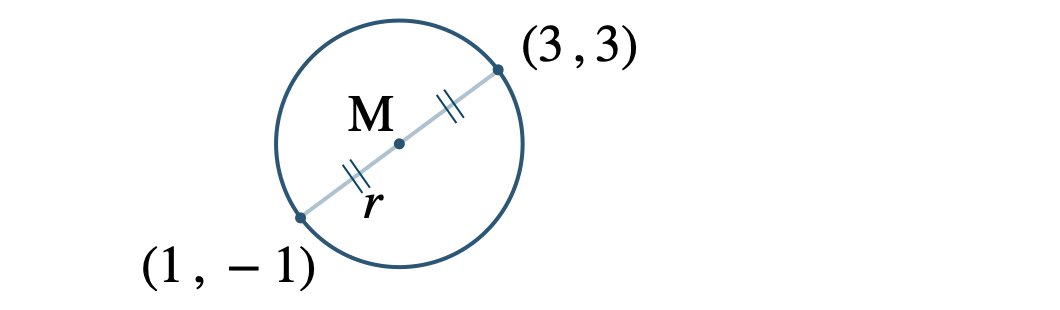
中心は2点を結ぶ線分の中点となるので、

---

\(\begin{eqnarray}~~~&&{\rm M}\left(~\displaystyle\frac{\,1+3\,}{\,2\,}~,~\displaystyle\frac{\,-1+3\,}{\,2\,}~\right)
\\[5pt]~~~&=&{\rm M}\left(~\displaystyle\frac{\,4\,}{\,2\,}~,~\displaystyle\frac{\,2\,}{\,2\,}~\right)
\\[5pt]~~~&=&{\rm M}(2~,~1)\end{eqnarray}\)

---

また、半径 \(r\) は、中心 \((2~,~1)\) と点 \((1~,~-1)\) の距離であるので、

---

　\(x\) 座標の差が \(2-1=1\)
　\(y\) 座標の差が \(1-(-1)=2\)

---

これより、

---

\(\begin{eqnarray}~~~r&=&\sqrt{\,1^2+2^2\,}
\\[3pt]~~~&=&\sqrt{\,1+4\,}
\\[3pt]~~~&=&\sqrt{\,5\,}\end{eqnarray}\)

よって、中心 \((2~,~1)\) 、半径 \(\sqrt{\,5\,}\) の円となるので、

---

\(\begin{eqnarray}~~~(x-2)^2+(y-1)^2&=&(\sqrt{\,5\,})^2
\\[3pt]~~~(x-2)^2+(y-1)^2&=&5\end{eqnarray}\)