軸に接する円の方程式

点 \( (-1~,~2) \) が中心の円が \( x \) 軸と接するとき、

---

---

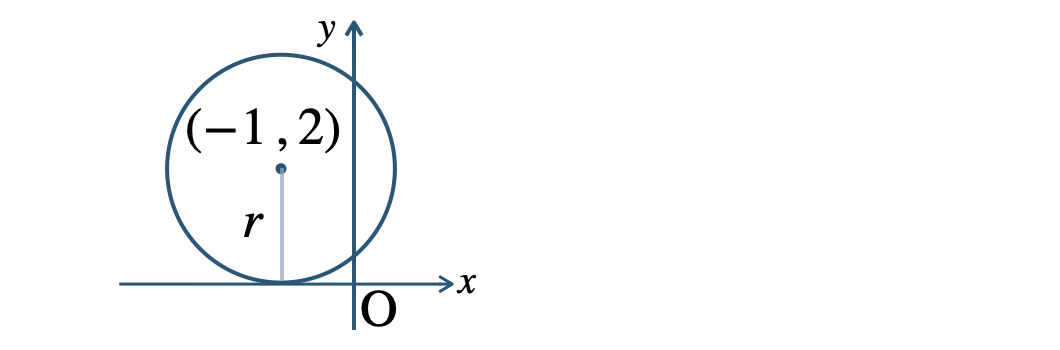
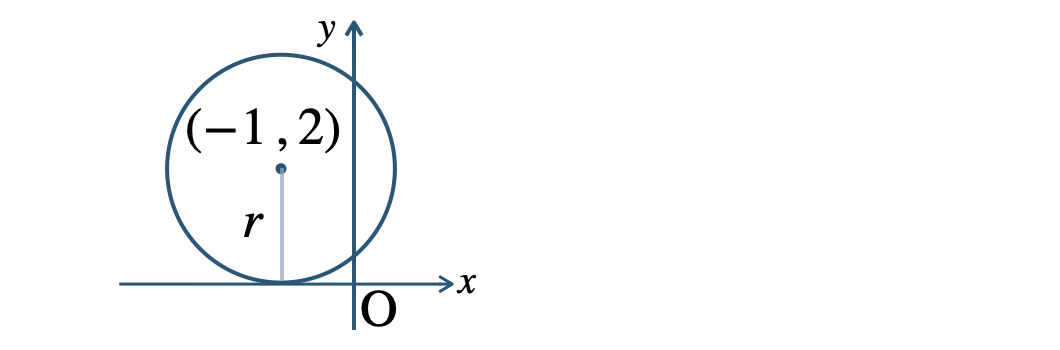
半径 \( r \) は中心の \( y \) 座標の絶対値と等しいので、

---

　\( r=|\,2\,|=2 \)

---

よって、中心 \( (-1~,~2) \)、半径 \( 2 \) の円となるので、

---

\(\begin{eqnarray}~~~\{x-(-1)\}^2+(y-2)^2&=&2^2
\\[3pt]~~~(x+1)^2+(y-2)^2&=&4\end{eqnarray}\)

 
 

点 \( (-1~,~2) \) が中心の円が \( y \) 軸と接するとき、

---

---

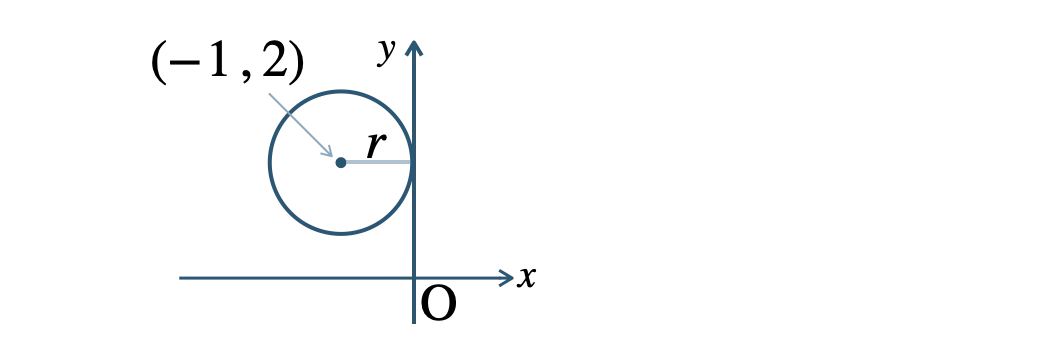
半径 \( r \) は中心の \( x \) 座標の絶対値と等しいので、

---

　\( r=|\,-1\,|=1 \)

---

よって、中心 \( (-1~,~2) \)、半径 \( 1 \) の円となるので、

---

\(\begin{eqnarray}~~~\{x-(-1)\}^2+(y-2)^2&=&1^2
\\[3pt]~~~(x+1)^2+(y-2)^2&=&1\end{eqnarray}\)

 
 

\( x \) 軸と \( y \) 軸の両方に接して、点 \( (2~,~-1) \) を通るので、

---

---

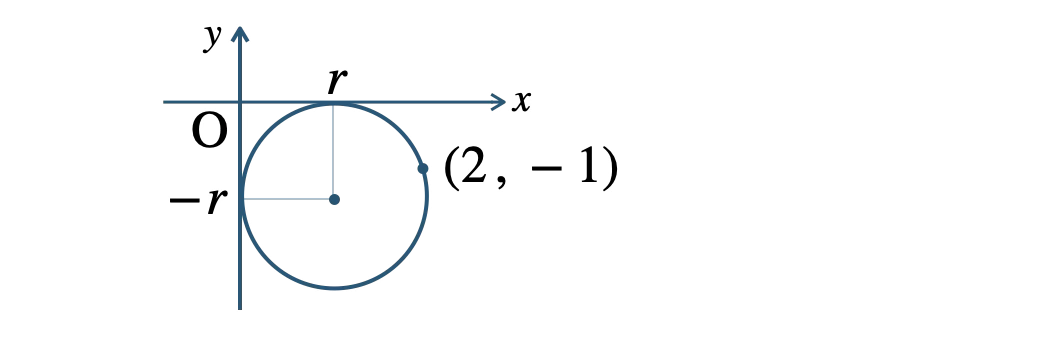
円は、第4象限にあり、半径を \( r~(r \gt 0) \) とすると、中心の \( x \) 座標は \( r \)、\( y \) 座標は \( -r \) となる

---

よって、中心 \( (r~,~-r) \)、半径 \( r \) の円の方程式は、

---

\(\begin{eqnarray}~~~(x-r)^2+\{y-(-r)\}^2&=&r^2
\\[3pt]~~~(x-r)^2+(y+r)^2&=&r^2~~~\cdots~{\small [\,1\,]}\end{eqnarray}\)

---

\( {\small [\,1\,]} \) は \( (2~,~-1) \) を通るので、

---

\(\begin{eqnarray}~~~(2-r)^2+(-1+r)^2&=&r^2
\\[3pt]~~~4-4r+r^2+1-2r+r^2&=&r^2
\\[3pt]~~~r^2-6r+5&=&0
\\[3pt]~~~(r-1)(r-5)&=&0
\\[3pt]~~~r&=&1~,~5\end{eqnarray}\)

---

　\( r=1 \) のとき、\( {\small [\,1\,]} \) より、

---

　　\( (x-1)^2+(y+1)^2=1^2 \)

---

　\( r=5 \) のとき、\( {\small [\,1\,]} \) より、

---

　　\( (x-5)^2+(y+5)^2=5^2 \)

---

したがって、

---

\(\begin{eqnarray}~~~(x-1)^2+(y+1)^2&=&1
\\[3pt]~~~(x-5)^2+(y+5)^2&=&25\end{eqnarray}\)